鲁教版（五四制）2022-2023学年度第二学期六年级数学 线段、射线、直线 期中复习
试卷更新日期：2023-04-17 类型：复习试卷
一、单选题
-
1. 如图，下列说法错误的是（ ）
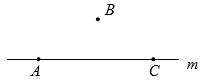A、点在直线上，点在直线外 B、射线与射线不是同一条射线 C、直线还可以表示为直线或直线 D、图中有直线3条，射线2条，线段1条2. 下列各线段的表示方法中，正确的是（ ）A、线段A B、线段ab C、线段AB D、线段Ab3. 将一根木条固定在墙上至少需要两枚钉子，这一生活经验运用到的数学知识是（ ）
A、两点确定一条直线 B、两点之间线段最短 C、在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线 D、连结直线外一点与直线上各点的所有连线中，垂线段最短4. 如图，C、D两点在线段AB上，则图中共有线段（ ）条．
A、3 B、4 C、5 D、65. 下列说法不正确的个数有（ ）①经过两点有一条直线，且只有一条直线；②常数项的同类项还是常数项；
③a+b= a-(-b)；④连接两点间的线段，叫做这两点的距离；
⑤如果线段AB=BC，则点B是线段AC的中点．
A、2个 B、3个 C、4个 D、5个6. 经过刨平的木板上的两点，能弹出一条笔直的墨线，且只能弹出一条这样的墨线，理由是（ ）
A、两点确定一条直线 B、两点之间线段最短 C、连结直线外一点与直线上各点的所有线段中，垂线段最短 D、在同一平面内，过一点有一条而且仅有一条直线垂直于已知直线7. 在下列生活、生产现象中，可以用基本事实“两点之间，线段最短”来解释的是（ ）①用两颗钉子就可以把木条固定在墙上；②在A、B两地之间架设电线时，总是尽可能沿线段AB架设；③植树时，只要栽下两棵树，就可以把同一行树栽在同一条直线上；④把弯曲的公路改直，就能缩短路程.
A、①② B、①③ C、②④ D、③④8. 如图，C，D在线段上，下列四个说法：①直线上以B，C，D，E为端点的线段共有6条；
②图中有3对互为补角的角；
③若 ， ， 则以A为顶点的所有小于平角的角的度数和为370°；
④若 ， ， ， 点F是线段上任意一点（包含端点），则点F到点B，C，D，E的距离之和的最小值为15，最大值为25
其中正确说法的个数是（ ）
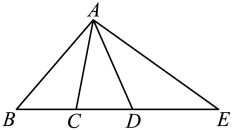A、1个 B、2个 C、3个 D、4个9. 下列说法：①过两点有且只有一条直线；②连接两点的线段叫做两点间的距离；③两点之间，线段最短；④若α＝29°45′，则α的补角是150°55′；⑤若AB＝BC，则点B是线段AC的中点．其中正确的有（ ）A、1个 B、2个 C、3个 D、4个10. 下列说法中正确的是（ ）A、射线和射线是同一条射线 B、延长线段和延长线段的含义是相同的 C、若 ， ， 三点在同一直线上，且 ， 则点是线段的中点 D、若 ， ， ， 则有二、填空题
-
11. 要在墙上订牢一根木条，至少需要2颗钉子，其理由是 ．12. 如图，点 ， ， ， ， 在线段上，则图中共有条线段．
13. 班长小明在墙上钉木条挂报夹，钉一颗钉时，木条还任意转动，钉两颗钉时，木条再也不动了，用数学知识解释这种现象为：.14. 如图，数学知识在生产和生活中被广泛应用．下列实例所应用的最主要的几何知识为：①射击时，瞄准星的缺口、准星和射击目标在同一直线上，应用了“两点确定一条直线”；
②车轮做成圆形，应用了“圆上各点到圆心的距离相等”；
③学校门口的伸缩门由菱形而不是其他四边形组成，应用了“菱形的对角线互相垂直平分”；
④地板砖可以做成矩形，应用了“矩形对边相等”．
上述说法正确的是 ． （填序号）
15. 同一平面内的四个点最多能确定条直线三、解答题
-
16. 请按下列语句画出图形，并写出线段的长度：
线段 ， 点在的延长线上， ， 是的中点．
17. 如图，已知线段a，b，用尺规作一条线段 ， 使 ．
18. 已知线段AB=15cm，点C在线段AB上， ，D为BC的中点，求线段AD的长.四、综合题
-
19. 如图，已知直线 ， 射线 ， 线段.
(1)、用无刻度的直尺和圆规作图：延长到点D，使 ， 连接.(2)、比较与的大小，并说明理由.20. 如图，平面上有三个点A，B，C．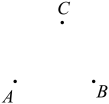
(1)、根据下列语句按要求画图．①画直线 ， 画射线 ， 连接；
②用圆规在线段的延长线上截取 ， 连接（保留作图痕迹）；
(2)、（填“>”“=”或“<”），依据是 ．
