2023年江苏省南京市中考数学二模试题
试卷更新日期:2023-04-17 类型:中考模拟
一、单选题(每题2分,共12分)
-
1. 据国家统计局统计,2022年中国超120万亿元,比上年增长 , 将120万亿用科学记数法表示为( )A、 B、 C、 D、2. 下列各式正确的是( )A、a4•a5=a20 B、a2+2a3=2a5 C、a4÷a=a3 D、(-a2b3)2=a4b93. 长度分别为10,8,8,6的四根细木棒首尾相连,围成一个三角形(木棒全都用上且允许连接,但不允许折断),得到的三角形的最长边长为( )A、10 B、14 C、16 D、184. 上周五某股民小王买进某公司股票1000股,每股35元,下表为本周内每日股票的涨跌情况(单位:元):
星期
一
二
三
四
五
每股涨跌
则在本周五收盘时,每股的价格是( )
A、34元 B、35元 C、36元 D、37元5. 下列各式中,正确的是( )A、±=±2 B、=±2 C、=﹣2 D、﹣=26. 如图将绕点旋转得到 , 设点的坐标为 , 则A的坐标为( )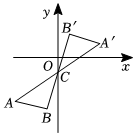 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题2分,共20分)
-
7. 若二次根式意义,则x可以是(写出一个x的值即可).8. 已知a,b互为相反数,则代数式的值为 .
若 , 则b= .
9. 计算: .10. 方程和方程所有实数根之积为.11. 已知三条中位线的长分别为3、4、5,则该三角形的面积为.12. 如图,矩形的面积为36,对角线与双曲线相交于点 , 且 , 则的值为. 13. 如图正八边形ABCDEFGH中,延长对角线BF与边DE交于点M,则°.
13. 如图正八边形ABCDEFGH中,延长对角线BF与边DE交于点M,则°. 14. 如图,AB是半圆的直径,C为半圆上一点,BC,D为弧BC上一点.连接OD,连接AE,若四边形ACDE为平行四边形,AE=2 , 则AB的长为.
14. 如图,AB是半圆的直径,C为半圆上一点,BC,D为弧BC上一点.连接OD,连接AE,若四边形ACDE为平行四边形,AE=2 , 则AB的长为. 15. 如图,已知在矩形中, , , 将矩形绕点C旋转,使点B恰好落在对角线上的点处,点A、D分别落在点、处,边、分别与边交于点M、N,那么线段的长为 .
15. 如图,已知在矩形中, , , 将矩形绕点C旋转,使点B恰好落在对角线上的点处,点A、D分别落在点、处,边、分别与边交于点M、N,那么线段的长为 . 16. 已知点 , 的半径为1,OA切于点A,点P为上的动点,连接OP,AP,若是等腰三角形,则点P的坐标为 .
16. 已知点 , 的半径为1,OA切于点A,点P为上的动点,连接OP,AP,若是等腰三角形,则点P的坐标为 .
三、解答题(共8题,共61分)
-
17. 解不等式组并把解集在数轴上表示出来.18. 为弘扬勤俭美德,落实节约政策,某旅游景点进行设施改造,将手动水龙头全部换成感应水龙头.已知改造完成后,平均每天的用水量减少 , 48吨水可以比原来多用6天,该景点在实施改造后平均每天用水多少吨?19. 先化简,再求值:
, 其中满足 , 取一个整数即可.
20. 如图,等腰直角三角板如图放置.直角顶点C在直线m上,分别过点A、B作AE⊥直线m于点E,BD⊥直线m于点D.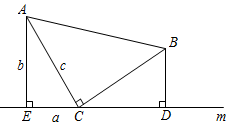
①求证: ;
②若设△AEC三边分别为a、b、c,利用此图证明勾股定理.
21. 某校为了了解全校400名学生参加课外锻炼的情况,随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查,结果如下:(单位:分)40 21 35 24 40 38 23 52 35 62 36 15 51 45 40 42 40 32 43 36 34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45
(1)、补全频率分布表和频率分布直方图.分组
频数
频率
4.5﹣22.5
2
0.050
22.5﹣30.5
3
30.5﹣38.5
10
0.250
38.5﹣46.5
19
46.5﹣54.5
5
0.125
54.5﹣62.5
1
0.025
合计
40
1.000
 (2)、填空:在这个问题中,总体是 , 样本是 . 由统计结果分析的,这组数据的平均数是38.35(分),众数是 , 中位数是 .(3)、如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况,你认为用平均数、众数、中位数中的哪一个量比较合适?(4)、估计这所学校有多少名学生,平均每天参加课外锻炼的时间多于30分?22. 初三某班举办了一场摸牌游戏,由甲、乙两名同学进行.现有5张背面完全相同的牌,正面分别标有数字-1,2,3,5,6,将五张牌背面朝上,洗匀后放在桌子上,甲从中随机抽取一张牌后放回,乙再随机抽取一张牌.(1)、请用列表或画树状图的方法,求两人抽取的数字相同的概率.(2)、若两人抽取的数字差的绝对值等于1,则甲获胜;若抽取的数字差的绝对值小于1,则乙获胜,这个游戏公平吗?请用概率的知识加以解释.23. 等腰△ABC中,AB=AC,以AB为直径作圆交BC于点D,请仅用无刻度的直尺,根据下列条件分别在图1、图2中画一条弦,使这条弦的长度等于弦BD.(保留作图痕迹,不写作法)
(2)、填空:在这个问题中,总体是 , 样本是 . 由统计结果分析的,这组数据的平均数是38.35(分),众数是 , 中位数是 .(3)、如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况,你认为用平均数、众数、中位数中的哪一个量比较合适?(4)、估计这所学校有多少名学生,平均每天参加课外锻炼的时间多于30分?22. 初三某班举办了一场摸牌游戏,由甲、乙两名同学进行.现有5张背面完全相同的牌,正面分别标有数字-1,2,3,5,6,将五张牌背面朝上,洗匀后放在桌子上,甲从中随机抽取一张牌后放回,乙再随机抽取一张牌.(1)、请用列表或画树状图的方法,求两人抽取的数字相同的概率.(2)、若两人抽取的数字差的绝对值等于1,则甲获胜;若抽取的数字差的绝对值小于1,则乙获胜,这个游戏公平吗?请用概率的知识加以解释.23. 等腰△ABC中,AB=AC,以AB为直径作圆交BC于点D,请仅用无刻度的直尺,根据下列条件分别在图1、图2中画一条弦,使这条弦的长度等于弦BD.(保留作图痕迹,不写作法)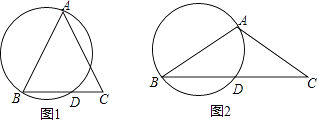 (1)、如图1,∠A<90°;(2)、如图2,∠A>90°.24. 如图1的风力发电机,风轮的三个叶片均匀分布,当风轮的叶片在风力作用下旋转时,最高点距地面 , 最低点距地面 . 如图2是该风力发电机的示意图,发电机的塔身垂直于水平地面(点 , , , , , , 在同一平面内).
(1)、如图1,∠A<90°;(2)、如图2,∠A>90°.24. 如图1的风力发电机,风轮的三个叶片均匀分布,当风轮的叶片在风力作用下旋转时,最高点距地面 , 最低点距地面 . 如图2是该风力发电机的示意图,发电机的塔身垂直于水平地面(点 , , , , , , 在同一平面内). (1)、求风轮叶片的长度;(2)、如图2,点在右侧,且 . 求此时风叶的端点距地面的高度.(参考数据: , )
(1)、求风轮叶片的长度;(2)、如图2,点在右侧,且 . 求此时风叶的端点距地面的高度.(参考数据: , )四、综合题(共3题,共27分)
-
25. 【概念学习】
现规定:求若干个相同的有理数(均不等于0)的商的运算叫做除方,比如2÷2÷2,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)等,类比有理数的乘方,我们把2÷2÷2写作2③ , 读作“2的圈3次方”,(﹣3)÷(﹣3)÷(﹣3)÷(﹣3)写作(﹣3)④ , 读作“(﹣3)的圈4次方”,一般地,把(a≠0)写作aⓝ , 读作“a的圈n次方”.
(1)、【初步探究】
直接写出计算结果:2③= , (﹣)④=;(2)、下列关于除方说法中,错误的是: .A、任何非零数的圈2次方都等于1 B、对于任何正整数n,1ⓝ=1 C、3④=4③ D、负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数(3)、【深入思考】我们知道,有理数的减法运算可以转化为加法运算,除法运算可以转化为乘法运算,有理数的除方运算如何转化为乘方运算呢?
试一试:仿照上面的算式,把下列除方运算直接写成幂的形式:(﹣3)⑤= , ()⑥=. (4)、想一想:请把有理数a(a≠0)的圈n(n≥3)次方写成幂的形式为aⓝ=.(5)、算一算:=.26. 已知抛物线的图象经过坐标原点O.(1)、求抛物线解析式.(2)、若B,C是抛物线上两动点,直线恒过点 , 设直线为 , 直线为 .
(4)、想一想:请把有理数a(a≠0)的圈n(n≥3)次方写成幂的形式为aⓝ=.(5)、算一算:=.26. 已知抛物线的图象经过坐标原点O.(1)、求抛物线解析式.(2)、若B,C是抛物线上两动点,直线恒过点 , 设直线为 , 直线为 .①若B、C两点关于y轴对称,求的值.
②求证:无论k为何值,为定值.
27. 某数学课外活动小组在学习了勾股定理之后,针对图1中所示的“由直角三角形三边向外侧作多边形,它们的面积 之间的关系问题”进行了以下探究: (1)、(类比探究)
(1)、(类比探究)如图2,在 中, 为斜边,分别以 为斜边向外侧作 ,若 ,则面积 之间的关系式为;
(2)、(推广验证)如图3,在 中, 为斜边,分别以 为边向外侧作任意 ,满足 ,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论:若不成立,请说明理由;
(3)、(拓展应用)如图4, 中, ,分别以它的三边向外作平行四边形, 交 于 交 于 ,且 ,若平行四边形 和平行四边形 的面积分别为 和 ,则平行四边形 的面积为;
 (4)、如图5,在五边形 中, ,点 在 上, ,求五边形 的面积为;
(4)、如图5,在五边形 中, ,点 在 上, ,求五边形 的面积为;