中考数学优生特训:图形变换
试卷更新日期:2023-04-16 类型:二轮复习
一、单选题
-
1. 如图是一张矩形纸片 , 点 , 分别在边 , 上, , .把该纸片沿折叠,若点 , 的对应点分别为 , , 的延长线过点 , 则的值为( )
 A、 B、 C、 D、42. 如图是一张矩形纸片 , 点E是中点,点F在上,把该纸片沿折叠,点A、B的对应点分别为、 , 与相交于点G,的延长线经过点C.若 , 则的值为( )
A、 B、 C、 D、42. 如图是一张矩形纸片 , 点E是中点,点F在上,把该纸片沿折叠,点A、B的对应点分别为、 , 与相交于点G,的延长线经过点C.若 , 则的值为( )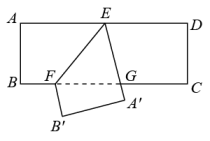 A、 B、 C、 D、3. 如图,将矩形ABCD沿着GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,点E,O,F 在另一条直线上. 以下结论正确的是( )
A、 B、 C、 D、3. 如图,将矩形ABCD沿着GE,EC,GF翻折,使得点A,B,D恰好都落在点O处,且点G,O,C在同一条直线上,点E,O,F 在另一条直线上. 以下结论正确的是( )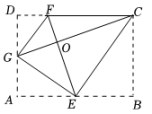 A、△COF∽△CEG B、OC=3OF C、AB:AD=4:3 D、GE=DF4. 在正方形ABCD中,AB=3,点E在边CD上,且DE=1,将△ADE沿AE对折到△AFE,延长EF交边BC于点G,连接AG,CF.下列结论,其中正确的有( )个.
A、△COF∽△CEG B、OC=3OF C、AB:AD=4:3 D、GE=DF4. 在正方形ABCD中,AB=3,点E在边CD上,且DE=1,将△ADE沿AE对折到△AFE,延长EF交边BC于点G,连接AG,CF.下列结论,其中正确的有( )个.

(1)CG=FG;(2)∠EAG=45°;(3)S△EFC=;(4)CF=GEA、1个 B、2个 C、3个 D、4个5. 如图,过边长为2的等边的顶点C作直线 , 然后作关于直线l对称的 , P为线段上一动点,连接 , , 则的最小值是( ) A、4 B、3 C、2 D、16. 如图,是边长为2的等边三角形,的面积等于 , D,E分别为 , 的中点,P是上的一个动点,则的最小值为( )
A、4 B、3 C、2 D、16. 如图,是边长为2的等边三角形,的面积等于 , D,E分别为 , 的中点,P是上的一个动点,则的最小值为( ) A、 B、 C、1 D、27. 如图,在平面直角坐标系中,将边长为a的正方形OABC绕点O顺时针旋转后得到正方形 , 依此方式连续旋转2023次得到正方形 , 那么点的坐标是( )
A、 B、 C、1 D、27. 如图,在平面直角坐标系中,将边长为a的正方形OABC绕点O顺时针旋转后得到正方形 , 依此方式连续旋转2023次得到正方形 , 那么点的坐标是( ) A、(a,a) B、 C、 D、8. 如图所示,正方形 , , 内接于五边形 , 该五边形是轴对称图形,与为对称边, , , 则的值是( )
A、(a,a) B、 C、 D、8. 如图所示,正方形 , , 内接于五边形 , 该五边形是轴对称图形,与为对称边, , , 则的值是( ) A、 B、 C、 D、9. 如图,将矩形纸片 分别沿 、 折叠,若B、D两点恰好都落在对角线的交点O上,下列说法:①四边形 为菱形,② ,③若 ,则四边形 的面积为 ,④ ,其中正确的说法有( )个.
A、 B、 C、 D、9. 如图,将矩形纸片 分别沿 、 折叠,若B、D两点恰好都落在对角线的交点O上,下列说法:①四边形 为菱形,② ,③若 ,则四边形 的面积为 ,④ ,其中正确的说法有( )个. A、4 B、3 C、2 D、110. 如图,在正方形ABCD中, ,点M在CD边上,且 , 与 关于AM所在的直线对称,延长CB到点F,使得 ,分别连接AF,EF,则线段EF的长为( ).
A、4 B、3 C、2 D、110. 如图,在正方形ABCD中, ,点M在CD边上,且 , 与 关于AM所在的直线对称,延长CB到点F,使得 ,分别连接AF,EF,则线段EF的长为( ). A、 B、 C、 D、11. 如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在点 , 处,且经过点B,EF为折痕,当⊥CD时,的值为( )
A、 B、 C、 D、11. 如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A,D分别落在点 , 处,且经过点B,EF为折痕,当⊥CD时,的值为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
12. 如图,在中, , , D为线段的中点,点E,F分别在 , 上, , 且 , 沿将折叠得到 , 若 , 则的长是 .
 13. 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.则下列结论:①CE=CF;②线段EF的最小值为;③若点F恰好落在弧BC上,则AD=④当AD=2时,与半圆相切;⑤当点D从点A运动到点B时,线段 EF扫过的面积是。其中正确结论的序号是。
13. 如图,点C在以AB为直径的半圆上,AB=8,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.则下列结论:①CE=CF;②线段EF的最小值为;③若点F恰好落在弧BC上,则AD=④当AD=2时,与半圆相切;⑤当点D从点A运动到点B时,线段 EF扫过的面积是。其中正确结论的序号是。 14. 何老师在一次“探析矩形折叠问题”的公开课上,与同学们一起对折纸进行了如下探究:已知正方形边长为1,G是边的中点,E是射线上的一个动点.
14. 何老师在一次“探析矩形折叠问题”的公开课上,与同学们一起对折纸进行了如下探究:已知正方形边长为1,G是边的中点,E是射线上的一个动点. (1)、如图① ,若点E在线段上且点E与点C不重合,连结 , 将沿着翻折,使点C落在上的点M处,连结延长交边于点F且 , 则的值为(2)、若点E与点C不重合,以点C为圆心,线段的长为半径作 , 当与线段只有一个公共点时,的取值范围是.15. 如图,已知正方形的边长为1,点M是边的中点,将沿直线翻折,使得点C落在同一平面内的点E处,联结并延长交射线于点F,那么的长为 .
(1)、如图① ,若点E在线段上且点E与点C不重合,连结 , 将沿着翻折,使点C落在上的点M处,连结延长交边于点F且 , 则的值为(2)、若点E与点C不重合,以点C为圆心,线段的长为半径作 , 当与线段只有一个公共点时,的取值范围是.15. 如图,已知正方形的边长为1,点M是边的中点,将沿直线翻折,使得点C落在同一平面内的点E处,联结并延长交射线于点F,那么的长为 . 16. 如图,在矩形中, , , 点为线段的中点,动点从点出发,沿的方向在和上运动,将矩形沿折叠,点的对应点为 , 当点恰好落在矩形的对角线上时,点运动的距离为.
16. 如图,在矩形中, , , 点为线段的中点,动点从点出发,沿的方向在和上运动,将矩形沿折叠,点的对应点为 , 当点恰好落在矩形的对角线上时,点运动的距离为.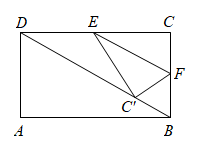 17. 如图,已知,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y=(k>0)的图象与AC边交于点E,将△CEF沿EF对折后,C点恰好落在OB上的点D处,则k的值为 .
17. 如图,已知,在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y=(k>0)的图象与AC边交于点E,将△CEF沿EF对折后,C点恰好落在OB上的点D处,则k的值为 .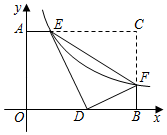 18. 如图,正方形ABCD,AB=2,点E为AD上一动点,将三角形ABE沿BE折叠,点A落在点F处,连接DF并延长,与边AB交于点G,若点G为AB中点,则AE= .
18. 如图,正方形ABCD,AB=2,点E为AD上一动点,将三角形ABE沿BE折叠,点A落在点F处,连接DF并延长,与边AB交于点G,若点G为AB中点,则AE= . 19. 如图,等腰三角形的底边长为 , 面积是 , 腰的垂直平分线分别交 , 边于点 , , 若点为边的中点,点为线段上一动点,则周长的最小值为 .
19. 如图,等腰三角形的底边长为 , 面积是 , 腰的垂直平分线分别交 , 边于点 , , 若点为边的中点,点为线段上一动点,则周长的最小值为 . 20. 如图1,在长方形ABCD中,E点在AD上,并且∠ABE=26˚,分别以BE、CE为折痕进行折叠压平,如图2,若图2中∠AED=n°,则∠DEC的度数为 .
20. 如图1,在长方形ABCD中,E点在AD上,并且∠ABE=26˚,分别以BE、CE为折痕进行折叠压平,如图2,若图2中∠AED=n°,则∠DEC的度数为 .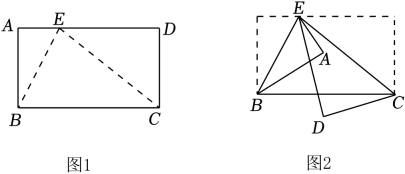 21. 如图,一次函数y=-x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为.
21. 如图,一次函数y=-x+3的图象与x轴交于点A,与y轴交于点B,C是x轴上一动点,连接BC,将△ABC沿BC所在的直线折叠,当点A落在y轴上时,点C的坐标为.
三、解答题
-
22. 古希腊有一个著名的“将军饮马问题”,大致内容如下:古希腊一位将军,每天都要巡查河岸同侧的两个军营A , B . 他总是先去A营,再到河边饮马,之后,再巡查B营.他时常想,怎么走,才能使他每天走的路程之和最短呢?大数学家海伦曾用轴对称的方法巧妙地解决了这个问题.
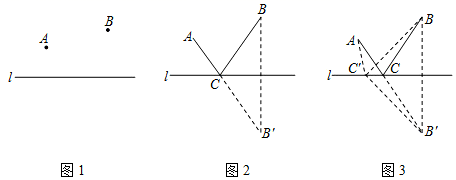
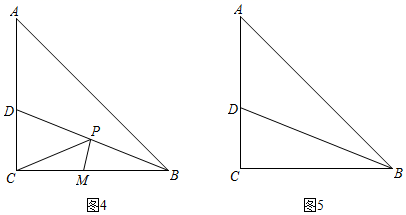
如图2,作B关于直线l的对称点B′,连结AB′与直线l交于点C , 点C就是所求的位置.
证明:如图3,在直线l上另取任一点C′,连结AC′,BC , B′C′,
∵直线l是点B , B′的对称轴,点C , C′在l上,
∴CB= ▲ , C′B= ▲ ,
∴AC +CB=AC+CB′= ▲ .
在△AC′B′,
∵AB′<AC′+C′B′,
∴AC+CB<AC′+C′B′即AC+CB最小.
本问题实际上是利用轴对称变换的思想,把A , B在直线同侧的问题转化为在直线的两侧,从而可利用“两点之间线段最短”,即“三角形两边之和大于第三边”的问题加以解决(其中C在AB′与l的交点上,即A , C , B′三点共线).本问题可归纳为“求定直线上一动点与直线外两定点的距离和的最小值”的问题的数学模型.
拓展应用:如图,等腰直角△ABC中,∠ACB = 90°,BD平分∠ABC交AC于D , 点P是BD上一个动点,点M是BC上一个动点,请在图5中画出PC + PM的值最小时P的位置.(可用三角尺)
23. 已知一个等边三角形纸片 ,将该纸片放置在平面直角坐标系中, 为坐标原点,使边 与 轴的正半轴重合,点 落在第一象限,过点 作 垂直于 轴,垂足为点 .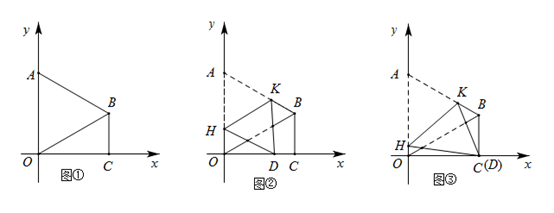
(Ⅰ)如图①,若点 坐标为 ,求 的长;
(Ⅱ)如图②,将四边形 折叠,使点 落在线段 上的点为点 , 为折痕,点 在 上,点 在 上,且使 轴.
①试判断四边形 的形状,并证明你的结论;
②求 的值;
(Ⅲ)如图③,将四边形 折叠,使点 落在线段 上的点 与 点重合, 为折痕,点 在 上,点 在 上,求 的值(直接写出结果即可).
24. 在平面直角坐标系中,已知O为坐标原点,点 ,以点A为旋转中心,把顺时针旋转,得.
(Ⅰ)如图①,当旋转后满足 轴时,求点C的坐标.
(Ⅱ)如图②,当旋转后点C恰好落在x轴正半轴上时,求点D的坐标.
(Ⅲ)在(Ⅱ)的条件下,边 上的一点P旋转后的对应点为 ,当 取得最小值时,求点P的坐标(直接写出结果即可)
25. 如图1,将矩形 沿 折叠,使顶点 落在 上的点 处,然后将矩形展平.如图2,将矩形 沿 折叠,使顶点 落在折痕 上的点 处,再将矩形 沿 折叠,此时顶点 恰好落在 上的点 处.
求证:
26. 如图,一个三角形的纸片ABC , 其中∠A=∠C .
①把△ABC纸片按(如图1)所示折叠,使点A落在BC边上的点F处,DE是折痕.说明BC//DF;
②把△ABC纸片沿DE折叠,当点A落在四边形BCED内时(如图2),探索∠C与∠1+∠2之间的大小关系,并说明理由;
③当点A落在四边形BCED外时(如图3),∠C与∠1、∠2的关系是 . (直接写出结论)
四、综合题
-
27. 如图,在中,∠C=90°,∠A=30°,BC=12cm.动点P从点A出发,沿AB向点B运动,动点Q从点B出发,沿BC向点C运动,如果动点P以2cm/s,Q以1cm/s的速度同时出发,设运动时间为t(s),解答下列问题:
 (1)、t为多少时,是等边三角形?(2)、P、Q在运动过程中,的形状不断发生变化,当t为多少时,是直角三角形?请说明理由.28. 如图,中, , , .点为斜边的中点, , 交边于点.点为射线上的动点,点为边上的动点,且运动过程中始终保持.
(1)、t为多少时,是等边三角形?(2)、P、Q在运动过程中,的形状不断发生变化,当t为多少时,是直角三角形?请说明理由.28. 如图,中, , , .点为斜边的中点, , 交边于点.点为射线上的动点,点为边上的动点,且运动过程中始终保持. (1)、求证:;(2)、设 , .求关于的函数解析式,并写出该函数的定义域;(3)、联结 , 交线段于点 , 当为等腰三角形时,求线段的长.29. 如图,在∠DAM内部作Rt△ABC,AB平分∠DAM,∠ACB=90°,AB=10,AC=8,点N为BC的中点,动点E由A点出发,沿AB运动,速度为每秒5个单位,动点F由A点出发,沿AM运动,速度为每秒8个单位,当点E到达点B时,两点同时停止运动,过A、E、F作⊙O.
(1)、求证:;(2)、设 , .求关于的函数解析式,并写出该函数的定义域;(3)、联结 , 交线段于点 , 当为等腰三角形时,求线段的长.29. 如图,在∠DAM内部作Rt△ABC,AB平分∠DAM,∠ACB=90°,AB=10,AC=8,点N为BC的中点,动点E由A点出发,沿AB运动,速度为每秒5个单位,动点F由A点出发,沿AM运动,速度为每秒8个单位,当点E到达点B时,两点同时停止运动,过A、E、F作⊙O. (1)、判断△AEF的形状为 , 并判断AD与⊙O的位置关系为;(2)、求t为何值时,EN与⊙O相切,求出此时⊙O的半径,并比较半径与劣弧长度的大小;(3)、直接写出△AEF的内心运动的路径长为;(注:当A、E、F重合时,内心就是A点)(4)、直接写出线段EN与⊙O有两个公共点时,t的取值范围为 .
(1)、判断△AEF的形状为 , 并判断AD与⊙O的位置关系为;(2)、求t为何值时,EN与⊙O相切,求出此时⊙O的半径,并比较半径与劣弧长度的大小;(3)、直接写出△AEF的内心运动的路径长为;(注:当A、E、F重合时,内心就是A点)(4)、直接写出线段EN与⊙O有两个公共点时,t的取值范围为 .(参考数据:sin37°= , tan37°= , tan74°≈ , sin74°≈ , cos74°≈)
30. 如图1,抛物线y=ax2+bx+3与x轴交于点A(3,0)、B(﹣1,0),与y轴交于点C,点P为抛物线第一象限上的动点,点F为y轴上的动点,连结PA,PF,AF.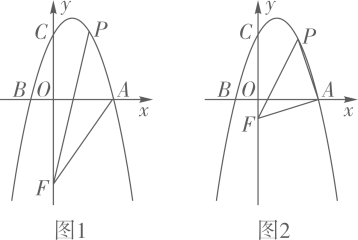 (1)、求该抛物线所对应的函数表达式;(2)、如图1,当点F的坐标为(0,﹣4),求出此时△AFP面积的最大值;(3)、如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.31. 在矩形ABCD中, , 动点P从A出发,以1个单位每秒速度,沿射线AB方向运动,同时,动点Q从点C出发,以2个单位每秒速度,沿射线BC方向运动,设运动时间为t秒,连结DP,DQ.
(1)、求该抛物线所对应的函数表达式;(2)、如图1,当点F的坐标为(0,﹣4),求出此时△AFP面积的最大值;(3)、如图2,是否存在点F,使得△AFP是以AP为腰的等腰直角三角形?若存在,求出所有点F的坐标;若不存在,请说明理由.31. 在矩形ABCD中, , 动点P从A出发,以1个单位每秒速度,沿射线AB方向运动,同时,动点Q从点C出发,以2个单位每秒速度,沿射线BC方向运动,设运动时间为t秒,连结DP,DQ. (1)、如图1.证明: .(2)、作平分线交直线BC于点E;
(1)、如图1.证明: .(2)、作平分线交直线BC于点E;①图2,当点E与点B重合时,求t的值.
②连结PE,PQ,当与相似时,求t的值.
32. 已知:如图1:在中, , , , 在下方作于点D, , 动点E从点A开始沿边以的速度运动,动点F从点C开始沿边以的速度运动.点E和点F同时出发,当点E到达点C时,点F也随之停止运动.设动点E的运动时间为 , 解答下列问题: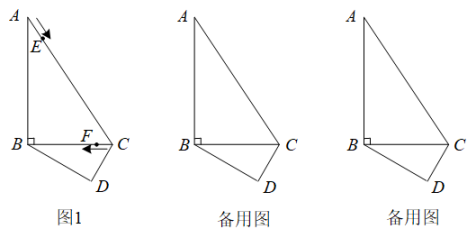 (1)、连接 , 当t为何值时,点C在线段的垂直平分线上;(2)、在运动过程中,是否存在某一时刻t,使是直角三角形?若存在,求出t的值;若不存在,请说明理由;(3)、在(2)的条件下,请直接写出的面积.33. 动点问题是数学学习中常见的问题,解决此类问题的关键是动中求静,运用分类讨论及数形结合的思想灵活解决问题.如图,在等边三角形中, , 点在线段上从点B出发向点A运动(点不与点重合),点运动的速度为;点在线段上从点出发向点B运动(点不与点B重合),点运动的速度为 , 设点 , 同时运动,运动时间为 .
(1)、连接 , 当t为何值时,点C在线段的垂直平分线上;(2)、在运动过程中,是否存在某一时刻t,使是直角三角形?若存在,求出t的值;若不存在,请说明理由;(3)、在(2)的条件下,请直接写出的面积.33. 动点问题是数学学习中常见的问题,解决此类问题的关键是动中求静,运用分类讨论及数形结合的思想灵活解决问题.如图,在等边三角形中, , 点在线段上从点B出发向点A运动(点不与点重合),点运动的速度为;点在线段上从点出发向点B运动(点不与点B重合),点运动的速度为 , 设点 , 同时运动,运动时间为 . (1)、在点 , 运动过程中,经过几秒时为等边三角形?(2)、在点 , 运动过程中,若某时刻为直角三角形,请计算运动时间 .
(1)、在点 , 运动过程中,经过几秒时为等边三角形?(2)、在点 , 运动过程中,若某时刻为直角三角形,请计算运动时间 .