备考2023年中考数学嘉兴卷变式阶梯训练：第23题

试卷更新日期：2023-04-15 类型：三轮冲刺

进入出卷网下载

一、原题

1. 已知抛物线L₁：y＝a(x＋1)²－4（a≠0）经过点A（1，0）．

(1)、求抛物线L₁的函数表达式．

(2)、将抛物线L₁向上平移m（m＞0）个单位得到抛物线L₂ ．若抛物线L₂的顶点关于坐标原点O的对称点在抛物线L₁上，求m的值．

(3)、把抛物线L₁向右平移n（n＞0）个单位得到抛物线L₃ ，若点B（1，y₁），C（3，y₂）在抛物线L₃上，且y₁＞y₂ ，求n的取值范围．

查看试题解析

二、基础

2. 已知抛物线 $C_{1}$ 的解析式为 $y = x^{2} - 2 x + 1$ ，将抛物线 $C_{1}$ 先向右平移1个单位长度，再向下平移2个单位长度得到抛物线 $C_{2}$ ．

(1)、求抛物线 $C_{2}$ 的函数关系式；

(2)、点 $A (a ， - 3)$ 能否在抛物线 $C_{2}$ 上？请说明理由．

查看试题解析
3. 把抛物线 $C_{1}$ ： $y = x^{2} - 2 x + 4$ 先向右平移3个单位长度，再向下平移2个单位长度得到抛物线 $C_{2}$ ．

(1)、求出抛物线 $C_{2}$ 的函数关系式；

(2)、若点 $A (m ， y_{1})$ ， $B (n ， y_{2})$ 都在抛物线 $C_{2}$ 上，且 $m < n < 0$ ，比较 $y_{1}$ ， $y_{2}$ 的大小，并说明理由．

查看试题解析
4. 已知抛物线 $l ： y = a x^{2} - 2 a x + a + 3 (a < 0)$ 与y轴的交点为A，顶点为P，对称轴为直线m.

(1)、求抛物线l的顶点坐标P和对称轴.

(2)、抛物线l关于点A对称的抛物线为 $l^{'}$ ，抛物线 $l^{'}$ 的顶点为Q，对称轴为直线n，在直线m和直线n上是否分别存在点E、F，使得四边形 $P E Q F$ 为正方形？若存在，请求出a的值；若不存在，请说明理由.

查看试题解析
5. 已知抛物线 $C_{1} ： y = a x^{2} - 2 a x - 3 (a > 0)$ .

(1)、当 $a = 1$ 时，求抛物线对称轴及与x轴的交点坐标；

(2)、①无论 $a$ 为何值，抛物线 $C_{1}$ 一定经过两个定点，请直接写出两个定点的坐标；
②将抛物线 $C_{1}$ 沿这两个定点所在直线翻折，得到抛物线 $C_{2}$ ，直接写出抛物线 $C_{2}$ 的解析式并求出抛物线 $C_{1}$ 与抛物线 $C_{2}$ 两个顶点的距离；

(3)、若（2）中抛物线 $C_{2}$ 的顶点到 $x$ 轴的距离为2，求 $a$ 的值.

查看试题解析
6. 如图，在平面直角坐标系中，抛物线 $y = a x^{2} + b x - 3$ 经过点 $A (2 ， 5)$ 和 $B (- 2 ， - 3)$ ．

(1)、求抛物线表达式，并根据图象写出当 $y > 0$ 时x的取值范围；

(2)、请写出一种平移方法，使得平移后抛物线的顶点落在直线 $y = 2 x$ 上，并求平移后抛物线表达式．

查看试题解析
7. 如图，在平面直角坐标系中，二次函数y＝ax²+4x﹣3图象的顶点是A，与x轴交于B，C两点，与y轴交于点D.点B的坐标是（1，0）.

(1)、求A，C两点的坐标，并根据图象直接写出当y＞0时x的取值范围.

(2)、将图象向上平移m个单位后，二次函数图象与x轴交于E，F两点，若EF＝6，求m的值.

查看试题解析
8. 如图，将抛物线P₁：y=x²+2x+m平移后得到抛物线P₂：y=x²﹣5x+n，两抛物线与y轴分别交于点C，D．抛物线P₁ ， P₂的交点E的横坐标是1，过点E作x轴的平行线，分别交抛物线P₁ ， P₂于点A，B．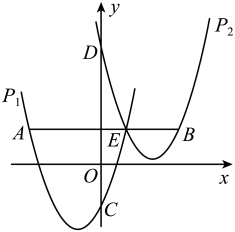

(1)、求抛物线P₁的对称轴和点A的横坐标．

(2)、求线段AB和CD的长度．

查看试题解析

三、进阶

9. 已知抛物线y=ax² +bx+ l经过点（1，-2），（-2，13）.

(1)、求a，b的值；

(2)、若（5，y₁），（n，y₂）是抛物线上不同的两点，且y₂=12-y₁ ，求n的值；

(3)、将此抛物线沿x轴平移m（m>0）个单位长度，当自变量x的值满足-1≤x≤3时，与其对应的函数值y的最小值为6，求m的值.

查看试题解析
10. 如图，抛物线C₁：y＝ax²＋2x＋c与x轴交于点A、B两点，且经过直线y=－x－3与两轴的交点A、C，其顶点为D.

(1)、求抛物线C₁的表达式及D点坐标；

(2)、将抛物线C₁向右平移，使得平移后的抛物线C₂与抛物线C₁交于点P，且∠PAB＝∠DAC，求平移后的抛物线C₂的表达式.

查看试题解析
11. 如图，在平面直角坐标系中，抛物线 $C_{1} ： y = x^{2} + b x + c$ 的图象经过 $A (- 1 ， 0)$ ， $C (0 ， - 2)$ 两点，将抛物线 $C_{1}$ 向右平移2个单位得到抛物线 $C_{2}$ ，平移后点A的对应点为点B.

(1)、求抛物线 $C_{1}$ 与 $C_{2}$ 的函数表达式；

(2)、若点M是抛物线 $C_{1}$ 上一动点，点N是抛物线 $C_{2}$ 上一动点，请问是否存在这样的点M、N，使得以A、B、M、N为顶点且以AB为边的四边形是面积为8的平行四边形？若存在，求出点M、N的坐标；若不存在，请说明理由.

查看试题解析
12. 学习完二次函数后，某班“数学兴趣小组”的同学对函数 $y = x^{2} - 2 | x | + 1$ 的图象和性质进行了探究.在经历列表、描点、连线步骤后得到其图象如图所示.请根据函数图象完成以下问题：

(1)、观察发现：
①写出该函数的一条性质；

②函数图象与x轴有个交点，所以对应的方程 $x^{2} - 2 | x | + 1 = 0$ 有个实数根；

(2)、分析思考：
③方程 $x^{2} - 2 | x | + 1 = 1$ 的解为；

④关于 $x$ 的方程 $x^{2} - 2 | x | + 1 = m$ 有4个实数根时，m的取值范围是；

(3)、延伸探究：
⑤将函数 $y = x^{2} - 2 | x | + 1$ 的图象经过怎样的平移可以得到函数 $y_{1} = {(x - 1)}^{2} - 2 | x - 1 | + 3$ 的图象，直接写出平移过程.

查看试题解析
13. 若二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象的顶点在一次函数 $y = k x + t (k \neq 0)$ 的图象上，则称 $y = a x^{2} + b x + c (a \neq 0)$ 为 $y = k x + t (k \neq 0)$ 的伴随函数，如 $y = x^{2} + 1$ 是 $y = x + 1$ 的伴随函数.

(1)、若函数 $y = x^{2} - 4$ 先向右平移2个单位，再向上平移1个单位后是 $y = - x + p$ 的伴随函数，求 $p$ 的值

(2)、若函数 $y_{1} = m x - 3 (m \neq 0)$ 的伴随函数 $y_{2} = x^{2} + 2 x + n$ 与 $x$ 轴只有一个交点，求当 $y_{1} > y_{2}$ 时， $x$ 的取值范围.

查看试题解析
14. 如图，题目中的黑色部分是被墨水污染了无法辨认的文字，导致题目缺少了一个条件而无法解答，经查询结果发现，该二次函数解析式 $y = x^{2} - 4 x + 1$ ，

已知二次函数 $y = a x^{2} + b x + c$ 的图象经过点 $A (0 ， 1)$ ， $B (1 ， - 2)$ ，．

求该二次函数的解析式．

(1)、请根据已有信息添加一个适当的条件：

(2)、当函数值 $y < 6$ ，自变量x的取值范围为：

(3)、如图1，将函数 $y = x^{2} - 4 x + 1 (x < 0)$ 的图象向右平移4个单位与 $y = x^{2} - 4 x + 1 (x \geq 4)$ 的图象组成一个新的函数图象，记为L，若点 $P (3 ， m)$ ，求m的值．

(4)、如图2，在（3）的条件下，点A的坐标为 $(2 ， 0)$ ，在L上是否存在点Q，使得 $S_{△ O A Q} = 9$ ，若存在，求出所有满足条件的点Q的坐标，不存在，说明理由．

查看试题解析
15. 如图，抛物线 $C ： y = a x^{2} + b x + c$ 的对称轴为直线 $x = - 1$ ，且抛物线经过 $M (1 ， 0) ， D (0 ， 3)$ 两点，与x轴交于点N．

(1)、点N的坐标为．

(2)、已知抛物线 $C_{1}$ 与抛物线C关于y轴对称，且抛物线 $C_{1}$ 与x轴交于点A， $B_{1}$ （点A在点 $B_{1}$ 的左边）．
①抛物线 $C_{1}$ 的解析式？

②当抛物线 $C_{1}$ 和抛物线C上y都随x的增大而增大时，请直接写出此时x的取值范围．

(3)、若抛物线 $C_{n}$ 的解析式为 $y = - (x + 1) (x - 2 - n) (n = 1 ， 2 ， 3 ⋯)$ ，抛物线 $C_{n}$ 的顶点为 $P_{n}$ ，与x轴的交点为A， $B_{n}$ （点A在，点 $B_{n}$ 的左边）．判断抛物线的顶，点 $P_{1} ， P_{2} ， P_{3} ， ⋯ ， P_{n}$ 是否在一条直线上，若在，请直接写出该直线的解析式；若不在，请说明理由．

查看试题解析

四、突破

16. 在平面直角坐标系中已知抛物线 $L_{1} ： y ＝ a x^{2} ＋ b x － 3$ 经过点 $A (- 1 ， 0)$ 和点 $B （ 3 ， 0 ）$ ，点D为抛物线的顶点.

(1)、求抛物线 $L_{1}$ 的表达式及点D的坐标；

(2)、将抛物线 $L_{1}$ 关于点 $A$ 对称后的抛物线记作 $L_{2}$ ，抛物线 $L_{2}$ 的顶点记作点E，求抛物线 $L_{2}$ 的表达式及点 $E$ 的坐标；

(3)、是否在 $x$ 轴上存在一点 $P$ ，在抛物线 $L_{2}$ 上存在一点 $Q$ ，使 $D 、 E 、 P 、 Q$ 为顶点的四边形是平行四边形？若存在，请求出 $Q$ 点坐标，若不存在，请说明理由.

查看试题解析
17. 已知抛物线 $y = a x^{2} + b x - 4 (a ， b$ 为常数， $a \neq 0)$ 交 $x$ 轴于 $A (- 1 ， 0)$ ， $B (4 ， 0)$ ，交 $y$ 轴于点 $C$ ．

(1)、求该抛物线解析式；

(2)、点 $P$ 为第四象限内抛物线上一点，连接 $P B$ ，过 $C$ 作 $C Q / / B P$ 交 $x$ 轴于点 $Q$ ，连接 $P Q$ ，求 $△ P B Q$ 面积的最大值及此时点 $P$ 的坐标；

(3)、在（2）的条件下，将抛物线 $y = a x^{2} + b x - 4$ 向右平移经过点 $(\frac{1}{2} ， 0)$ ，得到新抛物线 $y = a_{1} x^{2} + b_{1} x + c_{1}$ ，点 $E$ 是抛物线 $y = a_{1} x^{2} + b_{1} x + c_{1}$ 对称轴上的点，在坐标平面内是否存在点 $F$ ，使得以 $A$ ， $P$ ， $E$ ， $F$ 为顶点的四边形为矩形，若存在，请求出点 $F$ 的坐标；若不存在，请说明理由．

查看试题解析
18. 如图，在平面直角坐标系中，抛物线y $= - \frac{1}{2} x^{2} +$ bx+c与x轴交于A（﹣2，0）、B（4，0）两点（点A在点B的左侧），与y轴交于点C，连接AC、BC，点P为直线BC上方抛物线上一动点，连接OP交BC于点Q．

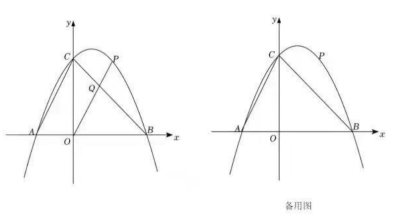(1)、求抛物线的函数表达式；

(2)、当 $\frac{P Q}{O Q}$ 的值最大时，求点P的坐标和 $\frac{P Q}{O Q}$ 的最大值；

(3)、把抛物线y $= - \frac{1}{2} x^{2} +$ bx+c沿射线AC方向平移 $\sqrt{5}$ 个单位得新抛物线y'，M是新抛物线上一点，N是新抛物线对称轴上一点，当以M、N、B、C为顶点的四边形是平行四边形时，直接写出N点的坐标．

查看试题解析
19. 定义：点P（m，m）是平面直角坐标系内一点，将函数l的图象位于直线x＝m左侧部分，以直线y＝m为对称轴翻折，得到新的函数l′的图象，我们称函数l′的函数是函数l的相关函数，函数l′的图象记作F₁ ，函数l的图象未翻折的部分记作F₂ ，图象F₁和F₂合起来记作图象F．
例如：函数l的解析式为y＝x²﹣1，当m＝1时，它的相关函数l′的解析式为y＝﹣x²+3（x＜1）．

(1)、如图，函数l的解析式为y＝﹣ $\frac{1}{2}$ x+2，当m＝﹣1时，它的相关函数l′的解析式为y＝．

(2)、函数l的解析式为y＝﹣ $\frac{3}{x}$ ，当m＝0时，图象F上某点的纵坐标为﹣2，求该点的横坐标．

(3)、已知函数l的解析式为y＝x²﹣4x+3，
①已知点A、B的坐标分别为（0，2）、（6，2），图象F与线段AB只有一个公共点时，结合函数图象，求m的取值范围；
②若点C（x，n）是图象F上任意一点，当m﹣2≤x≤5时，n的最小值始终保持不变，求m的取值范围（直接写出结果）．

查看试题解析
20. 定义：如果二次函数 $y = a_{1} x^{2} + b_{1} x + c_{1}$ ，（ $a_{1} \neq 0$ ， $a_{1}$ 、 $b_{1}$ 、 $c_{1}$ 是常数）与 $y = a_{2} x^{2} + b_{2} x + c_{2}$ $a_{2} \neq 0$ ， $a_{2}$ 、 $b_{2}$ 、 $c_{2}$ 是常数）满足 $a_{1} + a_{2} = 0$ ， $b_{1} = b_{2}$ ， $c_{1} + c_{2} = 0$ ，则这两个函致互为“旋转函数”．例如：求函数 $y = 2 x^{2} - 3 x + 1$ 的“旋转函数”，由函数 $y = 2 x^{2} - 3 x + 1$ 可知， $a_{1} = 2$ ， $b_{1} = 3$ ， $c_{1} = 1$ ．根据 $a_{1} + a_{2} = 0$ ， $b_{1} = b_{2}$ ， $c_{1} + c_{2} = 0$ 求出 $a_{2}$ 、 $b_{2}$ 、 $c_{2}$ 就能确定这个函数的“旋转函数”．
请思考并解决下面问题：

(1)、写出函数 $y = x^{2} - 4 x + 3$ 的“旋转函数”；

(2)、若函数 $y = 5 x^{2} + (m - 1) x + n$ 与 $y = - 5 x^{2} - n x - 3$ 互为“旋转函数”，求 ${(m + n)}^{2023}$ 的值；

(3)、已知函数 $y = 2 (x - 1) (x + 3)$ 的图象与x轴交于A、B两点，与y轴交于点C，点A、B、C关于原点的对称点分别是 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ ，试求证：经过点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ 的二次函数与 $y = 2 (x - 1) (x + 3)$ 互为“旋转函数”．

查看试题解析
21. 如图1，在平面直角坐标系xOy中，抛物线y＝-x²+bx+c交x轴于A，B两点（A在B左侧），交y轴于点C，且OC＝OB＝3，对称轴l交抛线于点D，交x轴于点G.

(1)、求抛物线的表达式及顶点坐标；

(2)、如图2，过点C作CH⊥DG于H，在射线HG上有一动点M（不与H重合），连接MC，将MC绕M点顺时针旋转90°得线段MN，连接DN，在点M的运动过程中， $\frac{D N}{H M}$ 是否为定值？若是，求出该定值；若不是，说明理由；

(3)、如图3，将抛物线y＝-x²+bx+c向右平移后交直线l于点E，交原抛物线于点Q且点Q在第一象限，过点Q作QP⊥x轴于点P，设点Q的横坐标为m，问：在原抛物线y＝-x²+bx+c上是否存在点F，使得以P，Q，E，F为顶点的四边形是平行四边形？若存在，求出m的值；若不存在，说明理由.

查看试题解析