备考2023年中考数学嘉兴卷变式阶梯训练：第22题

试卷更新日期：2023-04-15 类型：三轮冲刺

进入出卷网下载

一、原题

1. 某教育部门为了解本地区中小学生参加家庭劳动时间的情况，随机抽取该地区1200名中小学生进行问卷调查，并将调查问卷（部分）和结果描述如下：

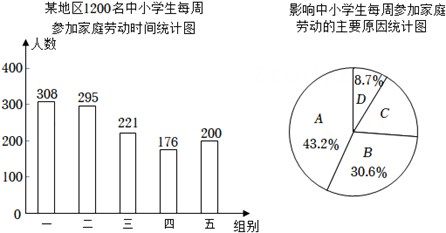
中小学生每周参加家庭劳动时间x（h）分为5组：第一组（0≤x<0.5），第二组（0.5≤x<1），第三组（1≤x<1.5），第四组（1.5≤x<2），第五组（x≥2）．

根据以上信息，解答下列问题：

(1)、本次调查中，中小学生每周参加家庭劳动时间的中位数落在哪一组？

(2)、在本次被调查的中小学生中，选择“不喜欢”的人数为多少？

(3)、该教育部门倡议本地区中小学生每周参加家庭劳动时间不少于2，请结合上述统计图，对该地区中小学生每周参加家庭劳动时间的情况作出评价，并提出两条合理化建议．

查看试题解析

二、基础

2. 为了推动阳光体育运动的广泛开展，引导学生走向操场，走进大自然，走到阳光下，积极参加体育锻炼，学校准备购买一批运动鞋供学生借用，现从各年级随机抽取了部分学生的鞋号，绘制了统计图①和图②，请根据相关信息，解答下列问题：

(1)、本次接受随机抽样调查的学生人数为，图①中m的值为；

(2)、求本次调查获取的样本数据的众数和中位数；

(3)、根据样本数据，若学校计划购买200双运动鞋，建议购买35号运动鞋多少双？

查看试题解析
3. 微信圈有篇热传的文章《如果想毁掉一个孩子，就给他一部手机!》.国际上，法国教育部宣布，小学和初中于2018年9月新学期开始，禁止学生使用手机，为了解学生手机使用情况.高新区某学校开展了“手机伴我健康行”的主题活动，学校随机抽取部分学生进行“使用手机的目的”和“每周使用手机的时间”的问卷调查，并绘制成如图①，图②的统计图.已知“查资料”的人数是40人.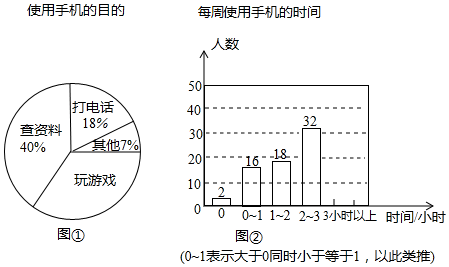

(1)、在这次调查中，一共抽取了名学生；

(2)、在扇形统计图中，“玩游戏”对应的圆心角的度数是度；

(3)、补全条形统计图；

(4)、该校共有学生2000人，请估计每周使用手机时间在2小时以上（不含2小时）的人数.

查看试题解析
4. 某校开发了“摄影、绘画、器乐、书法”四门拓展课程.为了解全校学生对每门课程的选择情况，随机抽取了部分学生进行调查（每人必选且只能选一门）.现将调查结果绘制成如下两幅不完整的统计图：
A.摄影
B.绘画
C.器乐
D.书法

(1)、本次随机调查了 ▲ 名学生；补全条形统计图中的空缺部分.

(2)、求m，n的值.

(3)、若该校共有1800名学生，请估计全校学生选择A课程的人数.

查看试题解析
5. 新冠疫情防控期间，某市某中学积极开展“停课不停学”网络教学活动.为了了解初中生每日线上学习时长t（单位：小时）的情况，在全校范围内随机抽取了部分初中生进行调查，并将所收集的数据分组整理，绘制了如图所示的不完整的条形统计图和扇形统计图.根据图中信息，解答下列问题：

(1)、在这次调查活动中，一共抽取了多少名初中生？并补全条形统计图.

(2)、若该校有2000名初中生，请你估计该校每日线上学习时长在“3≤t＜4”范围的初中生共有多少名？

查看试题解析
6. 随着社会的发展，通过微信朋友圈发布自己每天行走的步数已成为一种时尚．“健身达人”小陈为了了解好友的运动情况．随机抽取了部分好友进行调查，把6月1日那天他们行走的情况分为四个类别：A（0~5000步）（说明：“0~5000”表示大于等于0，小于等于5000，下同），B（5001~10000步），C（10001~15000步），D（15000步以上），统计结果如图所示：

请依据统计结果回答下列问题：

(1)、本次调查中，共调查了位好友；

(2)、已知A类好友人数是D类好友人数的5倍．
①请补全条形图；

②扇形图中，“A”对应扇形的圆心角为▲ 度；

③若小陈的微信朋友圈内共有150位好友，请根据调查数据，估计6月1日这天大约有多少位好友行走的步数超过10000步？

查看试题解析
7. 为了解《关于全面加强新时代大中小学劳动教育的意见》的落实情况，某校从全体学生中随机抽取部分学生，调查他们平均每周劳动时间t（单位： h），按劳动时间分为四组：A组“t <5”，B组“5≤t<7”，C组“7<t<9”，D组“t>9”.将收集的数据整理后，绘制成如下两幅不完整的统计图.
某校部分学生平均每周劳动时间条形统计图

某校部分学生平均每周劳动时间扇形统计图

根据以上信息，解答下列问题：

(1)、本次接受问卷调查的学生有多少人?并求图2中C组所在扇形圆心角的度数；

(2)、将条形统计图补充完整；

(3)、该校共有1500名学生，请你估计该校平均每周劳动时间不少于7h的学生人数.

查看试题解析
8. 某初中为增强学生亚运精神，举行了“迎亚运”书画作品创作比赛，评选小组从全校24个班中随机抽取4个班（用 A，B，C，D表示），并对征集到的作品数量进行了统计分析，得到下列两幅不完整的统计图.

(1)、评选小组采用的调查方式是普查还抽样调查？

(2)、根据上图表中的数据，补充完整作品数量条形图，并求出C班扇形的圆心角度数；

(3)、请你估计该校在此次活动中征集到的作品数量.

查看试题解析
9. 某区九年级组织了一次趣味数学竞赛，从中抽取了部分学生成绩（分数取正整数，满分为100分）进行统计，绘制统计图如图（未完整），在频数分布直方图中五组的组别从左到右依次是 $A$ 组、 $B$ 组、 $C$ 组、 $D$ 组、 $E$ 组.解答下列问题：

(1)、若 $A$ 组的频数比 $B$ 组小24，求频数分布直方图中的 $m$ ， $n$ 的值；

(2)、扇形统计图中， $D$ 部分所对的圆心角为 $a °$ ，求 $a$ 的值；

(3)、该区共有1000名初二年级学生参加趣味数学竞赛，若主办方想把一等奖的人数控制在75人，那么请你通过计算估计一等奖的分数线是在多少分以上？

查看试题解析

三、进阶

10. 某校在七、八年级举行了“食品安全知识测试”比赛，从七、八年级各随机抽取了10名学生的比赛成绩（百分制），测试成绩整理、描述和分析如下：（成绩得分用

x

表示，共分成四组：

A

．

80 \leq x < 85

，

B

．

85 \leq x < 90

，

C

．

90 \leq x < 95

，

D

．

95 \leq x < 100

）

七年级10名学生的成绩数据是：96，83，96，87，99，96，90，100，89，84．

八年级10名学生成绩数据中，在 $C$ 组中的是：94，90，92．

七，八年级抽取的学生竞赛成绩统计表

年级	平均数	中位数	众数	方差
七年级	92	93	96	34.4
八年级	92	$b$	100	50.4

八年级抽取的学生成绩扇形统计图

根据以上信息，解答下列问题：

(1)、这次比赛中哪个年级成绩更稳定，并说明理由；

(2)、求出统计图中

a

的值以及表格中

b

的值；

(3)、该校七年级共860人参加了此次比赛，估计参加此次比赛成绩优秀（

x \geq 90

）的七年级学生人数是多少？

查看试题解析

11. 某校组织了一次环保知识竞赛，九年级每班选25名同学参加比赛，成绩分为

A

，

B

，

C

，

D

四个等级，其中相应等级的得分依次记为100分、90分、80分、70分，学校将901班和902班同学的成绩进行整理并绘制成如图的统计图表.请根据信息解答下列问题：

(1)、把901班竞赛成绩统计图补充完整；

(2)、求出统计表中

a

，

b

，

c

的值；

(3)、请从以下给出的三个方面中任选一个对这次竞赛成绩的结果进行分析：

$①$ 从平均数和中位数方面来比较901班和902班的成绩；

$②$ 从平均数和众数方面来比较901班和902班的成绩；

$③$ 从 $B$ 级以上（包括 $B$ 级）的人数方面来比较901班和902班的成绩.

班级	平均数（分）	中位数（分）	众数（分）
901	$a$	$b$	90
902	87.6	80	$c$

查看试题解析

12. 农科院为了解某种小麦的长势，从中随机抽取了部分麦苗，对苗高（单位： cm）进行了测量 $.$ 根据统计的结果，绘制出如图的统计图 $①$ 和图 $②$ .
请根据相关信息，解答下列问题：

(1)、本次抽取的麦苗的株数为，图 $①$ 中 $m$ 的值为；

(2)、求统计的这组苗高数据的平均数、众数和中位数

查看试题解析

13. 针对新型冠状病毒事件，九（1）班全体学生参加学校举行的“珍惜生命，远离病毒”知识竞赛后，班长对本班成绩进行分析，制作如下的频数分布表和频数分布条形统计图

(

未完成

) .

除了60到70之间学生成绩尚未统计，还有6名学生成绩如下：90，96，98，99，99，99班长根据情况画出的扇形统计图如下：

类别	分数段	频数 $($ 人数 $)$
$A$	$60 \leq x < 70$	$a$
$B$	$70 \leq x < 80$	16
$C$	$80 \leq x < 90$	24
$D$	$90 \leq x < 100$	$b$

(1)、九（1）班有多少名学生？

(2)、求出

a

、

b

的值？并请补全条形统计图.

(3)、全校共有720名学生参加初赛，估计该校成绩

90 \leq x < 100

范围内的学生有多少人？

(4)、九（1）班甲、乙、丙三位同学的成绩并列第一，现选两人参加决赛，求恰好选中甲，乙两位同学的概率.

查看试题解析

14. 2021年下半年，乐清市进行了学生健康午休工程，促进学生健康成长.小明随机选取乐清市A，B两所学校各200名学生进行午休工程的满意度调查，满意度分值为1分、2分、3分、4分、5分五个等级，现将两所学校的满意度调查数据整理并分别绘制成统计图如图所示.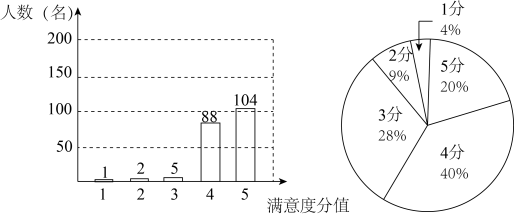

(1)、求出A，B两所学校的满意度分值的平均数、中位数、众数.

(2)、根据（1）的结果，选择适当的统计量，简略说明哪所学校的学生对健康午休工程的满意度更好.

查看试题解析

15. 某校为了解学生对“有礼衢州”城市标签的了解程度，做了一次抽样调查，调查结果共分为四个等级：A.不了解：B.基本了解：C.比较了解；D.非常了解.根据调查统计结果，绘制了如下三种不完整的统计图表.请结合统计图表，回答下列问题：

	对“有礼衢州”的了解程度	百分比
$A$	不了解	5%
$B$	基本了解	$m %$
$C$	比较了解	45%
$D$	非常了解	35%

(1)、本次参与调查的学生共有人，

m =

(2)、求扇形统计图中扇形B的圆心角度数，并补全条形统计图（要求标注人数）.

(3)、该校为提高学生对“有礼衢州”城市标签的了解程度，准备开展关于“有礼衢州”城市标签的知识竞赛，九（4）班欲从3名男生和1名女生中任选2人参加比赛，请用列表或画树状图的方法，求出恰好选中“1男1女”的概率.

查看试题解析

16. 九（1）班准备从甲、乙两名男生中选派一名参加学校组织的一分钟跳绳比赛，在相同的条件下，分别对两名男生进行了八次一分钟跳绳测试．现将测试结果绘制成如下不完整的统计图表，请根据统计图表中的信息解答下列问题：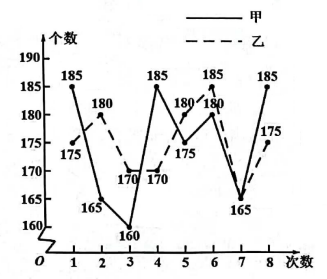

	平均数	中位数	众数
甲	175	b	c
乙	a	175	180，175，170

(1)、求a， b，c的值.

(2)、根据以上的数据分析，请你运用所学统计知识，评价甲乙两名男生一分钟跳绳成绩谁优.

查看试题解析

17. 劳动教育是学校贯彻“五育并举”的重要举措，某校倡议学生在家帮助父母做一些力所能及的家务．小杨随机抽取该校部分学生进行问卷调查，问卷调查表如图所示，并根据调查结果绘制了两幅不完整的统计图．

(1)、求小杨共调查了多少人，并补全条形统计图．

(2)、该校有1500名学生，根据抽样调查结果，请你估计该校平均每周做家务的时间不少于2小时的学生人数．

(3)、为了增强学生的劳动意识，现需要从A组的四位同学中抽调两位同学参与到社区服务，已知A组共由两位女生、两位男生组成，请利用树状图或列表等方法求出恰好抽调到一男一女的概率．

查看试题解析

18. 垫球是排球队常规训练的重要项目之一．下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩，测试规则为连续接球10个，每垫球到位1个记1分．

运动员甲测议成绩表

测试序号	1	2	3	4	5	6	7	8	9	10
成绩（分）	7	6	8	7	7	5	8	7	8	7

(1)、小明将三人的成绩整理后制作了下面的表格：

	平均数	中位数	众数	方差
甲	7	b	7	0.8
乙	7	7	d	0.4
丙	a	c	e	0.81

则表中a＝， b＝， c＝， d＝， e＝．

(2)、若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适？请作出简要分析．

查看试题解析

四、突破

19. 为落实国家对学生体质健康的基本要求，促进学生积极参加体育锻炼，提高体质健康水平，某校在开学初对九年级500名学生进行了第一次体质测试（满分50分），整理得如下不完整的统计表.之后制定体育锻炼计划，每天按计划进行锻炼，期中时再进行第二次体质测试，整理后绘制得如下不完整的扇形统计图（测试得分的分组与第一次相同）.

九年级学生第一次体质测试得分的频数分布表

组别	体质测试得分（分）	组中值	频数（人）
A	$0 \leq x \leq 10$	5	15
B	$10 < x \leq 20$	15	50
C	$20 < x \leq 30$	25	100
D	$30 < x \leq 40$	35	a
E	$40 < x \leq 50$	45	130

(1)、频数分布表中a的值为，扇形统计图中C部分所对应的圆心角的度数为；

(2)、请选择一个合适的统计量，评价该校九年级学生这半学期每天按计划进行体育锻炼的效果；

(3)、若体质测试得分达到30分以上为达标，则九年级学生第二次体质测试达标率比第一次提升了多少？

查看试题解析

20. 2月20日，北京冬奥会圆满落幕，在无与伦比的盛会背后，有着许多志愿者的辛勤付出．在志愿者招募之时，甲、乙两所大学积极开展了志愿者选拔活动，现从两所大学参加测试的志愿者中分别随机抽取了10名志愿者的测试成绩进行整理和分析（成绩得分用x表示，共分成四组：A．

60 \leq x < 70

，B．

70 \leq x < 80

，C．

80 \leq x < 90

，D．

90 \leq x < 100

），下面给出了部分信息：

甲校10名志愿者的成绩（分）为： $65 ， 92 ， 87 ， 84 ， 97 ， 87 ， 96 ， 79 ， 95 ， 88$ ．

乙校10名志愿者的成绩分布如扇形图所示，其中在C组中的数据为： $86 ， 88 ， 89$ ．

甲、乙校抽取的志愿者成绩统计表

	甲校	乙校
平均数	87	87
中位数	87.5	b
方差	$S_{甲}^{2}$	79.4
众数	c	95

(1)、由上表填空：

a =

，

b =

，

S_{甲}^{2} =

c =

；

(2)、你认为哪个学校的志愿者测试成绩的总体水平较好？请至少写出两条理由；

(3)、若甲校参加测试的志愿者有200名，请估计甲校成绩在90分及以上的约有多少人．

查看试题解析

21. 绵阳某公司销售部统计了每个销售员在某月的销售额，绘制了如下折线统计图和扇形统计图：

设销售员的月销售额为x（单位：万元）.销售部规定：当x＜16时为“不称职”，当16≤x＜20时为“基本称职”，当20≤x＜25时为“称职”，当x≥25时为“优秀”.根据以上信息，解答下列问题：

(1)、补全折线统计图和扇形统计图；

(2)、求所有“称职”和“优秀”的销售员月销售额的中位数和众数；

(3)、为了调动销售员的积极性，销售部决定制定一个月销售额奖励标准，凡月销售额达到或超过这个标准的销售员将获得奖励.如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖，月销售额奖励标准应定为多少万元（结果取整数）？并简述其理由.

查看试题解析
22. 某校举办“打造平安校园”活动，随机抽取了部分学生进行校园安全知识测试 $.$ 将这些学生的测试结果分为四个等级：A级：优秀；B级：良好；C级：及格；D级：不及格，并将测试结果绘制成如下统计图 $.$ 请你根据图中信息，解答下列问题：

(1)、本次参加校园安全知识测试的学生有多少人？

(2)、计算B级所在扇形圆心角的度数，并补全折线统计图；

(3)、若该校有学生1000名，请根据测试结果，估计该校达到及格和及格以上的学生共有多少人？

查看试题解析
23. 某校校本课程中心为了解该校学生喜欢校本课程的情况，采取抽样调查的办法，通过书法、剪纸、灯谜、足球四门课程的选报情况调查若干名学生的兴趣爱好，要求每位同学只能选择一门自己喜欢的课程，并将调查结果绘制成如下两幅不完整的统计图，请你根据图中提供的信息，解答：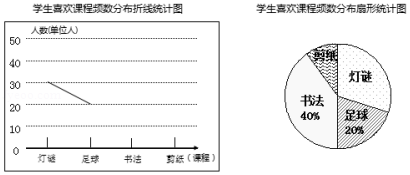

(1)、在这次调查研究中，一共调查了名学生；

(2)、喜欢剪纸的人数在扇形统计图中所占的圆心角是多少度？请补全频数分布折线统计图；

(3)、为了平衡各校本课程的人数，需要从喜欢书法课程的甲、乙、丙3人中调整2人到剪纸课程，求“甲乙两人被同时调整到剪纸课程”的概率，试用画树状图或列表说明．

查看试题解析