备考2023年中考数学嘉兴卷变式阶梯训练：第21题

试卷更新日期：2023-04-15 类型：三轮冲刺

进入出卷网下载

一、原题

1. 小华将一张纸对折后做成的纸飞机如图1，纸飞机机尾的横截面是一个轴对称图形，其示意图如图2，已知AD＝BE＝10cm，CD＝CE＝5cm，AD⊥CD，BE⊥CE，∠DCE＝40°．

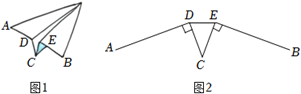(1)、连结DE，求线段DE的长．

(2)、求点A，B之间的距离．
（结果精确到0.1cm．参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）

查看试题解析

二、基础

2. 如图，为测量某建筑物BC上旗杆AB的高度，小明在距离建筑物BC底部11.4米的点F处，测得视线与水平线夹角∠AED=60°，∠BED=45°．小明的观测点与地面的距离EF为1.6米．

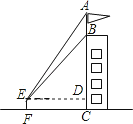(1)、求建筑物BC的高度；

(2)、求旗杆AB的高度（结果精确到0.1米）．
参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73．

查看试题解析
3. 图1是某种手机支架在水平桌面上放置的实物图，图2是其侧面的示意图，其中支杆 $A B = B C = 20 c m$ ，可绕支点C，B调节角度，DE为手机的支撑面， $D E = 18 c m$ ，支点A为DE的中点，且 $D E ⊥ A B$ ．

(1)、若支杆BC与桌面的夹角 $∠ B C M = 70 °$ ，求支点B到桌面的距离；

(2)、在（1）的条件下，若支杆BC与AB的夹角 $∠ A B C = 110 °$ ，求支撑面下端E到桌面的距离．（结果精确到1cm，参考数据： $\sin 70 ° \approx 0.94$ ， $\cos 70 ° \approx 0.34$ ， $\tan 70 ° \approx 2.78$ ， $\sin 40 ° \approx 0.64$ ， $\cos 40 ° \approx 0.77$ ， $\tan 40 ° \approx 0.84$ ）

查看试题解析
4. 如图，一个书架上放着8个完全一样的长方体档案盒，其中左边7个档案盒紧贴书架内侧竖放，右边一个档案盒自然向左斜放，档案盒的顶点 $D$ 在书架底部，顶点 $F$ 靠在书架右侧，顶点 $C$ 靠在档案盒上，若书架内侧长为 $60 cm$ ， $∠ C D E = 53 °$ ，档案盒长度 $A B = 35 cm$ ．（参考数据： $\sin 53 ° \approx 0.80$ ， $\cos 53 ° \approx 0.60$ ， $\tan 53 ° \approx 0.75$ ）

(1)、求点 $C$ 到书架底部距离 $C E$ 的长度；

(2)、求 $E D$ 长度；

(3)、求出该书架中最多能放几个这样的档案盒．

查看试题解析
5. 倡导“低碳环保”让“绿色出行”成为一种生活常态.嘉嘉买了一辆自行车作为代步工具，各部件的名称如图1所示，该自行车的车轮半径为 $30 c m$ ，图2是该自行车的车架示意图，立管 $A B = 27 c m$ ，上管 $A C = 36 c m$ ，且它们互相垂直，座管 $A E$ 可以伸缩，点 $A$ ， $B$ ， $E$ 在同一条直线上，且 $∠ A B D = 75 °$ .

(1)、求下管 $B C$ 的长；

(2)、若后下叉 $B D$ 与地面平行，座管 $A E$ 伸长到 $18 c m$ ，求座垫 $E$ 离地面的距离.
$($ 结果精确到 $1 c m$ ，参考数据 $s i n 75 ° \approx 0.97$ ， $c o s 75 ° \approx 0.26$ ， $t a n 75 ° \approx 3.73)$

查看试题解析
6. 图1是某小区入口实景图，图2是该入口抽象成的平面示意图．已知入口BC宽3.9米，门卫室外墙AB上的O点处装有一盏路灯，点O与地面BC的距离为3.3米，灯臂OM长为1.2米（灯罩长度忽略不计），∠AOM=60°．

(1)、求点M到地面的距离；

(2)、某搬家公司一辆总宽2.55米，总高3.5米的货车从该入口进入时，货车需与护栏CD保持0.65米的安全距离，此时，货车能否安全通过？若能，请通过计算说明；若不能，请说明理由，（参考数据： $\sqrt{3}$ ≈1.73，结果精确到0.01米）

查看试题解析
7. 如图1是学生常用的一种圆规，其手柄AB=8mm，两脚BC=BD=56mm，如图2所示．当∠CBD=74°时：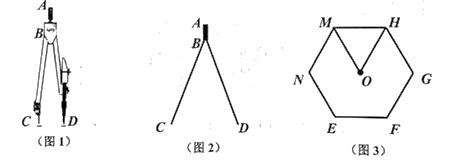

(1)、求A离纸面CD的距离．

(2)、用该圆规作如图3所示正六边形，求该正六边形的周长．
（参考数据：sin37°≈0.60，cos37°≈0.80，sin74°≈0.96，cos74°≈0.28，结果精确到0.1）

查看试题解析
8. 如图，为了测出旗杆AB的高度，在旗杆前的平地上选择一点C，测得旗杆顶部A的仰角为45°，在C，B之间选择一点D(C，D，B三点共线)，测得旗杆顶部A的仰角为75°，且CD＝8m.(参考数据： $\sqrt{2}$ ≈1.414； $\sqrt{3}$ ≈1.732； $\sqrt{5}$ ≈2.236.)

(1)、求点D到CA的距离(结果保留根号).

(2)、求旗杆AB的高(结果精确到0.01m).

查看试题解析
9. 如图是一种单人网球训练器示意图，横杆 $A B = 0.5 m$ ， $A B ⊥ A C$ ，点D表示网球的位置，横杆可绕点A旋转，通过旋转横杆，调节网球的高度，从而适应不同高度的人进行训练.现旋转AB，将点B旋转至点 $B'$ ，使 $∠ C A B' = 126 °$ .（ $s i n 36 ° \approx 0.588$ ， $c o s 36 ° \approx 0.809$ ， $t a n 36 ° \approx 0.727$ ， $π \approx 3.142$ ）

(1)、求横杆端点B的运动路径长.（结果精确到0.01m）

(2)、求网球上升的高度.（结果精确到0.01m）

查看试题解析
10. 我们知道良好的坐姿有利于青少年骨骼生长，有利于身体健康，那么首先要有正确的写字坐姿，身子上半部坐直，头部端正、目视前方，两手放在桌面上，两腿平放，胸膛挺起，理想状态下，如图1所示，将图1中的眼睛记为点A，腹记为点B，笔尖记为点D，且BD与桌沿的交点记为点C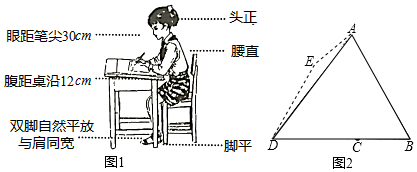
参考数据：sin53°≈0.80，cos53°≈0.60，．tan53°≈1.33， $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73）

(1)、若∠ADB＝53°，∠B＝60°，求A到BD的距离及C、D两点间的距离（结果精确到1cm）．

(2)、老师发现小红同学写字姿势不正确，眼睛倾斜至图2的点E，点E正好在CD的垂直平分线上，且∠BDE＝60°，于是要求其纠正为正确的姿势．求眼睛所在的位置应上升的距离．（结果精确到1cm）

查看试题解析
11. 据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过50km/h.如图，在一条笔直公路l的上方A处有一深测仪，AD⊥l于D，AD=32m，第一次探测到一辆轿车从B点匀速向D点行驶，测得∠ABD=28°，2秒后到达C点，测得∠ACD=45°（sin28°≈ $\frac{8}{17}$ ， cos28°≈ $\frac{15}{17}$ ， tan28°≈ $\frac{8}{15}$ ）

(1)、求CD，BD的长度.

(2)、通过计算，判断此轿车是否超速.

查看试题解析
12. 如图，雨伞不论张开还是收紧，伞柄AP始终平分同一平面内两条伞骨所成的角∠BAC.当伞收紧时，点D与点M重合，且点A，E（F），D在同一条直线上.已知伞骨的部分长度如下（单位：cm）：DE=DF=AE=AF=40.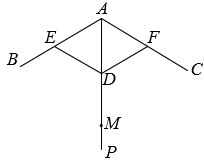

(1)、求AM的长.

(2)、当伞撑开时，量得∠BAC=110°，求AD的长.（结果精确到1cm）
参考数据： $s i n 55 ° \approx 0.8192 ， c o s 55 ° \approx 0.5736 ， t a n 55 ° \approx 1.4281$ .

查看试题解析
13. 图1是一种三角车位锁，其主体部分是由两条长度相等的钢条组成.当位于顶端的小挂锁打开时，钢条可放入底盒中（底盒固定在地面下），此时汽车可以进入车位；当车位锁上锁后，钢条按图1的方式立在地面上，以阻止底盘高度低于车位锁高度的汽车进入车位.图2是其示意图，经测量，钢条AB＝AC＝50cm，∠ABC＝47°.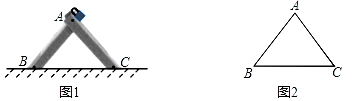

（参考数据：sin47°≈0.73，cos47°≈0.68，tan47°≈1.07）

(1)、求车位锁的底盒长BC.

(2)、若一辆汽车的底盘高度为30cm，当车位锁上锁时，问这辆汽车能否进入该车位?

查看试题解析

三、进阶

14. 已知，图①是一辆登高云梯消防车的实物图，图②是其工作示意图，起重臂 $A C$ 可伸缩（ $10 m \leq A C \leq 20 m$ ），且起重臂 $A C$ 可绕点 $A$ 在一定范围内转动，张角为 $∠ C A E$ （ $90 ° \leq ∠ C A E \leq 150 °$ ），转动点 $A$ 距离地面 $B D$ 的高度 $A E$ 为 $3.5 m$ .

(1)、当起重臂 $A C$ 长度为 $12 m$ ，张角 $∠ C A E$ 为120°时，求云梯消防车最高点 $C$ 距离地面的高度 $C F$ ；

(2)、某日，一居民家突发险情，该居民家距离地面的高度为 $20 m$ ，请问该消防车能否实施有效救援？（参考数据： $\sqrt{3} \approx 1.732$ ）

查看试题解析
15. 我市的白沙岛是众多海钓人的梦想之地.小明的爸爸周末去白沙岛钓鱼，将鱼竿AB摆成如图1所示.已知AB＝4.8m，鱼竿尾端A离岸边0.4m，即AD＝0.4m.海面与地面AD平行且相距1.2m，即DH＝1.2m.

（参考数据：sin37°＝co553° $\approx \frac{3}{5}$ ，cos37°＝sin53° $\approx \frac{4}{5}$ ，tan37° $\approx \frac{3}{4}$ ，sin22° $= \frac{3}{8}$ ，cos22° $\approx \frac{15}{16}$ ，tan22° $\approx \frac{2}{5}$ ）

(1)、如图1，在无鱼上钩时，鱼竿AB与地面AD的夹角∠BAD＝22°，海面上方的鱼线BC与海面HC成一定角度.求点B到海面HC的距离；

(2)、如图2，在有鱼上钩时，鱼竿与地面的夹角∠BAD＝53°，此时鱼线被拉直，鱼线BO＝5.46m，点O恰好位于海面.求点O到岸边DH的距离.

查看试题解析
16. 图1是一种木质投石机模型，其示意图如图2所示．已知 $A B = A C ， B D = 4 cm ， B C = 8 cm$ ，木架 $A G = 8 cm$ ．弹绳在自然状态时，点A，E，D在同一直线上，按压点F旋转至点 $F^{'}$ ，抛杆 $E F$ 绕点A旋转至 $E^{'} F^{'}$ ，弹绳 $D E$ 随之拉伸至 $D E^{'}$ '，测得 $∠ C D E^{'} = ∠ B A E^{'} = 90 °$ ．

(1)、求 $∠ A D G$ 的度数．

(2)、求 $A E^{'}$ 的长度，

(3)、求点E转至点 $E^{'}$ 的过程中，点E垂直上升的高度．

查看试题解析
17. 如图1是可调节高度和桌面角度的电脑桌，它的左视图可以抽象成如图2所示的图形，底座 $A B$ 长为 $60 cm$ ，支架 $C D$ 垂直平分 $A B$ ，桌面 $E F$ 的中点 $D$ 固定在支架 $C D$ 处， $E F$ 宽为 $60 cm$ .身高为 $160 cm$ 的使用者 $M N$ 站立处点 $M$ 与点 $A ， B$ 在同一条直线上， $M A = 20 cm$ .点 $N$ 到点 $F$ 的距离是视线距离.

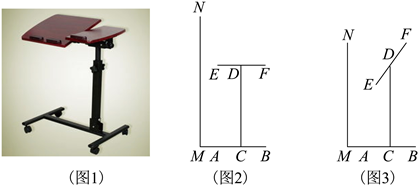(1)、如图2，当EF $∥$ AB， $C D = 100 cm$ 时，求视线距离 $N F$ 的长；

(2)、如图3，使用者坐下时，高度 $M N$ 下降 $50 cm$ ，当桌面 $E F$ 与 $C D$ 的夹角 $∠ C D E$ 为 $35^{\circ}$ 时，恰有视线NF $∥$ AB，问需要将支架 $C D$ 调整到多少 $cm$ ?（参考数据： $sin 35^{\circ} \approx 0.43 ， cos 35^{\circ} \approx 0.90 ， tan 35^{\circ} \approx 0.47$ ）

查看试题解析
18. 某课桌生产厂家研究发现，倾斜12°至24°的桌面有利于学生保持躯体自然姿势.根据这一研究，厂家决定将水平桌面做成可调节角度的桌面.新桌面的设计图如图1， AB可绕点A旋转，在点C处安装一根长度一定且C处固定，可旋转的支撑臂CD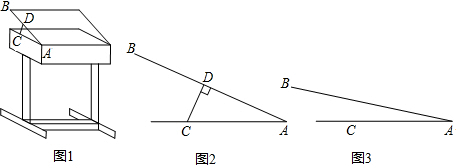， $A C = 30 cm$ .

（参考数据： $sin 24^{\circ} \approx 0.40$ ， $cos 24^{\circ} \approx 0.91$ ， $tan 24^{\circ} \approx 0.46$ ， $sin 12^{\circ} \approx 0.20$ ）

(1)、如图2，当 $∠ B A C = 24^{\circ}$ 时， $C D ⊥ A B$ ，求支撑臂 $C D$ 的长；

(2)、如图3，当 $∠ B A C = 12^{\circ}$ 时，求 $A D$ 的长.（结果保留根号）

查看试题解析
19. 图1是新冠疫情期间测温员用“额温枪”对居民张阿姨测温时的实景图，图2是其侧面示意图，其中枪柄CD和手臂BC始终在同一条直线上，枪身DE与额头F保持垂直.胳膊 $A B = 24 c m$ ， $B D = 40 c m$ ，肘关节B与枪身端点E之间的水平宽度为28cm（即BH的长度），枪身 $D E = 8 c m$ .

(1)、求 $∠ E D C$ 的度数；

(2)、测温时规定枪身端点E与额头规定范围为 $3 c m ∼ 5 c m$ .在图2中若 $∠ A B C = 75 °$ ，张阿姨与测温员之间的距离为48cm.问此时枪身端点E与张阿姨额头F的距离是否在规定范围内，并说明理由.（结果保留小数点后两位.参考数据： $\sqrt{2} \approx 1.414$ ， $\sqrt{3} \approx 1.732$ ）

查看试题解析
20. 为加强对市内道路交通安全的监督，王警官利用无人机进行检测.某高架路有一段限速每小时60千米的道路AB（如图所示），当无人机在限速道路的正上方C处时，测得限速道路的起点A的俯角是37°，无人机继续向右水平飞行220米到达D处，此时又测得起点A的俯角是30°，同时测得限速道路终点B的俯角是45°（注：即四边形ABDC是梯形）.

(1)、求限速道路AB的长（精确到1米）；

(2)、如果李师傅在道路AB上行驶的时间是1分20秒，请判断他是否超速？并说明理由.
（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75， $\sqrt{3} \approx 1.73$ ）

查看试题解析
21. 你还记得小时候的竹椅子么？一款老式竹编靠背椅的尺寸如图1（单位： $cm$ ），如图2是它的侧面示意图，坐高 $A B = 35$ ，宽 $B C = 31$ ，背长 $D E = 39$ ，总高 $E F = 71$ .

(1)、求 $\tan ∠ E D A$ 的值.

(2)、现需特制一款椅子，保持总高不变，现要求靠背的倾斜角从 $∠ E G H$ 调整为 $∠ E G^{'} H^{'} = 70 °$ ，已知 $A H = 12$ ，则将横档 $G H$ 长度保持不变直接向下调整多少厘米即可？
参考数据： $\sin 70 ° \approx 0.94$ ， $\cos 70 ° \approx 0.34$ ， $\tan 70 ° \approx 2.75$

查看试题解析

四、突破

22. 图1为科研小组研制的智能机器，水平操作台为l，底座AB固定，高AB为50cm，始终与平台l垂直，连杆BC长度为60cm，机械臂CD长度为40cm，点B，C是转动点，AB，BC与CD始终在同一平面内，张角∠ABC可在60°与120°之间（可以达到60°和120°）变化，CD可以绕点C任意转动.

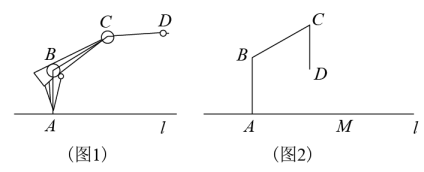(1)、转动连杆BC，机械臂CD，使张角∠ABC最大，且CD∥AB，如图2，求机械臂臂端D到操作台l的距离DE的长.

(2)、转动连杆BC，机械臂CD，要使机械臂端D能碰到操作台l上的物体M，则物体M离底座A的最远距离和最近距离分别是多少？

查看试题解析
23. 为了监控危险路段的车辆行驶情况，通常会设置电子眼进行区间测速.如图电子眼位于点P处，离地面的铅垂高度PQ为11米；离坡AB的最短距离是11.2米，坡AB的坡比为3：4；电子眼照射在A 处时，电子眼的俯角为30°，电子眼照射在坡角点B处时，电子眼的俯角为70°.（A、B、P、Q在同一平面内）

(1)、求路段BQ的长；（sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）

(2)、求路段AB的长；（ $\sqrt{3}$ ≈1.7，结果保留整数）

(3)、如图的这辆车看成矩形KLNM，车高2米，当PA过M点时开始测速，PB过M点时结束测速，若在这个测速路段车辆所用的时间是1.5秒.该路段限速5米/秒，计算说明该车是否超速？

查看试题解析
24. 测量金字塔高度：如图1，金字塔是正四棱锥 $S - A B C D$ ，点O是正方形 $A B C D$ 的中心 $S O$ 垂直于地面，是正四棱锥 $S - A B C D$ 的高，泰勒斯借助太阳光.测量金字塔影子 $△ P B C$ 的相关数据，利用平行投影测算出了金字塔的高度，受此启发，人们对甲、乙、丙三个金字塔高度也进行了测量.甲、乙、丙三个金字塔都用图1的正四棱锥 $S - A B C D$ 表示.

(1)、测量甲金字塔高度：如图2，是甲金字塔的俯视图，测得底座正方形 $A B C D$ 的边长为 $80 m$ ，金字塔甲的影子是 $△ P B C ， P C = P B = 50 m$ ，此刻，1米的标杆影长为0.7米，则甲金字塔的高度为m.

(2)、测量乙金字塔高度：如图1，乙金字塔底座正方形 $A B C D$ 边长为 $80 m$ ，金字塔乙的影子是 $△ P B C$ ， $∠ P C B = 75 ° ， P C = 40 \sqrt{2} m$ ，此刻1米的标杆影长为0.8米，请利用已测出的数据，计算乙金字塔的高度.

查看试题解析