备考2023年中考数学嘉兴卷变式阶梯训练：第20题

试卷更新日期：2023-04-15 类型：三轮冲刺

进入出卷网下载

一、原题

1. 6月13日，某港口的湖水高度y（cm）和时间x（h）的部分数据及函数图象如下：

x(h)	…	11	12	13	14	15	16	17	18	…
Y(cm	…	189	137	103	80	101	133	202	260	…

（数据来自某海洋研究所）

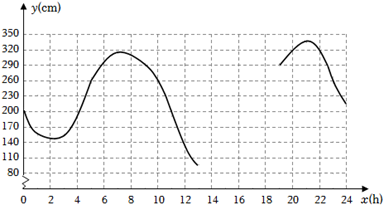(1)、数学活动：

①根据表中数据，通过描点、连线（光滑曲线）的方式补全该函数的图象．

②观察函数图象，当x＝4时，y的值为多少？当y的值最大时，x的值为多少？

(2)、数学思考：

请结合函数图象，写出该函数的两条性质或结论．

(3)、数学应用：

根据研究，当潮水高度超过260cm时，货轮能够安全进出该港口.请问当天什么时间段适合货轮进出此港口？

查看试题解析

二、基础

2. 由于惯性的作用，行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止，这段距离称为“刹车距离”．某公司设计了一款新型汽车，现在对它的刹车性能（车速不超过150 km/h）进行测试，测得数据如下表：
车速v（km/h）
0
30
60
90
120
150
刹车距离s（m）
0
7.8
19.2
34.2
52.8
75

(1)、以车速v为横坐标，刹车距离s为纵坐标，在坐标系中描出表中各组数值所对应的点，并用平滑曲线连接这些点；

(2)、由图表中的信息可知：
①该型汽车车速越大，刹车距离越（填“大”或“小”）；
②若该型汽车某次测试的刹车距离为40 m，估计该车的速度约为km/h；

(3)、若该路段实际行车的最高限速为120 km/h，要求该型汽车的安全车距要大于最高限速时刹车距离的3倍，则安全车距应超过m．

查看试题解析
3. 已知函数 $y_{1} = {\begin{array}{l} - x + 1 (0 \leq x < 1) \\ \frac{1}{x} (x \geq 1) \end{array}$

(1)、当 $x = 2$ 时， $y_{1} =$ ；

(2)、已知点 $A (m ， 1)$ 在函数图象上，则求m的值；

(3)、已知函数 $y_{2}$ 的图象与函数 $y_{1}$ 的图象关于y轴对称，我们称 $y_{2}$ 为 $y_{1}$ 的镜像函数．请在图中画出 $y_{1}$ ， $y_{2}$ 的图象．

(4)、若直线 $y_{3} = x + a$ 与函数 $y_{1}$ 和 $y_{2}$ 的图象有且只有一个交点，请直接写出a的取值范围．

查看试题解析

4. 请同学们结合探究一次函数，反比例函数，二次函数图象和性质的过程，继续探究函数

y = \frac{6}{x + 1}

的图像和性质．

第一步：列表；

x	……	-7	-5	a	-3	-2	0	1	2	3	5	……
$y = \frac{6}{x + 1}$	……	-1	-1.5	-2	-3	-6	6	3	2	b	1	……

第二步：描点；

第三步：连线．

(1)、计算表中a和b的值：a： b：，并将该函数在直线

x = - 1

左侧部分的图像描点画出；

(2)、试着描述函数

y = \frac{6}{x + 1}

的性质：

①x的取值范围：；②y的取值范围：；

③图像的增减性：；④图像的对称性：；

(3)、已知一次函数

y = k x + b

与

y = \frac{6}{x + 1}

相交于点C（1，3），D（-5，-1.5），结合图象直接写出关于x的不等式

k x + b > \frac{6}{x + 1}

的解集．

查看试题解析

5. 小云在学习二次根式以后突发奇想，就尝试着来研究和二次根式相关的函数

y = \sqrt{x^{2} + 9} - 1 .

下面是小云对其探究的过程，请补充完整：

(1)、y与x的几组对应值如表：

x	$\dots$	$- 3$	$- 2$	$- 1$	0	1	2	3	$\dots$
y	$\dots$	$3 \sqrt{2} - 1$	m	$\sqrt{10} - 1$	2	$\sqrt{10} - 1$	n	$3 \sqrt{2} - 1$	$\dots$

可得m= ，n= ．

(2)、结合表，在平面直角坐标系xOy中，画出当

x \geq 0

时的函数y的图象．

(3)、结合表格和图象，请写出函数

y = \sqrt{x^{2} + 9} - 1

的三条性质．

查看试题解析

6. 利用初中阶段我们学习函数知识的方法探究一下形如 $y = x^{3}$ 的函数：

(1)、由表达式 $y = x^{3}$ ，得出函数自变量x的取值范围是；

(2)、由表达式 $y = x^{3}$ 还可以分析出，当 $x ⩾ 0$ 时， $y ⩾ 0$ ，y随x增大而增大；当 $x < 0$ 时，y0，y随x增大而．

(3)、如图中画出了函数 $y = x^{3} (x ⩾ 0)$ 的图象，请你画出 $x < 0$ 时的图象；

(4)、根据图象，再写出 $y = x^{3}$ 的一条性质．

查看试题解析

7. 如图1，小明用一张边长为

6 dm

的正三角形硬纸板设计一个无盖的正三棱柱糖果盒，从三个角处分别剪去一个形状大小相同的四边形，其一边长记为

x dm

，再折成如图2所示的无盖糖果盒，它的容积记为

y {dm}^{3}

(1)、

y

关于

x

的函数关系式是，自变量

x

的取值范围是.

(2)、为探究

y

随

x

的变化规律，小明类比二次函数进行了如下探究：

①列表：请你补充表格中的数据：

$x$	0	0.5	1	1.5	2	2.5	3
$y$	0	3.125		3.375		0.625	0

②描点：请你把上表中各组对应值作为点的坐标，在平面直角坐标系中描出相应的点；

③连线：请你用光滑的曲线顺次连接各点.

(3)、利用函数图象解决：

①该糖果盒的最大容积是 ▲ ；

②若该糖果盒的容积超过 $2 {dm}^{3}$ ，请估计糖果盒的底边长 $a$ 的取值范围.（保留一位小数）

查看试题解析

8. 某学校STEAM社团在进行项目化学习时，根据古代的沙漏模型（图1）制作了一套“沙漏计时装置”，该装置由沙漏和精密电子秤组成，电子秤上放置盛沙容器．沙子缓慢匀速地从沙漏孔漏到精密电子称上的容器内，可以通过读取电子秤的读数计算时间（假设沙子足够）．该实验小组从函数角度进行了如下实验探究：
实验观察：实验小组通过观察，每两小时记录一次电子秤读数，得到下表．

漏沙时间x（h）

0

2

4

6

8

电子秤读数y（克）

6

18

30

42

54

(1)、探索发现：建立平面直角坐标系，如图2，横轴表示漏沙时间x，纵坐标表示精密电子称的读数y，描出以表中的数据为坐标的各点．

(2)、观察上述各点的分布规律，判断它们是否在同一条直线上，如果在同一条直线上，请你建立适当的函数模型，并求出函数表达式，如果不在同一条直线上，请说明理由．

(3)、结论应用：应用上述发现的规律估算：若漏沙时间为9小时，精密电子称的读数为多少？

(4)、若本次实验开始记录的时间是上午7：30，当精密电子秤的读数为72克时是几点钟？

查看试题解析

三、进阶

9. 小明根据学习函数的经验，对 $y = x + \frac{1}{x}$ 的图像与性质进行了研究．
下面是小明的探究过程，请补充完整：

(1)、函数 $y = x + \frac{1}{x}$ 的自变量x的取值范围．

(2)、下表列出y与x的几组对应值，请写出m、n的值，m＝， n＝．
x
…
$- 3$
$- 2$
$- 1$
$- \frac{1}{2}$
$- \frac{1}{3}$
$\frac{1}{3}$
$\frac{1}{2}$
1
2
3
4
…
y
…
$- \frac{10}{3}$
$- \frac{5}{2}$
$- 2$
$- \frac{5}{2}$
$- \frac{10}{3}$
m
$\frac{5}{2}$
2
$\frac{5}{2}$
n
$\frac{17}{4}$
…

(3)、如图，在平面直角坐标系xOy中，指出以上列表中各对对应值为坐标的点，根据描出的点，画出该函数的图象．

(4)、结合函数图象，完成：
①当 $y = - \frac{17}{4}$ 时，x＝．
②写出该函数的一条性质．
③若方程 $x + \frac{1}{x} = t$ 有两个不相等的实数根，则t的取值范围是．

查看试题解析

10. 通过“列表、描点、连线”画出函数图象，观察图象得出函数的性质是研究函数的常用方法．某兴趣小组对函数

y = \frac{6}{x - 1}

的图象和性质进行了探究，探究过程如下，请补充完整：

(1)、函数

y = \frac{6}{x - 1}

的自变量取值范围是．

(2)、列表：

$x$	…	$- 3$	$- 2$	$- 1$	0	2	3	4	5	…
$y$	…	$- \frac{3}{2}$	$- 2$	$- 3$	$- 6$	6	$m$	2	$\frac{3}{2}$	…

则表中 $m$ 的值为．

(3)、描点，连线：根据表中数据，在如图所示平面直角坐标系中描点，并画出函数图象．

(4)、观察函数图象，写出该函数的一条性质：．

(5)、直线

y = - \frac{1}{6} x + \frac{13}{6}

与函数

y = \frac{6}{x - 1}

的图象的交点个数是个．

查看试题解析

11. 探究函数性质时，我们经历了列表、描点、连线画出函数图象，观察分析图像特征，概括函数性质的过程．结合已有的学习经验，请画出函数

y_{1} = - \frac{12}{x^{2} + 2}

的图象并探究该函数的性质．

x	…	$- 4$	$- 3$	$- 2$	$- 1$	0	1	2	3	4	…
$y_{1}$	…	$- \frac{2}{3}$	a	$- 2$	$- 4$	b	$- 4$	$- 2$	$- \frac{12}{11}$	$- \frac{2}{3}$	…
$y_{2}$				c	d	e	f	g

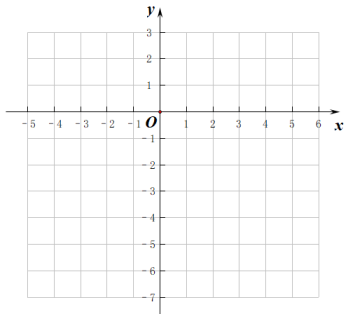(1)、列表，写出表中a，b的值：a＝ ▲ ， b＝ ▲ ；描点、连线，在所给的平面直角坐标系中画出该函数的图象．

(2)、观察函数图象，判断下列关于函数性质的结论是否正确，在下面横线上填入“序号”或填入“无”，正确的是，错误的是．

①函数 $y_{1} = - \frac{12}{x^{2} + 2}$ 的图象关于y轴对称；

②当 $x = 0$ 时，函数 $y_{1} = - \frac{12}{x^{2} + 2}$ 有最小值，最小值为 $- 6$ ；

③在自变量的取值范围内函数y的值随自变量x的增大而减小．

(3)、已知二次函数

y_{2} = x^{2} - 6

，请你写出表中c，d，e，f，g的值：c＝ ▲ ， d＝ ▲ ， e＝ ▲ ， f＝ ▲ ， g＝ ▲ ，并在所给的同一坐标系中画出函数

y_{2} = x^{2} - 6

的图像，结合你所画的函数图象，直接写出不等式

6 - \frac{12}{x^{2} + 2} < x^{2}

的解集．

查看试题解析

12. 已知点A（2，a）、B（﹣8，b）两点在函数y＝ $\frac{8}{| x |}$ 的图象上．

(1)、直接写出a＝， b＝，并在网格内画出函数y＝ $\frac{8}{| x |}$ 的图象；

(2)、将点C（6，c）绕A点逆时针旋转90°得到点D，若点D恰好落在函数图象上，求c的值；

(3)、设AB的解析式为y＝kx+m，请直接写出不等式kx+m＞ $\frac{8}{| x |}$ 的解集．

查看试题解析

13. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后，进一步研究了函数

y = \frac{2}{| x |}

的图象与性质，其探究过程如下：

(1)、绘制函数图象，

列表：下表是x与y的几组对应值，其中m＝．

x	…	﹣3	﹣2	﹣1	$- \frac{1}{2}$	$\frac{1}{2}$	1	2	3	…
y	…	$\frac{2}{3}$	1	2	4	4	2	1	m	…

描点：根据表中各组对应值（x，y），在平面直角坐标系中描出各点，请你描出剩下的点；

连线：用平滑的曲线顺次连接各点，已经画出了部分图象，请你把图象补充完整；

(2)、通过观察图象，下列关于该函数的性质表述正确的是：；（填写代号）

①函数值y随x的增大而增大；② $y = \frac{2}{| x |}$ 关于y轴对称；③ $y = \frac{2}{| x |}$ 关于原点对称；

(3)、在上图中，若直线y＝2交函数

y = \frac{2}{| x |}

的图象于A，B两点（A在B左边），连接OA．过点B作BC

∥

OA交x轴于C．则

S_{四 边 形 O A B C}

＝．

查看试题解析

14. 学习函数时，我们经历了“确定函数解析式、画出函数图象、利用函数图象研究函数性质、利用函数性质解决问题”的学习过程．以下是我们研究函数 $y = - | x | + 2$ 的图象和性质的部分过程，请按要求完成下列问题．

(1)、列表：y与x的部分对应值如下表，则 $m =$ ， $n =$ ；
x
…
-3
-2
-1
0
1
2
3
…
y
…
m
0
1
2
1
n
$- 1$
…

(2)、描点、连线：根据上表中的数据，在平面直角坐标系中画出函数 $y = - | x | + 2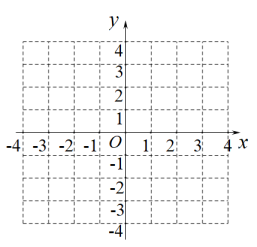$ 的图象；

(3)、结合图象，写一条函数 $y = - | x | + 2$ 的性质：；

(4)、根据函数图象填空：
①方程 $- | x | + 2 = 2$ 有个解；
②若关于x的方程 $- | x | + 2 = a$ 无解，则a的取值范围是．

查看试题解析
15. 在初中阶段的函数学习中，我们经历了列表，描点，连线画函数图象，并结合图象研究函数性质的过程．若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数．下面我们参照函数学习的过程与方法，探究分段函数 $y = {\begin{cases} - \frac{2}{x} ， x \leq - 2 \\ | x + 1 | ， x > - 2 \end{cases}$ 的图象与性质，探究过程如下，请补充完整，

(1)、列表：
x
…
－6
－5
－4
－3
－2
－1
0
1
2
3
…
y
…
$\frac{1}{3}$
$\frac{2}{5}$
m
$\frac{2}{3}$
1
n
1
2
3
4
…
其中， $m =$ ， $n =$ ．

(2)、描点：在平面直角坐标系中，以自变量x的取值为横坐标，以相应的函数值y为纵坐标，描出相应的点，如图所示，请画出函数的图象．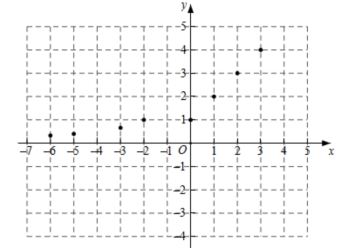

(3)、研究函数并结合图象与表格，回答下列问题：
①点 $A (- 3 ， y_{1})$ ， $B (- \frac{3}{4} ， y_{2})$ ， $C (x_{1} ， \frac{1}{2})$ ， $D (x_{2} ， \frac{5}{4})$ 在函数图象上，则 $y_{1}$ ▲ $y_{2}$ ， $x_{1}$ ▲ $x_{2}$ ；（填“＞”，“＝”或“＜”）；
②直线 $y = t$ 与图象相交，交点依次从左到右为M，N，K三点，如果 $M N = N K$ ，求t的值．

查看试题解析

16. 有这样一个问题：探究函数

y = \frac{3}{| x - 1 |}

的图象与性质，并解决问题：小聪根据学习函数的经验，对问题进行了探究.下面是小聪的探究过程，请补充完整：

(1)、函数

y = \frac{3}{| x - 1 |}

的自变量x的取值范围是；

(2)、取几组y与x的对应值，填写在下表中，其中m的值为；

x	…	－2	－1	$- \frac{1}{2}$	0	$\frac{1}{2}$	$\frac{3}{2}$	$\frac{5}{2}$	3	4	…
y	…	1	$\frac{3}{2}$	2	3	6	6	m	$\frac{3}{2}$	1	…

(3)、如下图，根据（2）中表里各组对应值（x，y），在平面直角坐标系中描出了各点，画出了部分图象，请你把图象补充完整；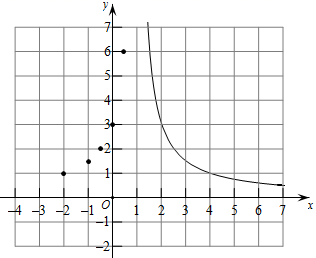

(4)、获得性质，解决问题：

①通过观察、分析、证明，可知函数 $y = \frac{3}{| x - 1 |}$ 的图象是轴对称图形，它的对称轴是；

②若点M（ $x_{1}$ ， $y_{1}$ ）、N（ $x_{2}$ ， $y_{2}$ ）在函数 $y = \frac{3}{| x - 1 |}$ 的图象上，且1＜ $x_{2}$ ＜ $x_{1}$ ，则 $y_{1}$ $y_{2}$ （填 “ ＜ ”或 “ ＞ ”）.

查看试题解析

17. 探究函数性质时，我们经历了列表、描点、连线画出函数图象，观察分析图象特征，概括函数性质的过程，以下是我们研究函数y＝|

\frac{2 x}{x - 2}

|的性质及其应用的部分过程，请按要求完成下列各小题：

(1)、请直接写出表中m，n的值，并在图中补全该函数图象；

⋯

﹣5

﹣4

﹣3

﹣2

﹣1

$\frac{3}{2}$

⋯

y＝| $\frac{2 x}{x - 2}$ |

⋯

$\frac{10}{7}$

$\frac{4}{3}$

$\frac{6}{5}$

$\frac{2}{3}$

$\frac{10}{3}$

$\frac{14}{5}$

⋯

(2)、结合函数图象，直接写出该函数的一条性质；

(3)、已知函数y＝

\frac{4}{5} x + \frac{18}{5}

的图象如图所示，结合你所画的函数图象，直接写出不等式

\frac{4}{5} x + \frac{18}{5} ⩾ | \frac{2 x}{x - 2} |

的解集（保留1位小数，误差不超过0.2）.

查看试题解析

18. 在并联电路中，电源电压为

U_{总} = 6 V

，小亮根据“并联电路分流不分压”的原理知道：

I_{总} = I_{1} + I_{2}

（

I_{1} = \frac{6}{R_{1}}

，

I_{2} = \frac{6}{R}

）．已知R₁为定值电阻，当R变化时，干路电流

I_{总}

也会发生变化，且干路电流

I_{总}

与R之间满足如下关系：

I_{总} = 1 + \frac{6}{R}

．

(1)、定值电阻

R_{1}

的阻值为

Ω

；

(2)、小亮根据学习函数的经验，参照研究函数的过程与方法，对比反比例函数

I_{2} = \frac{6}{R}

来探究函数

I_{总} = 1 + \frac{6}{R}

的图象与性质．

①列表：下表列出 $I_{总}$ 点与R的几组对应值，请写出m，n的值： $m =$ ， $n =$ ；

R	…	3	4	5	6	…
$I_{2} = \frac{6}{R}$	…	2	1.5	1.2	1	…
$I_{总} = 1 + \frac{6}{R}$	…	3	m	2.2	n	…

②描点、连线：在平面直角坐标系中，以①给出的R的取值为横坐标，以 $I_{总}$ 相对应的值为纵坐标，描出相应的点，并将各点用光滑曲线顺次连接起来；

(3)、观察图象并分析表格，回答下列问题：

① $I_{总}$ 随R的增大而；（填“增大”或“减小”）

②函数 $I_{总} = 1 + \frac{6}{R}$ 的图象是由 $I_{2} = \frac{6}{R}$ 的图象向平移个单位而得到．

查看试题解析

四、突破

19. 请阅读下列解题过程：解一元二次不等式：x²-2x-3＜0．

解：设x²-2x-3＝0，解得：x₁＝-1，x₂＝3，

则抛物线y＝x²-2x-3与x轴的交点坐标为（-1，0）和（3，0）．

画出二次函数y＝x²-2x-3的大致图象（如图所示）．

由图象可知：当-1＜x＜3时函数图象位于x轴下方，此时y＜0，即x²-2x-3＜0．

所以一元二次不等式x²-2x-3＜0的解集为：-1＜x＜3．

通过对上述解题过程的学习，按其解题的思路和方法解答下列问题：

(1)、上述解题过程中，渗透了下列数学思想中的和 .（只填序号）

①转化思想；②分类讨论思想；③数形结合思想．

(2)、用类似的方法解一元二次不等式：-x²+2x＞0．

(3)、某“数学兴趣小组”根据以上的经验，对函数y＝-（x-1）（|x|-3）的图象和性质进行了探究，探究过程如下，请补充完整：

①自变量x的取值范围是▲；x与y的几组对应值如表，其中m＝▲ ．

x	…	-4	-3	-2	-1	0	1	2	3	4	…
y	…	5	0	-3	m	-3	0	1	0	-3	…

②如图，在直角坐标系中画出了函数y＝-（x-1）（|x|-3）的部分图象，用描点法将这个图象补画完整．

③结合函数图象，解决下列问题：

解不等式：-3≤-（x-1）（|x|-3）≤0．

查看试题解析

20. 甲、乙两人在相邻的直跑道上进行了一次 $60 m$ 折返跑（即跑 $60 m$ 后马上折返跑回起点）训练．甲完成一次折返跑用时 $20 s$ ，乙完成一次折返跑用时 $24 s$ ．假设两人同时从同一起跑线出发，且跑步过程中保持匀速．设甲、乙两人离起点的距离为 $y (m)$ ，跑步时间为 $x (s)$ ．

(1)、请在下面的直角坐标系中分别画出在本次折返跑过程中表示两人离起点的距离y与跑步时间x之间关系的图象；

(2)、分别写出甲折返后和乙折返前y与x之间的关系式；

(3)、在出发多少s后，两人到起点的距离相等？

(4)、当x为何值时，两人之间相距5米？（直接写出x的值即可）

查看试题解析
21. 探究通过维修路段的最短时长．
素材1：如图1，某路段(A-B-C-D 段)需要维修，临时变成双向交替通行，故在A，D处各设置红绿灯指导交通(仅设置红灯与绿灯)．

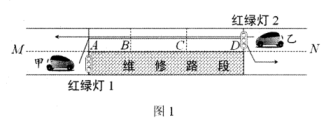
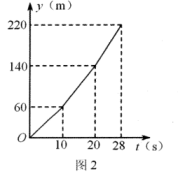
素材2：甲车先由A→D通行，乙车再由D→A通行，甲车经过AB，BC，CD段的时间分别为10s，10s，8s，它的路程y (m)与时间t(s)的关系如图2所示；两车经过BC段的速度相等，乙车经过AB段的速度是10m/s．

素材3：红绿灯1，2每114秒一个循环，每个循环内红灯、绿灯的时长如图3，且每次双向红灯时，已经进入AD段的车辆都能及时通过该路段．

[任务1]求A-B-C-D段的总路程和甲车经过BC段的速度．

[任务2]在图4中补全乙车通过维修路段时行驶的路程y(m)与时间t(s)之间的函数图象．

[任务3]丙车沿NM方向行驶，经DA段的车速与乙车经过时的速度相同，在DN段等红灯的车辆开始行驶后速度为8m/s，等红灯时车流长度每秒增加2m，问丙车在DN段从开始等待至离开点A至少需要几秒钟？

查看试题解析
22. 学习完二次函数后，某班“数学兴趣小组”的同学对函数y＝x²﹣2|x|+1的图象和性质进行了探究．在经历列表、描点、连线步骤后得到其图象如图所示．请根据函数图象完成以下问题：

(1)、观察发现：
①写出该函数的一条性质；

②函数图象与x轴有个交点，所以对应的方程x²﹣2|x|+1＝0有个实数根；

(2)、分析思考：
③方程x²﹣2|x|+1＝1的解为；

④关于x的方程x²﹣2|x|+1＝n有4个实数根时，n的取值范围是；

(3)、延伸探究：
⑤将函数y＝x²﹣2|x|+1的图象经过怎样的平移可以得到函数y＝（x+2）²﹣2|x+2|﹣3的图象，直接写出平移过程．

查看试题解析
23. 九年级某数学兴趣小组在学习了反比例函数的图象与性质后，进一步研究了函数 $y = \frac{2}{| x |}$ 的图象与性质，其探究过程如下：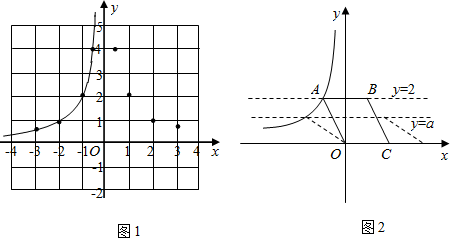

(1)、绘制函数图象，如图1．
列表：下表是 $x$ 与 $y$ 的几组对应值，其中 $m =$ ；
$x$
$\dots$
$- 3$
$- 2$
$- 1$
$- \frac{1}{2}$
$\frac{1}{2}$
1
2
3
$\dots$
$y$
$\dots$
$\frac{2}{3}$
1
2
4
4
2
$m$
$\frac{2}{3}$
$\dots$
描点：根据表中各组对应值 $(x ， y)$ ，在平面直角坐标系中描出了各点；
连线：用平滑的曲线顺次连接各点，画出了部分图象．请你把图象补充完整；

(2)、通过观察图1，写出该函数的两条性质；
①；
②；

(3)、①观察发现：如图2．若直线 $y = 2$ 交函数 $y = \frac{2}{| x |}$ 的图象于A，B两点，连接 $O A$ ，过点 $B$ 作 $B C ∥ O A$ 交 $x$ 轴于 $C$ ．则S_四_边_形OABC=；
②探究思考：将①中“直线 $y = 2$ ”改为“直线 $y = a (a > 0)$ ”，其他条件不变，则S_四_边_形OABC=；
③类比猜想：若直线 $y = a (a > 0)$ 交函数 $y = \frac{k}{| x |} (k > 0)$ 的图象于A，B两点，连接 $O A$ ，过点 $B$ 作 $B C ∥ O A$ 交 $x$ 轴于 $C$ ，则 $S_{四边形 O A B C} =$ ．

查看试题解析

车速v（km/h）	0	30	60	90	120	150
刹车距离s（m）	0	7.8	19.2	34.2	52.8	75

漏沙时间x（h）	0	2	4	6	8
电子秤读数y（克）	6	18	30	42	54