备考2023年中考数学嘉兴卷变式阶梯训练:第16题
试卷更新日期:2023-04-15 类型:三轮冲刺
一、原题
-
1. 如图,在扇形AOB中,点C,D在 上,将 沿弦CD折叠后恰好与OA,OB相切于点E,F. 已知∠AOB=120°,OA=6,则 的度数为 , 折痕CD的长为 .
二、基础
-
2. 如图,是圆O的弦, , 垂足为点C,将劣弧沿弦折叠交于的中点D,若 , 则圆O的半径为 .
 3. 如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心 , 则折痕的长为 .
3. 如图,将半径为2的圆形纸片折叠后,圆弧恰好经过圆心 , 则折痕的长为 .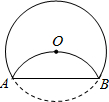 4. 如图,以AB为直径的半圆沿弦BC折叠后,AB与 相交于点D.若 ,则∠B=°
4. 如图,以AB为直径的半圆沿弦BC折叠后,AB与 相交于点D.若 ,则∠B=°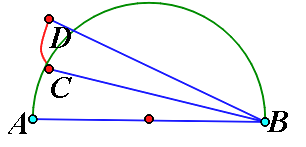 5. 如图,将弧AC沿弦AC折叠交直径AB于圆心O,则弧AC的度数是.
5. 如图,将弧AC沿弦AC折叠交直径AB于圆心O,则弧AC的度数是. 6. 如图,一个扇形纸片的圆心角为90°,半径为6,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,则阴影部分的面积为.
6. 如图,一个扇形纸片的圆心角为90°,半径为6,将这张扇形纸片折叠,使点A与点O恰好重合,折痕为CD,则阴影部分的面积为. 7. 如图,已知点 是半圆 上一点,将弧 沿弦 折叠后恰好经过点 若半圆 的半径是 则图中阴影部分的面积是.
7. 如图,已知点 是半圆 上一点,将弧 沿弦 折叠后恰好经过点 若半圆 的半径是 则图中阴影部分的面积是.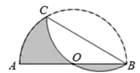 8. 如图,△ABC内接于圆,点D是AC上一点,将∠A沿BD翻折,点A正好落在圆上点E处.若∠C=50°,则∠ABE的度数为.
8. 如图,△ABC内接于圆,点D是AC上一点,将∠A沿BD翻折,点A正好落在圆上点E处.若∠C=50°,则∠ABE的度数为. 9. 如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧 上一点,则∠APB的度数为 .
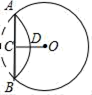
9. 如图,将⊙O沿弦AB折叠,圆弧恰好经过圆心O,点P是优弧 上一点,则∠APB的度数为 .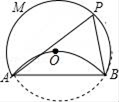 10. 如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为度.
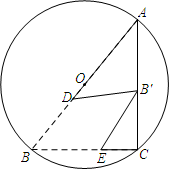
10. 如图,在⊙O中,AB为直径,点C为圆上一点,将劣弧沿弦AC翻折交AB于点D,连结CD.若点D与圆心O不重合,∠BAC=25°,则∠DCA的度数为度. 11. 如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是.
11. 如图,在矩形ABCD中,AB=4,AD=6,E是AB边的中点,F是线段BC边上的动点,将△EBF沿EF所在直线折叠得到△EB′F,连接B′D,则B′D的最小值是.
三、进阶
-
12. 如图,⊙O中,弦AC= , 沿AC折叠劣弧交直径AB于D,DB= , 则直径AB= .
 13. 如图,AC是半圆O的一条弦,将弧AC以弦AC为折线折叠后过圆心O,图中阴影部分的面积为 ,则⊙O的半径为 .
13. 如图,AC是半圆O的一条弦,将弧AC以弦AC为折线折叠后过圆心O,图中阴影部分的面积为 ,则⊙O的半径为 .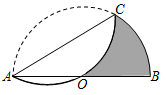 14. 如图,AC是半圆O的一条弦,以弦AC为折线将弧AC折叠后过圆心O,⊙O的半径为2,则圆中阴影部分的面积为.
14. 如图,AC是半圆O的一条弦,以弦AC为折线将弧AC折叠后过圆心O,⊙O的半径为2,则圆中阴影部分的面积为. 15. 如图,将⊙O沿弦AB折叠,恰经过圆心O,若AB=2 , 则阴影部分的面积为 .
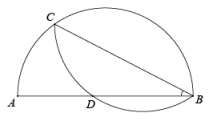
15. 如图,将⊙O沿弦AB折叠,恰经过圆心O,若AB=2 , 则阴影部分的面积为 .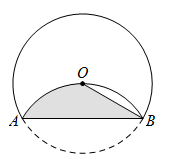 16. 如图,在R△ABC中,∠CAB=90°,D是BC边上一点,连结AD,作△ABD的外接圆,将△ADC沿直线AD翻折,若点C的对应点E落在弧BD的中点,CD= ,则BD的长为.
16. 如图,在R△ABC中,∠CAB=90°,D是BC边上一点,连结AD,作△ABD的外接圆,将△ADC沿直线AD翻折,若点C的对应点E落在弧BD的中点,CD= ,则BD的长为.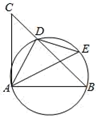 17. 如图,半圆O的半径为2,E是半圆上的一点,将E点对折到直径AB上(EE′⊥AB),当被折的圆弧与直径AB至少有一个交点时,则折痕CD的长度取值范围是.
17. 如图,半圆O的半径为2,E是半圆上的一点,将E点对折到直径AB上(EE′⊥AB),当被折的圆弧与直径AB至少有一个交点时,则折痕CD的长度取值范围是. 18. 如图,一张扇形纸片OAB中,半径OA为2,点C是 的中点,现将这张扇形纸片沿着弦AB折叠,点C恰好与圆心O重合,则图中阴影部分的面积为.
18. 如图,一张扇形纸片OAB中,半径OA为2,点C是 的中点,现将这张扇形纸片沿着弦AB折叠,点C恰好与圆心O重合,则图中阴影部分的面积为. 19. AB是半圆O的直径,AB=8,点C为半圈上的一点将此半圆沿BC所在的直线折叠, 若配给好过圆心O,则图中阴影部分的面积是 .
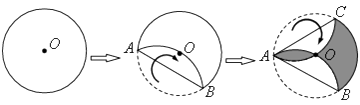
19. AB是半圆O的直径,AB=8,点C为半圈上的一点将此半圆沿BC所在的直线折叠, 若配给好过圆心O,则图中阴影部分的面积是 . 20. 如图,点 是圆形纸片的圆心,将这个圆形纸片按下列要求折叠,使弧 和弧 都经过圆心 ,已知 的半径为 ,则阴影部分的面积是.
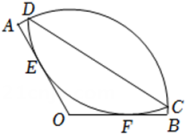
20. 如图,点 是圆形纸片的圆心,将这个圆形纸片按下列要求折叠,使弧 和弧 都经过圆心 ,已知 的半径为 ,则阴影部分的面积是.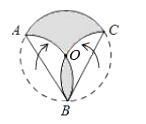 21. 如图,O是正方形ABCD边上一点,以O为圆心,OB为半径画圆与AD交于点E,过点E作⊙O的切线交CD于F,将△DEF沿EF对折,点D的对称点D'恰好落在⊙O上.若AB=6,则OB的长为.
21. 如图,O是正方形ABCD边上一点,以O为圆心,OB为半径画圆与AD交于点E,过点E作⊙O的切线交CD于F,将△DEF沿EF对折,点D的对称点D'恰好落在⊙O上.若AB=6,则OB的长为.
四、突破
-
22. 如图,是半圆的直径,是半圆的弦,沿弦折叠交直径于点.(1)当时,则的长为;(2)当 , 时,则的长为.
-