备考2023年中考数学嘉兴卷变式阶梯训练：第13题
试卷更新日期：2023-04-15 类型：三轮冲刺
一、原题
-
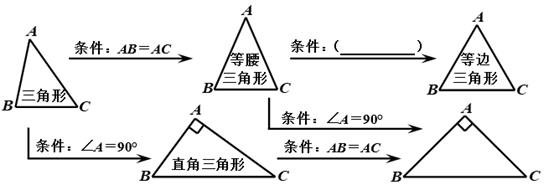
1. 小曹同学复习时将几种三角形的关系整理如图，请帮他在括号内填上一个适当的条件 ．
二、基础
-
2. 有一角为60°的等腰三角形是 ．3. 等腰三角形的一个角是60°，其中一边的长为a，这个三角形的周长为 ．4. 在△ABC中，AB＝AC，∠B＝60°，则△ABC是三角形.5. 在矩形ABCD中，对角线AC、BD相交于点O，∠AOB＝60°，AC＝6cm，则AB的长是 ．6. 矩形两条对角线的夹角为60°，对角线长为14，则该矩形较短边的边长为.7. 三角形的三边a，b，c满足+(b-c)2＝0；则三角形是三角形.8. 如图，AB＝AC＝8cm，DB＝DC，若∠ABC＝60°，则BE＝cm.
9. 如图，在△ABC中，AB＝4，BC＝6，∠B＝60°，将△ABC沿射线BC方向平移2个单位后得到△DEF，连接DC，则DC的长为.
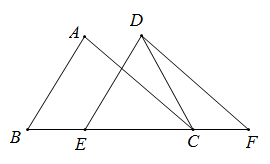10. 一块直角三角板的30°角的顶点A落在⊙O上，两边分别交⊙O于B、C两点，若弦 ，则⊙O的半径为.
三、进阶
-
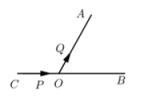
11. 已知a，b，c是△ABC的三边长，若满足|a－b|＋|b－c|＝0，△ABC的形状为12. 如图， ， 点C是BO延长线时的一点， ， 动点从点出发沿射线以的速度移动，动点Q从点O出发沿射线以的速度移动，如果点、Q同时出发，用t（s）表示移动的时间，当时，△POQ是等边三角形．
13. 如图，在△ABC中，∠C＝90°，∠B＝15°，AB的垂直平分线交BC于D，交AB于E，若DB＝10cm，则AC＝cm.
14. 如图，在等边三角形ABC中， 的平分线与 的平分线相交于D，过点D作 交AB于E，交AC于F， ，则BC的长为.
15. 如图，O是矩形ABCD对角线的交点，DE平分∠ADC交BC于点E，若∠BDE=15°，则∠COE=度
16. 如图，在四边形ABCD中，AB⊥BC，AD∥BC，∠BCD=120°，BC=2，AD=DC．P为四边形ABCD边上的任意一点，当∠BPC=30°时，CP的长为 ．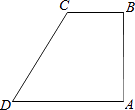
17. 如图，O是等边三角形ABC内一点，∠AOB＝110°，∠BOC＝m°，D是△ABC外一点，且△ADC≌△BOC，连接OD.当m为时，△AOD是等腰三角形.
18. 如图，在中， ， ， 是内两点，平分 ， ， 若 ， ， 则的长度.
19. 在等腰三角形ABC中， ， ，E为BC上一点， ， ，交BC于点E，点F为直线DE上一点，则 的最小值为.
20. 如图，在△ABC中，∠ABC＝60°，∠BAC＝75°，AD，CF分别是BC、AB边上的高且相交于点P，∠ABC的平分线BE分别交AD、CF于M、N.以下四个结论：①△PMN等边三角形；②除了△PMN外，还有4个等腰三角形；③△ABD≌△CPD；④当DM＝2时，则DC＝6.其中正确的结论是：（填序号）.
21. 如图， ， ， AD是∠BAC内的一条射线，且 ， P为AD上一动点，则的最大值是 ．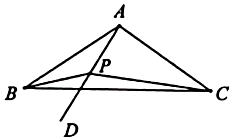
四、突破
-
22. 在△ABC中，∠A=60°，点P和点Q分别是边AC和BC上的两个动点，分别连结BP和PQ，把△ABC分割成三个三角形，若分割成的这三个三角形都是等腰三角形，则∠ABC的度数可以是.
-
