备考2023年中考数学嘉兴卷变式阶梯训练：第12题

试卷更新日期：2023-04-15 类型：三轮冲刺

进入出卷网下载

一、原题

1. 不透明的袋子中装有5个球，其中有3个红球和2个黑球，它们除颜色外都相同.从袋子中随机取出1个球，则它是黑球的概率是．

查看试题解析

二、基础

2. 一个不透明袋子中装有除颜色外其余都相同的8个球，其中白球5个，黑球3个，从中任意摸出1个球恰好为白球的概率是．

查看试题解析
3. 一个质地均匀的小正方体，6个面分别标有数字1，2，3，4，5，6．若随机投掷一次小正方体，则朝上一面的数字是3的概率是．

查看试题解析
4. 任意抛掷一枚均匀的骰子一次，朝上面的点数为4概率等于.

查看试题解析
5. 在单词“maths”中任意选择一个字母，选到字母“a”的概率是。

查看试题解析
6. 在-1，0， $\frac{7}{22}$ ， $\sqrt{2}$ ， π，0.10110中任取一个数，取到无理数的概率是．

查看试题解析
7. 已知每1000个盲盒中常规款有980个， “小隐藏” 15个， “大隐藏” 5个. 现随机抽取1盒，抽取到的是“大隐藏”的概率为.

查看试题解析
8. 有7张纸签，分别标有数字1，1，2，2，3，4，5，从中随机地抽出一张．抽出标有数字1的纸签的概率是．

查看试题解析
9. 工厂质检人员抽测某产品质量时，从同一批次共1000件产品中随机抽取100件进行检测，检测出次品1件，由此估计这一批产品中的次品件数是．

查看试题解析
10. 如图，转盘中6个扇形的面积都相等.任意转动转盘1次，当转盘停止转动时（指向两个扇形交线处时，重新转动转盘），事件“指针落在蓝色扇形中”的概率为.

查看试题解析
11. 一个小球在如图所示的地板上自由滚动，并随机停留在某块方砖上，每块方砖的大小、质地完全相同，那么该小球停留在白色区域的概率是。

查看试题解析

三、进阶

12. 在不透明的口袋中装有2个红球，1个白球，它们除颜色外无其他差别，从口袋中随机摸出一个球后，放回并摇匀，再随机摸出一个球，两次摸出的球都是红球的概率为．

查看试题解析
13. 甲袋中装有红、白两球，乙袋中装有两个红球和一个白球，两袋的球除颜色不同外其他都相同，如果分别从两个袋中各摸一球，则从两个袋中摸出的球都是白球的概率是.

查看试题解析
14. 小观在数学节中参与知识抢答活动，现有几何题6个，概率题5个，代数题9个，她从中随机抽取1个，抽中代数或几何题的概率是.

查看试题解析
15. 有三张完全一样正面分别写有字母A，B，C的卡片．将其背面朝上并洗匀，从中随机抽取一张，记下卡片上的字母后放回洗匀，再从中随机抽取一张，则抽取的两张卡片上的字母相同的概率是。

查看试题解析
16. 为了缓解中考备考压力，增加学习兴趣，李老师带领同学们玩转盘游戏.如图为两个转盘，转盘一被四等分，分别写有汉字“中”“考”“必”“胜”；转盘二被三等分，分别写有汉字“我”“必”“胜”.将两个转盘各转动一次（当指针指向区域分界线时，不记，重转），若得到“必”“胜”两字，则获得游戏一等奖，请求出获得游戏一等奖的概率为.

查看试题解析
17. 我市倡导垃圾分类投放，将日常垃圾分成四类，分别投放四种不同颜色的垃圾桶中，在“垃圾分类”模拟活动中，某同学把两个不同类的垃圾随意放入两个不同颜色的垃圾筒中，则这个同学正确分类投放垃圾的概率是.

查看试题解析
18. 现有四张正面分别标有数字－1，0，－2，3的不透明卡片，它们除数字外其余完全相同，将它们背面朝上洗均匀，随机抽取一张记作m不放回，再从余下的卡片中取一张记作n．则点P（m，n）在第二象限的概率为概率是．

查看试题解析
19. $n = 1 ， 2 ， 3 ， \cdot \cdot \cdot ， 100$ ，求和 $n + (n + 1) + (n + 2)$ 时产生进位现象的 $n$ 叫做进位数，如 $n = 3 ， 14 ， 52$ 都是进位数，在这100数中随机取一个数，不是进位数的概率是．

查看试题解析
20. 从长为3，4，5，7的四根木条中任取三根，能组成三角形的概率为．

查看试题解析
21. 从 $\frac{1}{2}$ ， $- 1$ ，1，2中任取一个数作为a的值，使抛物线 $y = a x^{2} + b x + c$ （a，b，c是常数）的开口向上的概率为.

查看试题解析

四、突破

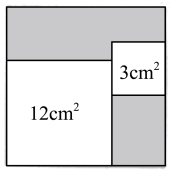
22. 在平面直角坐标系中，作△OAB，其中三个顶点分别是O(0，0)，B(1，1)，A(x，y)(－2≤x≤2，－2≤y≤2，x，y均为整数)，则所作△OAB为直角三角形的概率是．

查看试题解析
23. 如图，从一个大正方形中截去面积为 $3 c m^{2}$ 和 $12 c m^{2}$ 的两个小正方形，若随机向大正方形内投一粒米，则米粒落在图中阴影部分的概率为.

查看试题解析
24. 巧板是我国古代劳动人民的一项发明，被誉为“东方魔板”，它由五块等腰直角三角形、一块正方形和一块平行四边形组成.如图是利用七巧板拼成的正方形，随机向该图形内抛一枚小针，则针尖落在阴影部分的概率为 .

查看试题解析
25. 如图，已知 $⊙ O$ 的两条直径 $A B$ ， $E F$ 互相垂直， $\overset{⌢}{C E D}$ 和 $\overset{⌢}{C F D}$ 所对的圆心角都为 $12 0^{°}$ ，且 $\overset{⌢}{C E D} = \overset{⌢}{C F D}$ .现随机地向该图形内掷一枚小针，记针尖落在 $\overset{⌢}{C E D}$ 和 $\overset{⌢}{C F D}$ 所围封闭区域内的概率为 $P_{1}$ ，针尖落在 $⊙ O$ 内的概率为 $P_{2}$ ，则 $\frac{P_{1}}{P_{2}} =$ .

查看试题解析
26. 已知a、b、c、满足 $\frac{b}{a + c} = \frac{a}{c + b} = \frac{c}{a + b} = k$ ，从下列四点：① $(1 ， \frac{1}{2})$ ；②(2，1)；③ $(1 ， - \frac{1}{2})$ ；④(1，﹣1)，中任意取一点恰好在正比例函数y＝kx图象上的概率是.

查看试题解析