备考2023年中考数学嘉兴卷变式阶梯训练：第10题

试卷更新日期：2023-04-15 类型：三轮冲刺

进入出卷网下载

一、原题

1. 已知点A（a，b），B（4，c）在直线y＝kx＋3（k为常数，k≠0）上，若ab的最大值为9，则c的值为（）

A、1 B、 $\frac{3}{2}$ C、2 D、 $\frac{5}{2}$

查看试题解析

二、基础

2. 已知二次函数y₁＝mx²+nx﹣3（m≠0）经过点(2，﹣3).不论m取何实数，若直线y₂＝m²x+k总经过y₁的顶点，则k的取值可以是（）

A、﹣3 B、﹣1 C、0 D、2

查看试题解析
3. 若一次函数y=（a+1）x+a的图象过第一、三、四象限，则二次函数 $y = a x^{2} - a x$ （　　）

A、有最大值 B、有最大值﹣ C、有最小值 D、有最小值﹣

查看试题解析
4. 已知M、N两点关于y轴对称，且点M在反比例函数y= $\frac{1}{2 x}$ 的图象上，点N在一次函数 y=x+3的图象上，设点M的坐标为（a，b），则二次函数y=abx²+(a+b)x（）

A、有最小值，且最小值是- $\frac{9}{2}$ B、有最大值，且最大值是- $\frac{9}{2}$ C、有最大值，且最大值是 $\frac{9}{2}$ D、有最小值，且最小值是 $\frac{9}{2}$

查看试题解析
5. 已知二次函数 $y = a x^{2} - 2 a x + a + 2 (a \neq 0)$ ，若 $- 1 \leq x \leq 2$ 时，函数的最大值与最小值的差为4，则a的值为（）

A、1 B、-1 C、 $\pm 1$ D、无法确定

查看试题解析
6. 已知非负数 $a ， b ， c$ ，满足 $a - b = 2$ 且 $c + 3 a = 9$ ，设 $y = a^{2} + b + c$ 的最大值为 $m$ ，最小值为 $n$ ，则 $m - n$ 的值是（）

A、1 B、2 C、3 D、4

查看试题解析
7. 已知二次函数y=（x-m+2）（x+m-4）+n，其中m，n为常数，则（）

A、m>1，n<0时，二次函数的最小值大于0 B、m=1，n>0时，二次函数的最小值大于0 C、m<1，n>0时，二次函数的最小值小于0 D、m=1，n<0时，二次函数的最小值小于0

查看试题解析
8. 二次函数y=ax²+bx+c（a≠0）的图象如图所示，则下列命题中正确的是（）

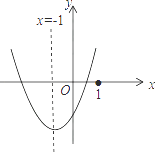A、a＞b＞c B、一次函数y=ax+c的图象不经第四象限 C、m（am+b）+b＜a（m是任意实数） D、3b+2c＞0

查看试题解析

三、进阶

9. 已知二次函数 $y = a x^{2} + 2 x + 1$ （a为实数，且 $a < 0$ ），对于满足 $0 \leq x \leq x_{0}$ 的任意一个x的值，都有 $- 3 \leq y \leq 3$ ，则 $x_{0}$ 的最大值为（）

A、 $2 \sqrt{3} - 2$ B、 $2 \sqrt{3} + 2$ C、 $2 \sqrt{5} + 2$ D、 $2 \sqrt{5} - 2$

查看试题解析
10. 如图，点A（1，16），B（2，12），C（3，8），D（4，4）均在函数l图象上，P为该函数在第一象限内图象上一点，PE⊥x轴于点E，当△OEP的面积取最大值时，OE的长为（）

A、1.5 B、2.5 C、3.5 D、4.5

查看试题解析
11.
如图，抛物线经过A(1，0)，B(4，0)，C(0，-4)三点，点D是直线BC上方的抛物线上的一个动点，连结DC，DB，则△BCD的面积的最大值是（）

A、7 B、7.5 C、8 D、9

查看试题解析
12. 如图，过点C（1，2）分别作x轴、y轴的平行线，交直线y=-x+6于A，B两点，若反比例函数 $y = \frac{k}{x}$ （x＞0）的图像与△ABC有公共点，则k的取值范围是（）

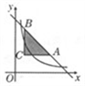A、2≤k≤8 B、2≤k≤9 C、2≤k≤5 D、5≤k≤8

查看试题解析
13. 规定 $m a x {a ， b} = {\begin{array}{l} a (a \geq b) \\ b (a \leq b) \end{array}$ ，若函数 $y = m a x {- 2 x + 1 ， x^{2} - 2 x - 3}$ ，则该函数的最小值为（）

A、 $- 3$ B、 $- 2$ C、2 D、5

查看试题解析
14. 直角坐标系 $x o y$ 中，一次函数 $y = k x + b (k b \neq 0)$ 的图象过点 $(2 ， k b)$ ，且 $b \geq 4$ ，与 $x$ 轴， $y$ 轴分别交于 $A$ ， $B$ 两点.设 $△ A B O$ 的面积为 $S$ ，则 $S$ 的最小值是（）

A、4 B、3 C、2 D、1

查看试题解析
15. 已知一次函数y=ax+b的图象过点（﹣2，1），则关于抛物线y=ax²﹣bx+3的三条叙述：其中所有正确叙述的个数是（）
①过点（2，1），②对称轴可以是x=1，③当a＜0时，其顶点的纵坐标的最小值为3．

A、0 B、1 C、2 D、3

查看试题解析
16. 已知 $y_{1}$ ， $y_{2}$ 均为关于x的函数，当 $x = a$ 时，函数值分别为 $A_{1}$ ， $A_{2}$ ，若对于实数a，当 $0 < a < 1$ 时，都有 $- 1 < A_{1} - A_{2} < 1$ ，则称 $y_{1}$ ， $y_{2}$ 为亲函数，则以下函数 $y_{1}$ 和 $y_{2}$ 是亲函数的是（）

A、 $y_{1} = x^{2} + 1$ ， $y_{2} = - \frac{1}{x}$ B、 $y_{1} = x^{2} + 1$ ， $y_{2} = 2 x - 1$ C、 $y_{1} = x^{2} - 1$ ， $y_{2} = - \frac{1}{x}$ D、 $y_{1} = x^{2} - 1$ ， $y_{2} = 2 x - 1$

查看试题解析

四、突破

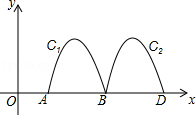
17. 已知函数 $y = x^{2} - 4 a x + 5$ （a为常数），当 $x ⩾ 4$ 时，y随x增大而增大. $P (x_{1}, y_{1}), Q (x_{2}, y_{2})$ 是该函数图象上的两点，对任意的 $2 a - 1 ⩽ x_{1} ⩽ 5$ 和 $2 a - 1 ⩽ x_{2} ⩽ 5$ ， $y_{1}, y_{2}$ 总满足 $y_{1} - y_{2} ⩽ 5 + 4 a^{2}$ ，则实数a的取值范围是（）

A、 $- 1 ⩽ a ⩽ 2$ B、 $1 ⩽ a ⩽ 2$ C、 $2 ⩽ a ⩽ 3$ D、 $2 ⩽ a ⩽ 4$

查看试题解析
18. 若二次函数y＝ax²＋bx－1的最小值为－3，则方程|ax²＋bx－1|＝2的不相同实数根的个数是（）

A、2 B、3 C、4 D、5

查看试题解析
19. 已知函数y＝ ${\begin{array}{l} x^{2} - x (x ⩾ 0) \\ - x^{2} - x (x < 0) \end{array}$ ，当a≤x≤b时，﹣ $\frac{1}{4}$ ≤y≤ $\frac{1}{4}$ ，则b﹣a的最大值为（）

A、1 B、 $\sqrt{2}$ +1 C、 $\frac{2 \sqrt{2} + 1}{2}$ D、 $\frac{\sqrt{2}}{2}$

查看试题解析
20. 如图，抛物线y=﹣2x²+8x﹣6与x轴交于点A、B，把抛物线在x轴及其上方的部分记作C₁ ，将C₁向右平移得C₂ ， C₂与x轴交于点B，D．若直线y=x+m与C₁、C₂共有3个不同的交点，则m的取值范围是（）

A、 $- 2 < m < \frac{1}{8}$ B、 $- 3 < m < - \frac{7}{4}$ C、 $- 3 < n < - 2$ D、 $- 3 < m < - \frac{15}{8}$

查看试题解析
21. 在平面直角坐标系xOy中，已知点M，N的坐标分别为 $(- 1 ， 2)$ ， $(2 ， 1)$ ，若抛物线 $y = a x^{2} - x + 2 (a \neq 0)$ 与线段MN有两个不同的交点，则a的取值范围是（）

A、 $a \leq - 1 ，或 \frac{1}{4} \leq a < \frac{1}{3}$ B、 $\frac{1}{4} \leq a < \frac{1}{3}$ C、 $a \leq \frac{1}{4} 或 a > \frac{1}{3}$ D、 $a \leq - 1 或 a \geq \frac{1}{4}$

查看试题解析
22. 如图，已知二次函数y＝﹣ $\frac{5}{4}$ （x+1）（x﹣4）的图象与x轴交于A、B两点（点A在点B的左侧），与y轴交于点C，P为该二次函数在第一象限内的一点，连接AP，交BC于点K，则 $\frac{A P}{P K}$ 的最小值为（）

A、 $\frac{9}{4}$ B、2 C、 $\frac{7}{4}$ D、 $\frac{5}{4}$

查看试题解析
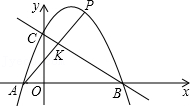23. 在平面直角坐标系中，如果点P的横坐标和纵坐标相等，则称点P为和谐点．例如点（1，1），（﹣ $\frac{1}{3}$ ， ﹣ $\frac{1}{3}$ ），（﹣ $\sqrt{2}$ ， ﹣ $\sqrt{2}$ ），…，都是和谐点．若二次函数y＝ax²+4x+c（a≠0）的图象上有且只有一个和谐点（ $\frac{3}{2}$ ， $\frac{3}{2}$ ），当0≤x≤m时，函数y＝ax²+4x+c﹣ $\frac{3}{4}$ （a≠0）的最小值为﹣3，最大值为1，m的取值范围是（）

A、m≤4 B、m≥2 C、2≤m≤4 D、2＜m＜4

查看试题解析