备考2023年中考数学嘉兴卷变式阶梯训练:第4题
试卷更新日期:2023-04-15 类型:三轮冲刺
一、原题
-
1. 如图,在⊙O中,∠BOC=130°,点A在 上,则∠BAC的度数为( )
 A、55° B、65° C、75° D、130°
A、55° B、65° C、75° D、130°二、基础
-
2. 如图,是的外接圆, , 则的度数为( )
 A、55° B、25° C、105° D、110°3. 如图,⊙O是ABC的外接圆, , 则的大小为( ).
A、55° B、25° C、105° D、110°3. 如图,⊙O是ABC的外接圆, , 则的大小为( ). A、 B、 C、 D、4. 如图,为的直径, , 为上的两点,若 , 则的度数为( )
A、 B、 C、 D、4. 如图,为的直径, , 为上的两点,若 , 则的度数为( ) A、 B、 C、 D、5. 如图,线段是的直径,如果 , 那么的度数是( )
A、 B、 C、 D、5. 如图,线段是的直径,如果 , 那么的度数是( )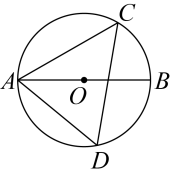 A、 B、 C、 D、6. 如图,在⊙O中,AB是直径,CD是弦.若∠BCD=44°,则∠ABD=( )
A、 B、 C、 D、6. 如图,在⊙O中,AB是直径,CD是弦.若∠BCD=44°,则∠ABD=( )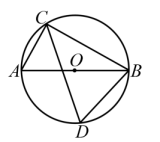 A、40° B、44° C、45° D、46°7. 如图,点 , , , 在⊙O上,是的直径,若 , 则的度数为( )
A、40° B、44° C、45° D、46°7. 如图,点 , , , 在⊙O上,是的直径,若 , 则的度数为( ) A、 B、 C、 D、8. 如图,是直径, , 则∠D为( )
A、 B、 C、 D、8. 如图,是直径, , 则∠D为( )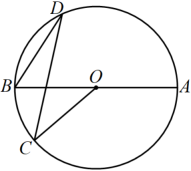 A、 B、 C、 D、9. 如图,是的直径, , 是上的两点,且 , 则的度数为( )
A、 B、 C、 D、9. 如图,是的直径, , 是上的两点,且 , 则的度数为( )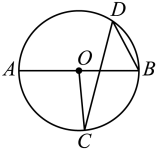 A、42° B、84° C、90° D、96°
A、42° B、84° C、90° D、96°三、进阶
-
10. 、、是上的点,若 , 则的度数为( )A、或 B、 C、 D、或11. 如图,在中, , 点分别是优弧与劣弧上的动点,则的度数不可能是( )
 A、 B、 C、 D、12. 如图,是的直径,弦交于点E,连接 . 若 , 则的度数是( )
A、 B、 C、 D、12. 如图,是的直径,弦交于点E,连接 . 若 , 则的度数是( ) A、 B、 C、 D、13. 如图,点D是的中点,弦与交于点E, , 若 , 则的度数为( )
A、 B、 C、 D、13. 如图,点D是的中点,弦与交于点E, , 若 , 则的度数为( ) A、 B、 C、 D、14. 如图,AB是的直径,点C在上,连接AC、BC,过点O作交于点D,点C、D在AB的异侧.若 , 则的度数是( )
A、 B、 C、 D、14. 如图,AB是的直径,点C在上,连接AC、BC,过点O作交于点D,点C、D在AB的异侧.若 , 则的度数是( ) A、66° B、67° C、57° D、48°15. 如图所示,△ABC的三个顶点在⊙O上,D是上的点,E是上的点,若∠BAC=50°.则∠D+∠E=( )
A、66° B、67° C、57° D、48°15. 如图所示,△ABC的三个顶点在⊙O上,D是上的点,E是上的点,若∠BAC=50°.则∠D+∠E=( ) A、220° B、230° C、240° D、250°16. 如图,AB是⊙O的直径,CD是⊙O的弦,连接AC,AD,BD.若∠CAB=36°,则∠ADC的度数为( )
A、220° B、230° C、240° D、250°16. 如图,AB是⊙O的直径,CD是⊙O的弦,连接AC,AD,BD.若∠CAB=36°,则∠ADC的度数为( ) A、72° B、54° C、45° D、36°17. 如图,四边形内接于 , , , 则( )
A、72° B、54° C、45° D、36°17. 如图,四边形内接于 , , , 则( )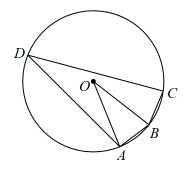 A、 B、 C、 D、无法确定18. 如图, 一块直角三角板的角的顶点落在上, 两边分别交于两点, 连结 , 则的度数是( )
A、 B、 C、 D、无法确定18. 如图, 一块直角三角板的角的顶点落在上, 两边分别交于两点, 连结 , 则的度数是( ) A、 B、 C、 D、19. 以O为中心点的量角器与直角三角板按如图方式摆放,量角器的0刻度线与斜边重合.点D为斜边上一点,作射线交弧于点E,如果点E所对应的量角器上的读数为 , 那么的大小为( )
A、 B、 C、 D、19. 以O为中心点的量角器与直角三角板按如图方式摆放,量角器的0刻度线与斜边重合.点D为斜边上一点,作射线交弧于点E,如果点E所对应的量角器上的读数为 , 那么的大小为( )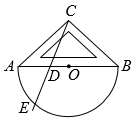 A、 B、 C、 D、
A、 B、 C、 D、四、突破
-
20. 如图,在给定的锐角三角形ABC中,∠BAC=60°,D是边BC上的一个动点,以AD为直径作⊙O分别交边AB,AC于点E,F,连接EF,当点D从点B运动到点C的过程中,线段EF的长度的大小变化情况是( )
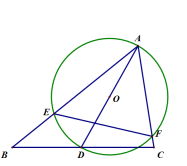 A、一直不变 B、一直减少 C、先减小后增大 D、先增大后减小21. 如图,四边形ABCD中,对角线AC,BD交于点E. 若 , 则下列结论中正确的是( )
A、一直不变 B、一直减少 C、先减小后增大 D、先增大后减小21. 如图,四边形ABCD中,对角线AC,BD交于点E. 若 , 则下列结论中正确的是( )
①
②与的周长比为③
④S△ABE·S△DCE=S△ADE·S△BCEA、③④ B、①②③ C、①②④ D、①②③④22. 如图,等腰内接于圆O,直径 , D是圆上一动点,连接 , , 且交于点G.下列结论:①平分;②;③当 , 四边形的面积为;④当时,四边形的周长最大,正确的有( ) A、①② B、②③ C、①②④ D、①③④23. 如图,AB是半圆O的直径,点C、E是半圆上的动点(不与点A、B重合),且= , 射线AE,BC交于点F,M为AF中点,G为CM上一点,作∠GON= , 交BC于点N,则点C在从点A往点B运动的过程中,四边形CGON的面积( )
A、①② B、②③ C、①②④ D、①③④23. 如图,AB是半圆O的直径,点C、E是半圆上的动点(不与点A、B重合),且= , 射线AE,BC交于点F,M为AF中点,G为CM上一点,作∠GON= , 交BC于点N,则点C在从点A往点B运动的过程中,四边形CGON的面积( )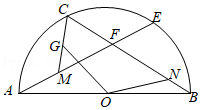 A、先变大后变小 B、先变小后变大 C、保持不变 D、一直减小24. 我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形,根据定义:①等边三角形一定是奇异三角形;②在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,则a:b:c=1::2;③如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.则△ACE是奇异三角形;④在③的条件下,当△ACE是直角三角形时,∠AOC=120°,其中,说法正确的有( )
A、先变大后变小 B、先变小后变大 C、保持不变 D、一直减小24. 我们定义:两边平方和等于第三边平方的2倍的三角形叫做奇异三角形,根据定义:①等边三角形一定是奇异三角形;②在Rt△ABC中,∠C=90°,AB=c,AC=b,BC=a,且b>a,若Rt△ABC是奇异三角形,则a:b:c=1::2;③如图,AB是⊙O的直径,C是⊙O上一点(不与点A、B重合),D是半圆的中点,C、D在直径AB的两侧,若在⊙O内存在点E,使AE=AD,CB=CE.则△ACE是奇异三角形;④在③的条件下,当△ACE是直角三角形时,∠AOC=120°,其中,说法正确的有( ) A、①② B、①③ C、②④ D、③④
A、①② B、①③ C、②④ D、③④
-