备考2023年中考数学温州卷变式阶梯训练:第24题
试卷更新日期:2023-04-15 类型:三轮冲刺
一、原题
-
1. 如图1, AB 为半圆O的直径,C为 BA 延长线上一点, CD 切半圆于点D, BE⊥CD ,交 CD 延长线于点E,交半圆于点F,已知BC=5,BE=3.点P,Q分别在线段 AB、BE上(不与端点重合),且满足 .设BQ=x,CP=y.
 (1)、求半圆O的半径.(2)、求y关于x的函数表达式.(3)、如图2,过点P作 PR⊥CE 于点R,连结 PQ、RQ.
(1)、求半圆O的半径.(2)、求y关于x的函数表达式.(3)、如图2,过点P作 PR⊥CE 于点R,连结 PQ、RQ.①当 △PQR 为直角三角形时,求x的值.
②作点F关于 QR 的对称点 F' ,当点 F'落在 BC上时,求 的值.
二、基础
-
2. 如图,在RtABC中, , 点O为BC上一点,以O为圆心、OB为半径的⊙切AC于点D,连接OA、BD、OA与BD相交于点E.
 (1)、求证:BD平分;(2)、若 , ⊙的半径为10,求OE的长.3. 如图,从 外一点 引割线 , 与 相切于点 ,连接 , , .
(1)、求证:BD平分;(2)、若 , ⊙的半径为10,求OE的长.3. 如图,从 外一点 引割线 , 与 相切于点 ,连接 , , .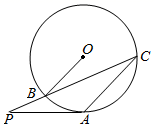 (1)、求证: ;(2)、已知 , ,求 的长.4. 如图,AB为⊙O的直径,C为圆上的一点,D为劣弧的中点,过点D作⊙O的切线与AC的延长线交于点P,与AB的延长线交于点F,AD与BC交于点E.
(1)、求证: ;(2)、已知 , ,求 的长.4. 如图,AB为⊙O的直径,C为圆上的一点,D为劣弧的中点,过点D作⊙O的切线与AC的延长线交于点P,与AB的延长线交于点F,AD与BC交于点E.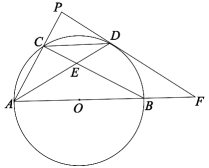 (1)、求证:;(2)、若⊙O的半径为 , DE=1,求AE的长度;(3)、在(2)的条件下,求的面积.5. 如图,在 中,直径 与弦 互相垂直,垂足为H,点E是弧 上一点,连接 ,过点E作直线 交 的延长线于点M,交 的延长线于点G,连接 交 于点F,且 .
(1)、求证:;(2)、若⊙O的半径为 , DE=1,求AE的长度;(3)、在(2)的条件下,求的面积.5. 如图,在 中,直径 与弦 互相垂直,垂足为H,点E是弧 上一点,连接 ,过点E作直线 交 的延长线于点M,交 的延长线于点G,连接 交 于点F,且 . (1)、求证: 是 的切线;(2)、若 ,求证: ;(3)、在(2)的条件下,若 , ,求 的值.6. 如图,圆心在坐标原点的⊙O , 与坐标轴的交点分别为A、B和C、D . 弦CM交OA于P , 连结AM , 已知tan∠PCO= ,PC、PM是方程x2﹣px+20=0的两根.
(1)、求证: 是 的切线;(2)、若 ,求证: ;(3)、在(2)的条件下,若 , ,求 的值.6. 如图,圆心在坐标原点的⊙O , 与坐标轴的交点分别为A、B和C、D . 弦CM交OA于P , 连结AM , 已知tan∠PCO= ,PC、PM是方程x2﹣px+20=0的两根.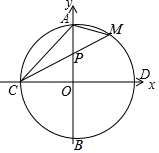 (1)、求C点的坐标;(2)、写出直线CM的函数解析式;(3)、求△AMC的面积.7. 如图,在中, , O为上一点,经过点A的分别交 , 于点E,F,与相切于点D,连接 , 相交于点G.
(1)、求C点的坐标;(2)、写出直线CM的函数解析式;(3)、求△AMC的面积.7. 如图,在中, , O为上一点,经过点A的分别交 , 于点E,F,与相切于点D,连接 , 相交于点G. (1)、求证:平分;(2)、求证:;(3)、若 , , 求的长.8. 如图, 是以 为直径的 上一点,过点 的切线 交 的延长线于点 ,过点 作 交 的延长线于点 ,垂足为点 .
(1)、求证:平分;(2)、求证:;(3)、若 , , 求的长.8. 如图, 是以 为直径的 上一点,过点 的切线 交 的延长线于点 ,过点 作 交 的延长线于点 ,垂足为点 .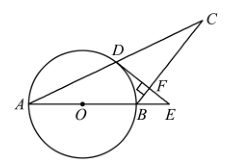 (1)、求证: ;(2)、若 的直径 为9, .
(1)、求证: ;(2)、若 的直径 为9, .①求线段 的长;
②求线段 的长.
9. 如图,四边形 内接于 , 为 的直径, 是 的切线, 交 的延长线于点 ,过点 作 于点 ,连接 交 于点 . (1)、求证: ;(2)、若 , ,求 的半径;(3)、在(2)的条件下,求四边形 的面积.10. 如图,⊙O的直径AB垂直于弦CD于点E, , ,点P是CD延长线上异于点D的一个动点,连结AP交⊙O于点Q,连结CQ交AB于点F,则点F的位置随着点P位置的改变而改变.
(1)、求证: ;(2)、若 , ,求 的半径;(3)、在(2)的条件下,求四边形 的面积.10. 如图,⊙O的直径AB垂直于弦CD于点E, , ,点P是CD延长线上异于点D的一个动点,连结AP交⊙O于点Q,连结CQ交AB于点F,则点F的位置随着点P位置的改变而改变.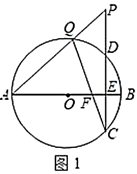
 (1)、如图1,当 时,求 的值;(2)、如图2,连结AC,DQ,在点P运动过程中,设 , .
(1)、如图1,当 时,求 的值;(2)、如图2,连结AC,DQ,在点P运动过程中,设 , .①求证: ;
②求y与x之间的函数关系式.
11. 已知:△ABC内接于⊙O,∠BAC的角平分线AD交⊙O于点D.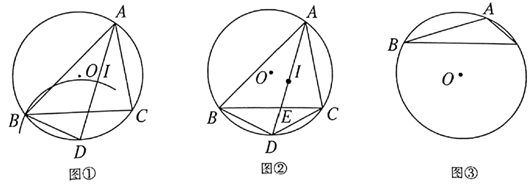 (1)、如图①,以点D为圆心,DB长为半径作弧,交AD于点I.求证:点I是△ABC的内心;(2)、如图②,在(1)的条件下,若AD与BC交于点E.求证: ;(3)、探究:如图③,△ABC内接于⊙O,若BC=8,∠BAC=120°,求△ABC内切圆半径的最大值.12. 如图,已知扇形AOB的半径 , ,点C,D分别在半径OA,OB上(点C不与点A重合),连结CD.
(1)、如图①,以点D为圆心,DB长为半径作弧,交AD于点I.求证:点I是△ABC的内心;(2)、如图②,在(1)的条件下,若AD与BC交于点E.求证: ;(3)、探究:如图③,△ABC内接于⊙O,若BC=8,∠BAC=120°,求△ABC内切圆半径的最大值.12. 如图,已知扇形AOB的半径 , ,点C,D分别在半径OA,OB上(点C不与点A重合),连结CD. (1)、当 , 时,求OC的长.(2)、点P是弧AB上一点, .
(1)、当 , 时,求OC的长.(2)、点P是弧AB上一点, .①当点D与点B重合,点P为弧AB的中点时,求证: .
②当 , 时,求 的值.
三、困难
-
13. 如图,点O是△ABC中AB边上一点,以点O为圆心,OA的长为半径作⊙O,⊙O恰好经过点C,且与边BC,AB分别交于E,F两点.连接AE,过点E作⊙O的切线,交线段BF于点M,交AC的延长线于点N,且EM=BM,EB=AO.
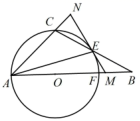 (1)、求 的度数;(2)、求证: ;(3)、若 ,求 的面积.14. 如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E.
(1)、求 的度数;(2)、求证: ;(3)、若 ,求 的面积.14. 如图,已知P为锐角∠MAN内部一点,过点P作PB⊥AM于点B,PC⊥AN于点C,以PB为直径作⊙O,交直线CP于点D,连接AP,BD,AP交⊙O于点E. (1)、求证:∠BPD=∠BAC.(2)、连接EB,ED,当 tan∠MAN=2 AB=时,在点P的整个运动过程中.
(1)、求证:∠BPD=∠BAC.(2)、连接EB,ED,当 tan∠MAN=2 AB=时,在点P的整个运动过程中.①若∠BDE=45°,求PD的长.
②若ΔBED为等腰三角形,求直接写出所有满足条件的BD的长.
(3)、连接OC,EC,OC交AP于点F,当tan∠MAN=1,OC∥BE时,记ΔOFPP的面积为S1 , ΔCFE 的面积为S2 , 请求出的值.15. 如图,在 中, ,以 为直径的 交 于点 ,过点 作 的切线交 于点 . (1)、求证: .(2)、填空:
(1)、求证: .(2)、填空:①当 时,四边形 为正方形;
②当 时,四边形 为菱形.
16. 如图,已知 , 是 的直径, , 与 的边 , 分别交于点 , ,连接 并延长,与 的延长线交于点 , .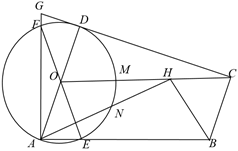 (1)、求证: 是 的切线;(2)、若 ,求 的值;(3)、在(2)的条件下,若 的平分线 交 于点 ,连接 交 于点 ,求 的值.17. 如图1,在Rt△ABC中,∠C=90°,BC=3,AB=5,点P为AC上一点,PD⊥AB于点D,连结PB,以PD为直径的圆交BP于点E,交AC于点F,连结DE,DF,EF.
(1)、求证: 是 的切线;(2)、若 ,求 的值;(3)、在(2)的条件下,若 的平分线 交 于点 ,连接 交 于点 ,求 的值.17. 如图1,在Rt△ABC中,∠C=90°,BC=3,AB=5,点P为AC上一点,PD⊥AB于点D,连结PB,以PD为直径的圆交BP于点E,交AC于点F,连结DE,DF,EF. (1)、求证:∠DEF=∠ABC.(2)、当△DEF为等腰三角形时,求所有满足条件的AP的长.(3)、如图2,过D作DM∥EF交PB于点M,若点M为PB的中点,则DM . (直接写出答案)18. 已知AC是平行四边形ABCD的一条对角线,且AB=AC,⊙O是 的外接圆,CD与⊙O的另一个交点为E,连结AE.
(1)、求证:∠DEF=∠ABC.(2)、当△DEF为等腰三角形时,求所有满足条件的AP的长.(3)、如图2,过D作DM∥EF交PB于点M,若点M为PB的中点,则DM . (直接写出答案)18. 已知AC是平行四边形ABCD的一条对角线,且AB=AC,⊙O是 的外接圆,CD与⊙O的另一个交点为E,连结AE. (1)、当点E在线段CD上时,如图1.
(1)、当点E在线段CD上时,如图1.①求证: ∽
②若 , 的面积为 ,求⊙O的半径.
(2)、当点E在直线CD上时,过点E作EH⊥AB于H,直线EH与直线BC交于点F. 如图2,若 时,求 的值.19. 如图1,⊙O的弦 , 为 所对优弧上一动点且 , 的外角平分线 交⊙O于点 ,直线 与直线 交于点 .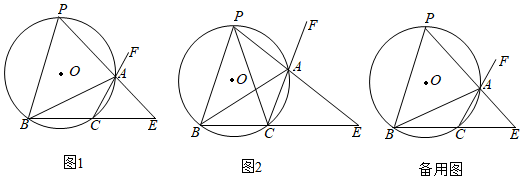 (1)、求证:点 为 的中点;(2)、如图2,求⊙O的半径和 的长;(3)、若 不是锐角三角形,则 的最大值为.20. (提出问题)
(1)、求证:点 为 的中点;(2)、如图2,求⊙O的半径和 的长;(3)、若 不是锐角三角形,则 的最大值为.20. (提出问题)如图1,直径AB垂直弦CD于点E,AB=10,CD=8,点P是CD延长线上异于点D的一个动点,连接AP交⊙O于点Q,连接CQ交AB于点F,则点F的位置随着点P位置的改变而改变.
 (1)、(特殊位置探究)
(1)、(特殊位置探究)
当DP=2时,求tan∠P和线段AQ的长;(2)、(一般规律探究)如图2,连接AC,DQ,在点P运动过程中,设DP=x, y.
①求证:∠ACQ=∠CPA;
②求y与x之间的函数关系式;
(3)、(解决问题)当OF=1时,求△ACQ和△CDQ的面积之比.(直接写出答案)
-