备考2023年中考数学温州卷变式阶梯训练：第22题

试卷更新日期：2023-04-15 类型：三轮冲刺

进入出卷网下载

一、原题

1. 如图，在△ABC 中， AD⊥BC于点D、E、F分别是AC、AB 的中点，O是 DF 的中点， EO 的延长线交线段 BD 于点G，连结 DE、EF、FG．

(1)、求证：四边形 DEFG 是平行四边形．

(2)、当AD=5，tan∠EDC= $\frac{5}{2}$ =时，求 FG 的长．

查看试题解析

二、基础

2. 如图，在 $△ A B C$ 中，点D，E分别是AC，AB的中点，点F是CB延长线上的一点，且 $C F = 3 B F$ ，连接DB，EF．若 $∠ A C B = 90 °$ ， $A C = 12 c m$ ， $D E = 4 c m$ ，

(1)、求证： $D E = B F$ ；

(2)、求四边形DEFB的周长．

查看试题解析
3. 如图，在 $△ A B C$ 中，D、E分别为AB、AC的中点，过点C作 $C F / / B D$ 交DE的延长线于点F．

(1)、求证：四边形BCFD为平行四边形；

(2)、若 $B C = 6$ ，求EF的长．

查看试题解析
4. 如图，在▱ABCD中，点E在边AD上，连接EB并延长至F，使BF＝BE；连接EC并延长至G，使CG＝CE，连接FG，点H为FG的中点，连接DH，AF．

(1)、若∠BAE＝70°，∠DCE＝20°，求∠DEC的度数；

(2)、求证：四边形AFHD为平行四边形．

查看试题解析
5. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ，延长BA到点D，使 $A D = \frac{1}{2} A B$ ，点E、F分别为边BC、AC的中点．

(1)、求证： $D F = B E$ ；

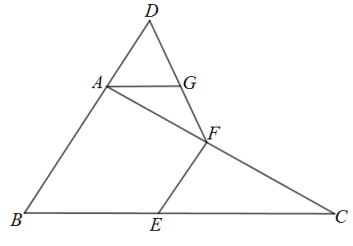(2)、过点A作 $A G ∥ B C$ ，交DF于点G，求证： $A G = D G$ ．

查看试题解析
6. 如图，线段DE与AF分别为△ABC的中位线与中线.

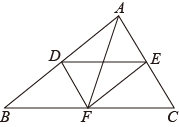(1)、求证：AF与DE互相平分；

(2)、当线段AF与BC满足怎样的数量关系时，四边形ADFE为矩形？请说明理由.

查看试题解析
7. 如图，点D、E、F分别是△ABC的边AB、BC、AC的中点，延长DE至点G，使得DE=EG，连接AE，FG.

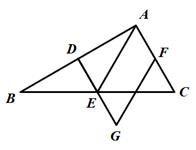(1)、求证：四边形AEGF是平行四边形．

(2)、若∠BAC＝90°，AD＝AC＝ $3$ ，求FG的长．

查看试题解析
8. 如图，点O是△ABC内一点，连接OA、OB、OC，并将AB、OB、OC、AC的中点D、E、F、G依次连接，得到四边形DEFG．

(1)、求证：四边形DEFG是平行四边形；

(2)、若BO上CO，M为EF的中点，且OA＝8，OM＝3，求四边形DEFG的周长．

查看试题解析
9. 如图，四边形ABCD为平行四边形，E为AD上的一点，连接EB并延长，使 $B F = B E$ ，连接EC并延长，使 $C G = C E$ ，连接FG，H为FG的中点，连接DH

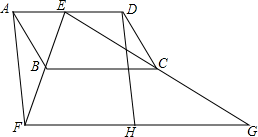(1)、求证：四边形AFHD为平行四边形；

(2)、若 $C B = C E$ ， $∠ E B C = 75 °$ ， $∠ D C E = 10 °$ ，求 $∠ D A B$ 的度数.

查看试题解析

三、进阶

10. 如图，在Rt△ABC中，∠ACB＝90°，D、E分别是边AC、AB的中点，连接CE、DE，过D点作DF∥CE交BC的延长线于F点．

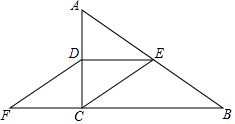(1)、证明：四边形DECF是平行四边形；

(2)、若AB＝13cm，AC＝5cm，求四边形DECF的周长．

查看试题解析
11. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $B C = A C$ ，点 $D$ 是边 $A B$ 的中点.

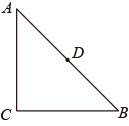(1)、求作一点 $E$ ，使得点 $E$ 与点 $D$ 关于 $A C$ 对称；（要求：尺规作图，保留痕迹，不写作法）

(2)、连接 $C E$ ，请写出线段 $C E$ 、 $B D$ 之间的关系，并证明.

查看试题解析
12. 如图，已知CD为△ABC中线，E为CD上一点，连接AE并延长至点F，使 $E F = A E$ ，连接BF、CF， $C F ∥ A B$ ．

(1)、求证：四边形DBFC是平行四边形．

(2)、设四边形ABFC的面积为S，在不添加任何辅助线的情况下，请写出图中四个面积等于 $\frac{1}{3} S$ 的三角形．

查看试题解析
13. 已知，如图，在平行四边形ABCD中，点G，H分别是AB，CD的中点，点E，F在对角线AC上，且AE=CF．

(1)、求证：四边形EGFH是平行四边形．

(2)、连结BD交AC于点O，若BD=12，AE=EF-CF，求EG的长．

查看试题解析
14. 如图，在 $▱ A B C D$ 中， $A C$ ， $B D$ 相交于点 $O$ ， $A B = A D$ ， $A C = 8$ ， $B D = 6$ ， $C E ∥ B D$ ， $B E ∥ A C$ ，连接 $O E$ ， $B C$ 与 $O E$ 相交于点 $P$ ，连接 $D P$ ．

(1)、求 $A B$ 的长；

(2)、求证： $O E = A D$ ；

(3)、求 $D P$ 的长．

查看试题解析
15. 如图，在Rt⊿ABC中，∠ACB是直角， tan∠B= $\frac{3}{4}$ ，BC=16 cm，点D以2cm/s的速度由点A向点B匀速运动，到达点B即停止，M、N分别是AD、CD的中点，连结MN，设点D的运动时间为t

(1)、求MN的长；

(2)、求点D由点A到点B匀速运动过程中，线段MN所扫过的面积；

(3)、若⊿DMN是等腰三角形时，求t的值．

查看试题解析
16. （问题情境）
如图1，在 $△ A B C$ 中， $A C = B C$ ，D是 $A B$ 边上一点，过点D作 $D E / / B C$ 交 $A C$ 于点E，以D为顶点， $D E$ 为一边作 $∠ E D F = ∠ A C B$ ，使其另一边与 $B C$ 边交于点F， $E F$ 与 $C D$ 交于点G．

(1)、求证：G是 $E F$ 的中点；

(2)、M，N分别是 $A C$ ， $B C$ 的中点，连接 $M N$ ，求证：点G在线段 $M N$ 上；

(3)、（迁移拓展）
如图2，已知D是长为4的线段 $A B$ 上的动点（D不与A，B重合），分别以 $A D$ ， $D B$ 为边在线段 $A B$ 的同侧作等边 $△ A D E$ 和等边 $△ B D F$ ，G为 $E F$ 的中点，连接 $D G$ ．

①请直接写出 $G D$ 的最小值；（不要求写解题过程）

②请写出解题过程中需要的辅助线作法，并在图2中画出相应的辅助线．

查看试题解析

四、突破

17. 如图，经过坐标原点O的直线交反比例函数 $y = \frac{k}{x} (k ＜ 0)$ 的图象于点A（﹣2，3），B．点C是x轴上异于点O的动点，点D与点C关于y轴对称，射线AC交y轴于点E，连结AD，BC，BD．

(1)、①写出点B的坐标．
②求证：四边形ACBD是平行四边形．

(2)、当四边形ACBD是矩形时，求点C的坐标．

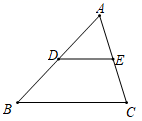
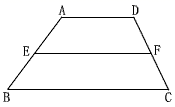
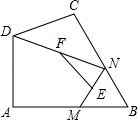(3)、点C在运动过程中，当A，C，E三点中的其中一点到另两点的距离相等时，求 $\frac{O E}{B C}$ 的值．

查看试题解析
18. 如图

(1)、如图，已知△ABC中，D、E分别是AB、AC的中点，求证：DE∥BC，DE= $\frac{1}{2}$ BC.

(2)、利用第（1）题的结论，解决下列问题：
①如图，在四边形ABCD中，AD∥BC，E、F分别是AB、CD的中点，求证：EF∥BC，FE= $\frac{1}{2}$ （AD+BC）

②如图，在四边形ABCD中，∠A＝90°，AB＝3 $\sqrt{3}$ ，AD＝3，点M，N分别在边AB，BC上，点E，F分别为MN，DN的中点，连接EF，求EF长度的最大值.

查看试题解析

19. 教材呈现：浙教版八年级下册数学教材第98页的部分内容：

连结三角形两边中点的线段叫做三角形的中位线.如图，在 $△ A B C$ 中， $D$ ， $E$ 分别是 $A B$ ， $A C$ 的中点， $D E$ 就是 $△ A B C$ 的一条中位线.我们可得到下面三角形的中位线定理：

三角形的中位线平行于第三边，并且等于第三边的一半.

已知：如图， $D E$ 是 $△ A B C$ 的中位线.

求证： $D E / / B C$ 且 $D E = B C$ .

(1)、请根据教材内容，结合图1，写出证明过程：

(2)、如图2，等腰直角三角形

A B C

中，

A C = B C = 2

，

∠ C = 90 °

，点

D

，

E

分别是

A B

，

A C

的中点，将

△ A D E

绕点

A

逆时针旋转一周，点

D

，

E

的对应点分别是

D'

，

E'

，连结

B D'

，设

B D'

的中点为

F

，在旋转过程中，点

D

和点

F

之间的距离会变化吗？若变化，请说明理由，若不变化，请求出这个距离的值；

(3)、在（2）的旋转过程中，连结

C F

如图3，求

∠ B C F

度数的取值范围.

查看试题解析

20. 爱好思考的小实在探究两条直线的位置关系查阅资料时发现，两条中线互相垂直的三角形称为“中垂三角形”，如图1、图2、图3中，AF、BE是△ABC的中线，AF⊥BE于点P，像△ABC这样的三角形均为“中垂三角形”，设BC＝a，AC＝b，AB＝c.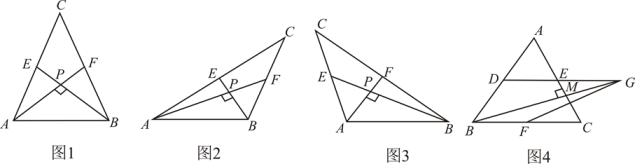

(1)、【特例探究】
①如图1，当tan∠PAB＝1， $c = 4 \sqrt{2}$ 时，a＝， b＝.

②如图2，当∠PAB＝30°，c＝4时，a＝， b＝.

(2)、【归纳证明】
请你观察（1）中的计算结果，猜想 $a^{2}$ 、 $b^{2}$ 、 $c^{2}$ 三者之间的关系，用等式表示出来，并利用图3证明你的结论.

(3)、【拓展证明】
如图4，在△ABC中， $A B = 4 \sqrt{3}$ ， $B C = 2 \sqrt{5}$ ，D、E、F分别是边AB、AC、BC的中点，连结DE并延长至点G，使得GE＝DE，连结BG.若BG⊥AC于点M时，求GF的长.

查看试题解析
21. 某校组织数学兴趣探究活动，爱思考的小实同学在探究两条直线的位置关系查阅资料时发现，两条中线互相垂直的三角形称为“中垂三角形”.如图1、图2、图3中， $A F$ 、 $B E$ 是 $△ A B C$ 的中线， $A F ⊥ B E$ 于点 $P$ ，像 $△ A B C$ 这样的三角形均称为“中垂三角形”.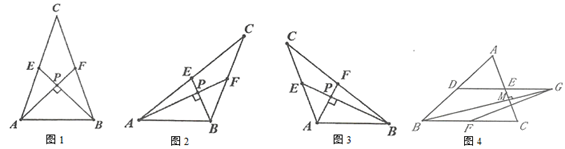

(1)、（特例探究）
如图1，当 $∠ P A B = 45 °$ ， $A B = 6 \sqrt{2}$ 时， $A C =$ ， $B C =$ ；

如图2，当 $\sin ∠ P A B = \frac{1}{2}$ ， $A B = 4$ 时， $A C =$ ， $B C =$ ；

(2)、（归纳证明）
请你观察（1）中的计算结果，猜想 $A B^{2}$ 、 $B C^{2}$ 、 $A C^{2}$ 三者之间的关系，用等式表示出来，并利用图3证明你的结论；

(3)、（拓展证明）
如图4，在 $△ A B C$ 中， $A B = 4 \sqrt{3}$ ， $B C = 2 \sqrt{5}$ ， $D$ 、 $E$ 、 $F$ 分别是边 $A B$ 、 $A C$ $B C$ 的中点，连结 $D E$ 并延长至 $G$ ，使得 $G E = D E$ ，连结 $B G$ ，当 $B G ⊥ A C$ 于点 $M$ 时，求 $G F$ 的长.

查看试题解析