备考2023年中考数学温州卷变式阶梯训练：第21题

试卷更新日期：2023-04-15 类型：三轮冲刺

进入出卷网下载

一、原题

1. 已知反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象的一支如图所示，它经过点（3，-2）．

(1)、求这个反比例函数的表达式，并补画该函数图象的另一支．

(2)、求当 y≤5，且y≠0时自变量x的取值范围．

查看试题解析

二、基础

2. 已知反比例函数 $y = \frac{k}{x}$ 的图象与正比例函数 $y = 2 x$ 的图象交于点 $(2 ， m)$ ，求这个反比例函数的表达式，并在同一平面直角坐标系内，画出这两个函数的图象．

查看试题解析
3. 在平面直角坐标系中，画出函数 $y = \frac{4}{x}$ 的图象.

查看试题解析
4. 已知函数y＝ $\frac{a}{x - 1}$ +b（a、b为常数且a≠0）中，当x＝2时，y＝4；当x＝﹣1时，y＝1.请对该函数及其图象进行如下探究：

(1)、求该函数的解析式，并直接写出该函数自变量x的取值范围；

(2)、请在下列直角坐标系中画出该函数的图象；

(3)、请你在上方直角坐标系中画出函数y＝2x的图象，结合上述函数的图象，写出不等式 $\frac{a}{x - 1}$ +b≤2x的解集.

查看试题解析

5. 有这样一个问题：探究函数y=

\frac{2 x - 6}{x - 2}

的图象与性质．小慧根据学习函数的经验，对函数y=

\frac{2 x - 6}{x - 2}

的图象与性质进行了探究．下面是小慧的探究过程，请补充完成：

(1)、函数y=

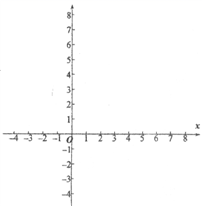\frac{2 x - 6}{x - 2}

的自变量x的取值范围是；

(2)、列出y与x的几组对应值．请直接写出m的值，m=；

x	…	-3	-2	0	1	1.5	2.5	m	4	6	7	…
y	…	2.4	2.5	3	4	6	-2	0	1	1.5	1.6	…

(3)、请在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；

(4)、结合函数的图象，写出该函数的两条性质：

①；

② ．

查看试题解析

6. 某班“数学兴趣小组”对函数 $y = \frac{x}{x - 1}$ 的图象和性质进行了探究，探究过程如下，请补充完整：

(1)、自变量x的取值范围是；

(2)、下表是y与x的几组对应数值：

x … -3 -2 -1 $- \frac{1}{2}$ 0 $\frac{1}{4}$ $\frac{1}{2}$ $\frac{3}{4}$ $\frac{5}{4}$ 2 3 4 …

y … $\frac{3}{4}$ $\frac{2}{3}$ $\frac{1}{2}$ $\frac{1}{3}$ 0 $- \frac{1}{3}$ -1 -3 m 2 $\frac{3}{2}$ $\frac{4}{3}$ …

①写出m的值为；

(3)、当 $\frac{x}{x - 1} > x$ 时，直接写出x的取值范围为.

(4)、结合函数的图象，写出该函数的一条性质：．

查看试题解析

7. 已知

y

是

x

的反比例函数，下表给出了

x

与

y

的一些值．

$x$	…	-4		-2	-1	1		3	4	…
$y$	…		-2			6	3			…

(1)、求出这个反比例函数的表达式；

(2)、根据函数表达式完成上表；

(3)、根据上表，在下图的平面直角坐标系中作出这个反比例函数的图象．

查看试题解析

三、进阶

8. 商场出售一批进价为2元的贺卡，在市场营销中发现此商品日销售单价x (元)与日销售量y (张) 之间有如下关系：

x/元

3

4

5

6

y /张

20

15

12

10

(1)、根据表中的数据在平面直角坐标系中描出实数对(x，y)的对应点；

(2)、猜想并确定y关于x的函数解析式，并画出函数图象；

(3)、设经营此贺卡的日销售利润为W (元)，试求出W关于x的函数解析式，若物价局规定此贺卡的日销售单价最高不能超过10元/张，请你求出当日销售单价x定为多少元时，才能获得最大日销售利润？

查看试题解析

9. 启航同学根据学习函数的经验，对函数

y = \frac{1}{| - x + 1 |}

的图象与性质进行了探究.下面是他的探究过程，请补充完成：

(1)、函数

y = \frac{1}{| - x + 1 |}

的自变量x 的取值范围是；

(2)、列表，找出y 与x 的几组对应值，列表如下：

x	…	-2	-1	0	$\frac{1}{2}$	$\frac{3}{2}$	2	3	..
y	…	a	$\frac{1}{2}$	1	2	2	1	$\frac{1}{2}$	…

其中， a=；

(3)、在平面直角坐标系xOy 中，描出以上表中各对对应值为坐标的点，并画出该函数的图象并写出该函数的一条性质：

查看试题解析

10. 在函数的学习中，我们经历了“确定函数表达式——画函数图象——利用函数图象研究函数性质——利用图像解决问题”的学习过程.我们可以借鉴这种方法探究函数

y = \frac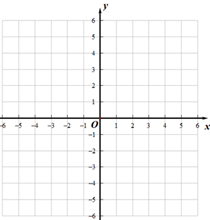{4}{x - 1}

的图像性质.

(1)、补充表格，并画出函数的图象

①列表：

x	…	-3	-1	0	2	3	5	…
y	…	-1	-2	-4	4		1	…

②描点并连线，画图.

(2)、观察图像，写出该函数图象的一个增减性特征：；

(3)、函数

y = \frac{4}{x - 1}

的图像是由函数

y = \frac{4}{x}

的图像如何平移得到的？，其对称中心的坐标为；

(4)、根据上述经验，猜一猜函数

y = \frac{4}{x - 1} + 2

的图像大致位置，结合图像直接写出y≥3时，x的取值范围.

查看试题解析

11. 小邱同学根据学习函数的经验，研究函数y＝

\frac{1}{\sqrt{x - 1} - 1}

的图象与性质.通过分析，该函数y与自变量x的几组对应值如下表，并画出了部分函数图象如图所示.

x	1	$\frac{5}{4}$	$\frac{3}{2}$	$\frac{7}{4}$	3	4	5	6	…
y	﹣1	﹣2	﹣3.4	﹣7.5	2.4	1.4	1	0.8	…

(1)、函数y＝

\frac{1}{\sqrt{x - 1} - 1}

的自变量x的取值范围是；

(2)、在图中补全当1≤x＜2的函数图象；

(3)、观察图象，写出该函数的一条性质：；

(4)、若关于x的方程

\frac{1}{\sqrt{x - 1} - 1}

＝x+b有两个不相等的实数根，结合图象，可知实数b的取值范围是.

查看试题解析

12. 小明根据学习函数的经验，对函数y=x+

\frac{1}{x}

的图象与性质进行了探究．

下面是小明的探究过程，请补充完整：

(1)、函数y=x+

\frac{1}{x}

的自变量x的取值范围是．

(2)、下表列出了y与x的几组对应值，请写出m，n的值：m= ， n=；

…

﹣3

﹣2

﹣1

﹣ $\frac{1}{2}$

﹣ $\frac{1}{3}$

$\frac{1}{3}$

$\frac{1}{2}$

…

﹣ $\frac{10}{3}$

﹣ $\frac{5}{2}$

﹣2

﹣ $\frac{5}{2}$

﹣ $\frac{10}{3}$

$\frac{5}{2}$

$\frac{17}{4}$

…

(3)、如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点，画出该函数的图象；

(4)、结合函数的图象，请完成：

①当y=﹣ $\frac{17}{4}$ 时，x= ．

②写出该函数的一条性质．

③若方程x+ $\frac{1}{x}$ =t有两个不相等的实数根，则t的取值范围是．

查看试题解析

13. 某兴趣小组对函数y＝

\frac{x - 1}{x - 3}

的图象和性质进行探究，请你帮助解决下面问题：

(1)、函数y＝

\frac{x - 1}{x - 3}

中自变量x的取值范围是；

(2)、如表是x、y的几组对应值，则m＝；

x	…	﹣2	﹣1	0	1	2	4	5	6	7	8	…
y	…	$\frac{3}{5}$	m	$\frac{1}{3}$	0	﹣1	3	2	$\frac{5}{3}$	$\frac{3}{2}$	$\frac{7}{5}$	…

(3)、如图，已经画出了该函数图象的一部分，请你画出函数图象的另一部分；

(4)、该函数图象两个分支关于一个点成中心对称，这个点的坐标是；

(5)、若函数y＝

\frac{x - 1}{x - 3}

的图象上有三点A（x₁ ， y₁）、B（x₂ ， y₂）、C（x₃ ， y₃）且x₁＜x₂＜3＜x₃ ，则y₁、y₂、y₃的大小关系是（用“＜”连接）.

查看试题解析

四、突破

14. 函数图象在探索函数的性质中有非常重要的作用，现在就一类特殊的函数展开探索：

y = x + \frac{a}{x}

，探索函数图象和性质过程如下：

$x$	…	-6	-4	-2	-1	-0.5	0.5	1	$n$	4	6	…
$y$	…	$- \frac{20}{3}$	$m$	-4	-5	$- \frac{17}{2}$	$\frac{17}{2}$	5	4	5	$\frac{20}{3}$	…

(1)、上表是该函数

y

与自变量

x

的几组对应值，则

a =

m =

n =

；

(2)、如图，在平面直角坐标系中，已经描出了表中部分点，请根据描出的点画出该函数图象；

(3)、由函数图象，写出该函数的一条性质：；

(4)、请在同一个平面直角坐标系中画出函数

y = 2 x

的图象，并直接写出不等式

x + \frac{a}{x} \leq 2 x

的解集.

查看试题解析

15. 如图，在

R t △ A B C

中

∠ A C B = 9 0^{∘}

，

B C = 4

，

A C = 3 .

点P从点B出发，沿折线

B - C - A

运动，当它到达点A时停止，设点P运动的路程为

x .

点Q是射线CA上一点，

C Q = \frac{6}{x}

，连接

B Q .

设

y_{1} = S_{△ C B Q}

，

y_{2} = S_{△ A B P}

(1)、求出

y_{1}

，

y_{2}

与x的函数关系式，并注明x的取值范围；

(2)、补全表格中

y_{1}

的值；

x	1	2	3	4	6
$y_{1}$	▲	▲	▲	▲	▲

以表中各组对应值作为点的坐标，在直角坐标系内描出相应的点，并在x的取值范围内画出 $y_{1}$ 的函数图象：

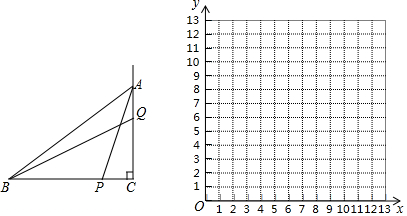(3)、在直角坐标系内直接画出

y_{2}

函数图象，结合

y_{1}

和

y_{2}

的函数图象，求出当

y_{1} < y_{2}

时，x的取值范围.

查看试题解析

16. 某班数学兴趣小组对函数

y = \frac{6}{| x |}

的图象和性质将进行了探究，探究过程如下，请补充完整.

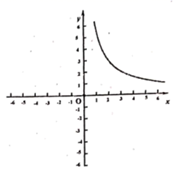(1)、自变量

x

的取值范围是除0外的全体实数，

x

与

y

的几组对应值列表如下：

$x$	…	$- 6$	$- 3$	$- 2$	$- 1$	1	2	3	6	…
$y$	…	1	2	$m$	6	1	3	2	1	…

其中， $m =$ .

(2)、根据上表数据，在如图所示的平面直角坐标系中描点并画出了函数图象的一部分，请画出该函数图象的另一部分.

(3)、观察函数图象，写出一条函数性质.

(4)、进一步探究函数图象发现：

①函数图象与 $x$ 轴交点情况是，所以对应方程 $\frac{6}{| x |} = 0$ 的实数根的情况是.

②方程 $\frac{6}{| x |} = 2$ 有个实效根；

③关于 $x$ 的方程 $\frac{6}{| x |} = a$ 有2个实数根， $a$ 的取值范围是.

查看试题解析

17. 九年级某数学兴趣小组在学习了反比例函数的图象和性质后，进一步研究了函数 $y = \frac{2}{| x |}$ 的图像与性质，其探究过程如下：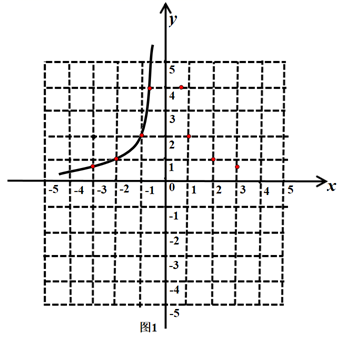

(1)、绘制函数图象，如图1
①列表；下表是x与y的几组对应值，其中 m= ；

②描点：根据表中各组对应值(x，y)在平面直角坐标系中描出了各点；

③连线：用平滑的曲线顺次连接各点，画出了部分图像，请你把图像补充完整；

(2)、通过观察图1，写出该函数的两条性质：①；②；

(3)、①观察发现：如图2，若直线y=2交函数 $y = \frac{2}{| x |}$ 的图像于A，B两点，连接OA，过点B作BC//OA交x轴于点C，则S_OABC=；
②探究思考：将①的直线y=2改为直线y=a(a>0)，其他条件不变，则S_OABC=；

③类比猜想：若直线y=a(a>0)交函数 $y = \frac{k}{| x |} (k > 0)$ 的图像于A，B两点，连接OA，过点B作BC//OA交x轴于C，则 S_OABC= ；

查看试题解析

x/元	3	4	5	6
y /张	20	15	12	10