备考2023年中考数学温州卷变式阶梯训练：第20题

试卷更新日期：2023-04-15 类型：三轮冲刺

进入 出卷网 下载

一、第二十题原题

  • 1. 如图， BD 是 △ABC的角平分线， DE∥BC ，交 AB 于点E．

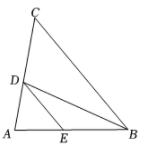    (1)、求证： ∠EBD=∠EDB ．
    (2)、当AB=AC时，请判断 CD 与ED的大小关系，并说明理由．

    查看试题解析

二、第二十题基础

  • 2. 如图，BD是△ABC的角平分线，DE∥BC ， 交AB于点E ．

    (1)、若∠A=45° ， ∠BDC=70° ， 求∠BED的度数；
    (2)、若∠A−∠ABD=15° ， ∠EDC=66° ， 求∠A的度数．

    查看试题解析

  • 3. 如图，在△ABC中，∠ABC的平分线BE交AC于点E ， 过点E作DE∥BC交AB于点D ， 过点D作DF∥BE交AC于点F.

    (1)、求证：DF是∠ADE的平分线；
    (2)、若 ∠BED=28° ， 若∠ACB=81° ，  求∠AFD的度数.

    查看试题解析

  • 4. 已知，如图，在△ABC中，∠C＝ 90°，AD平分∠BAC交BC于D，过D作DE∥AC交AB于E．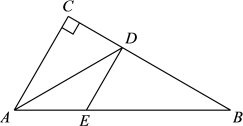

    (1)、求证：AE＝DE；
    (2)、如果AC＝3，AD=23 ， 求AE的长．

    查看试题解析

  • 5. 如图，在△ABC中，AB=AC，D是BC边上的中点，连结AD，BE平分∠ABC交AC于点E.

    (1)、若∠C=36°，求∠BAD的度数；
    (2)、过点E作EF∥BC交AB于点F，求证：FB=FE.

    查看试题解析

  • 6. 如图，在△ABC中，∠A＝90°，CD平分∠ACB交AB于点D，过点D作DE∥BC交AC于点E.

    (1)、若∠B＝40°，求∠CDE的度数.
    (2)、若DE＝4，试添加一个条件，并求出BC的长度.

    查看试题解析

  • 7. 如图，在四边形ABCD中，点E，F分别在边AB，CD上，连结EC，EF，EC平分∠FEB，EF∥BC.

    (1)、求证：EB＝BC.
    (2)、若AD∥EF，DF＝FC，请判断AE与BC的大小关系，并说明理由.

    查看试题解析

  • 8. 如图，在△ABC中，AB=AC ， BE是△ABC的角平分线，EF∥BC交AB于点F.△ABC的一个外角∠ACD的平分线与BE的延长线交于点G.

    (1)、求证：BF=EF；
    (2)、若∠A=80° ， 求∠G的大小.

    查看试题解析

  • 9. 如图，在四边形ABCD中，AB∥CD ， ∠ABC的平分线交CD的延长线于点E，F是BE的中点，连接CF并延长交AD于点G．

    (1)、求证：BC=EC；
    (2)、若∠ADE=110° ， ∠ABC=52° ， 求∠CGD的度数．

    查看试题解析

  • 10. 如图，直线MN∥PQ，直线AB分别与MN，PQ相交于点A，B.

    (1)、利用尺规作∠NAB的平分线与PQ交于点C；
    (2)、若∠ABP=70°，求∠ACB的度数.

    查看试题解析

三、第二十题进阶

  • 11. 如图，AB∥CD，点E为两直线之间的一点.

    (1)、如图1，若∠BAE＝30°，∠DCE＝20°，则∠AEC＝；

    如图1，若∠BAE＝α，∠DCE＝β，则∠AEC＝；

    (2)、如图2，试说明，∠BAE+∠AEC+∠ECD＝360°；
    (3)、如图3，若∠BAE的平分线与∠DCE的平分线相交于点F，判断∠AEC与∠AFC的数量关系，并说明理由.

    查看试题解析

  • 12. 如图，在△ABC中，AD平分∠BAC，CE⊥AD于点G，交AB于点E，EF∥BC交AC于点F，交AD于H.

    (1)、求证：∠DEC=∠FEC；
    (2)、求证：EF=DC+HF.

    查看试题解析

  • 13. 如图，△ABC和△ADE关于直线MN对称，BC与DE的交点F在直线MN上. 

     

    (1)、若∠BAC＝100°，∠CAD＝30°，求∠EAF的度数. 
    (2)、若BC∥AD，AE平分∠BAM，∠BFE+∠C＝81°，求∠EAF的度数. 

    查看试题解析

  • 14. 如图，在平行四边形ABCD中，过点D作DE⊥AB于点E，点F在边CD上，且FC=AE ， 连接AF、BF．

    (1)、求证：四边形DEBF是矩形；
    (2)、若AF平分∠DAB，FC=6 ， DF=10 ， 求BF的长．

    查看试题解析

  • 15. 已知：如图，点C在∠MON的一边OM上，过点C的直线AB//ON ， CD平分∠ACM ， CE⊥CD.

    (1)、若∠O=50° ， 求∠BCD的度数； 
    (2)、求证：CE平分∠OCA； 
    (3)、当∠O为多少度时，CA分∠OCD成1：2两部分，并说明理由.

    查看试题解析

  • 16. 如图

    (1)、如图1，在▱ABCD中，AE平分∠BAD交CD边于点E，已知AB=5cm，AD=3cm，则EC等于cm。
    (2)、如图2，在▱ABCD中，若AE，BE分别是∠DAB，∠CBA的平分线，点E在DC边上，且AB=4，则▱ABCD的周长为。
    (3)、如图3，已知四边形ABCD是平行四边形，AD=BC，若AF，BE分别是∠DAB，∠CBA的平分线。求证：DF=EC
    (4)、在（3）的条件下，如果AD=3，AB=5，则EF的长为。

    查看试题解析

  • 17. 如图1，点A、B分别在射线OM、ON上运动（不与点O重合），AC、BC分别是∠BAO和∠ABO的角平分线，BC延长线交OM于点G．

    (1)、若∠MON=60°，则∠ACG= ；（直接写出答案）
    (2)、若∠MON=n°，求出∠ACG的度数；（用含n的代数式表示）
    (3)、如图2，若∠MON=80°，过点C作CF∥OA交AB于点F，求∠BGO与∠ACF的数量关系．

    查看试题解析

  • 18. 问题情境

    在综合与实践课上，同学们以“一个含30°的直角三角尺和两条平行线”为背景开展数学活动如图1，已知两直线a，b且a∥b和直角三角形ABC ， ∠BCA=90° ， ∠BAC=30° ， ∠ABC=60°.

    (1)、在图1中，∠1=46° ， 求∠2的度数；
    (2)、如图2，创新小组的同学把直线a向上平移，并把∠2的位置改变，发现∠2−∠1是一个定值，请写出这个定值，并说明理由；

    (3)、缜密小组在创新小组发现结论的基础上，将图2中的图形继续变化得到图3，AC平分∠BAM ， 此时发现∠1与∠2又存在新的数量关系，请直接写出∠1与∠2的数量关系.

    查看试题解析

四、第二十题突破

  • 19. 如图1，AB∥CD ， 点E，F分别在直线CD，AB上，∠BEC＝2∠BEF，过点A作AG⊥BE的延长线交于点G，交CD于点N，AK平分∠BAG，交EF于点H，交BE于点M．

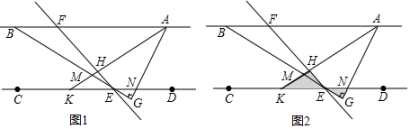    (1)、直接写出∠AHE，∠FAH，∠KEH之间的关系： ．
    (2)、若∠BEF=12∠BAK ， 求∠AHE．
    (3)、如图2，在（2）的条件下，将△KHE绕着点E以每秒5°的速度逆时针旋转，旋转时间为t，当KE边与射线ED重合时停止，则在旋转过程中，当△KHE的其中一边与△ENG的某一边平行时，直接写出此时t的值.

    查看试题解析

  • 20. 如图1，在Rt△ABC中，∠C=90° ， AC=8 ， BC=6 ， BD平分△ABC的外角∠ABM ， AD⊥BD于点D，过B点作BE∥AC交AD于点E.点P在线段AB上（不与端点A点重合），点Q在射线BC上，且CQ=2AP=2t ， 连接 PQ，作P点关于直线BE的对称点N，连接PN，NQ.

    (1)、求证：∠BAD=∠DBE.
    (2)、当Q在线段BC上时，PN与AD交于点H，若AH=EH ， 求HP的长.
    (3)、①当△PNQ的一边与△ABD的AD或BD边平行时，求所有满足条件的t的值.

    ②当点D在△PNQ内部时，请直接写出满足条件的t的取值范围.

    查看试题解析

  • 21. 已知：直线AB、CR被直线UV所截，直线UV交直线AB于点B，交直线CR于点D，∠ABU+∠CDV＝180°．

    (1)、如图1，求证：AB∥CD；
    (2)、如图2，BE∥DF，∠MEB＝∠ABE+5°，∠FDR＝35°，求∠MEB的度数；
    (3)、如图3，在（2）的条件下，点N在直线AB上，分别连接EN、ED，MG∥EN，连接ME，∠GME＝∠GEM，∠EBD＝2∠NEG，EB平分∠DEN，MH⊥UV于点H，若∠EDC＝17∠CDB，求∠GMH的度数．

    查看试题解析

  • 22. 已知直线AB∥CD，P为平面内一点，连接PA、PD．

    (1)、如图1，已知∠A＝50°，∠D＝150°，求∠APD的度数；
    (2)、如图2，判断∠PAB、∠CDP、∠APD之间的数量关系为  ．
    (3)、如图3，在（2）的条件下，AP⊥PD，DN平分∠PDC，若∠PAN+12∠PAB＝∠APD，求∠AND的度数．

    查看试题解析