备考2023年中考数学温州卷变式阶梯训练:第17-19题
试卷更新日期:2023-04-15 类型:三轮冲刺
一、第十七题
-
1.(1)、计算: .(2)、解不等式 ,并把解表示在数轴上.
 2.(1)、计算: .(2)、解不等式 ,并把解集表示在数轴上
2.(1)、计算: .(2)、解不等式 ,并把解集表示在数轴上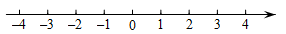 3.(1)、计算;(2)、解不等式组 , 并将解集表示在数轴上.
3.(1)、计算;(2)、解不等式组 , 并将解集表示在数轴上. 4.(1)、;(2)、解不等式 , 并把解集表示在数轴.5.(1)、计算:(2)、解不等式 , 并在数轴上表示解集.
4.(1)、;(2)、解不等式 , 并把解集表示在数轴.5.(1)、计算:(2)、解不等式 , 并在数轴上表示解集. 6. (1)计算: ﹣(π﹣1)0﹣4sin45°;
6. (1)计算: ﹣(π﹣1)0﹣4sin45°;(2)解不等式x> x﹣2,并将其解集表示在数轴上.
 7.(1)、(2)、解不等式 ,并把它的解集在数轴上表示出来.
7.(1)、(2)、解不等式 ,并把它的解集在数轴上表示出来.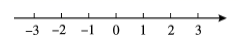 (3)、解方程组:(4)、解不等式组:8. 计算:(1)、;(2)、;(3)、;(4)、.9.(1)、计算: .(2)、解不等式组:10. 计算:.11. 计算下列各题:(1)、;(2)、;(3)、.12. 解下列不等式(组),并把解集在数轴上表示出来.(1)、解不等式:.(2)、解不等式组:.13.(1)、解方程组:(2)、解不等式: ,并把解集在数轴上表示出来,同时写出它的最大整数解.
(3)、解方程组:(4)、解不等式组:8. 计算:(1)、;(2)、;(3)、;(4)、.9.(1)、计算: .(2)、解不等式组:10. 计算:.11. 计算下列各题:(1)、;(2)、;(3)、.12. 解下列不等式(组),并把解集在数轴上表示出来.(1)、解不等式:.(2)、解不等式组:.13.(1)、解方程组:(2)、解不等式: ,并把解集在数轴上表示出来,同时写出它的最大整数解.二、第十八题
-
14. 如图,在 2×6 的方格纸中,已知格点P,请按要求画格点图形(顶点均在格点上).
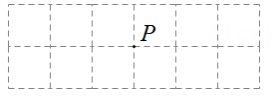
注:图1,图2在答题纸上.
(1)、在图1中画一个锐角三角形,使P为其中一边的中点,再画出该三角形向右平移2个单位后的图形.(2)、在图2中画一个以P为一个顶点的钝角三角形,使三边长都不相等,再画出该三角形绕点P旋转 180° 后的图形.15. 如图,在由边长为1个单位长度的小正方形组成的网格中,的顶点均为格点(网格线的交点).
( 1 )以A为旋转中心,将逆时针旋转 , 得到 , 请画出
( 2 )将向上平移7个单位长度,再向左平移2个单位长度,得到 , 请画出
16. 如图,在正方形网格中,△ABC的三个顶点都在格点上,结合所给的平面直角坐标系解答下列问题:
( 1 )将△ABC向右平移5个单位长度,画出平移后的△A1B1C1 ;
( 2 )画出△ABC关于x轴对称的△A2B2C2 ;
( 3 )将△ABC绕原点O 旋转180°,画出旋转后的△A3B3C3 ;
17. 在平面直角坐标系中,的位置如图所示,其中 , , . (1)、将向左平移6个单位长度,点 , , 的对应点分别为点 , , , 画出平移后得到的;(2)、将绕着点顺时针旋转90°,点 , , 的对应点分别为点 , , , 画出旋转后得到的 , 并直接写出点 , , 的坐标.18. 如图是由边长为 的小正方形构成的网格.每个小正方形的顶点叫做格点. 的顶点在格点上,仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题:
(1)、将向左平移6个单位长度,点 , , 的对应点分别为点 , , , 画出平移后得到的;(2)、将绕着点顺时针旋转90°,点 , , 的对应点分别为点 , , , 画出旋转后得到的 , 并直接写出点 , , 的坐标.18. 如图是由边长为 的小正方形构成的网格.每个小正方形的顶点叫做格点. 的顶点在格点上,仅用无刻度的直尺在给定网格中画图,画图过程用虚线表示,画图结果用实线表示,按步骤完成下列问题: (1)、将边 绕点 逆时针旋转 得到线段 ;(2)、画 的高 ;(3)、将点 竖直向下平移 个单位长度得到点 ,画出点 ;(4)、画线段 关于直线 的对称线段 .19. 如图,在 方格纸中,点 , 都在格点上 两条网格线的交点叫格点 ,用无刻度的直尺完成以下作图.
(1)、将边 绕点 逆时针旋转 得到线段 ;(2)、画 的高 ;(3)、将点 竖直向下平移 个单位长度得到点 ,画出点 ;(4)、画线段 关于直线 的对称线段 .19. 如图,在 方格纸中,点 , 都在格点上 两条网格线的交点叫格点 ,用无刻度的直尺完成以下作图.
⑴将线段 向上平移两个单位长度,点 的对应点为 ,点 的对应点为 ,请画出平移后的线段 ;
⑵将线段 绕点 按逆时针方向旋转 ,点 的对应点为点 ,请画出旋转后的线段 ;
⑶连结 , ,作 的边 上的高,若方格纸中小正方形的边长为1,求这条高线的长.
20. 线段在平面直角坐标系中的位置如图7所示,其中每个小正方形的边长为1个单位长度.
⑴将线段向左平移6个单位长度,作出平移后的线段;
⑵再将线段绕点顺时针旋转180°后得到线段;
⑶观察线段和线段 , 它们是否关于某点成中心对称?若是,请写出对称中心的坐标.
21. 如图,正方形网格中,每个小正方形的边长都是1个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,2),B(5,5),C(1,1)均在格点上.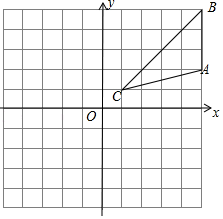
⑴将△ABC向下平移5个单位长度得到△A1B1C1 , 画出△A1B1C1;
⑵画出△A1B1C1绕点C1逆时针旋转90°后得到的△A2B2C1;
⑶在(2)的条件下,求△A1B1C1扫过的面积.
22. 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(1,3),B(2,5),C(4,2)(每个方格的边长均为1个单位长度)
⑴将△ABC平移,使点A移动到点A1 , 请画出△A1B1C1;
⑵作出△ABC关于O点成中心对称的△A2B2C2 , 并直接写出A2 , B2 , C2的坐标;⑶△A1B1C1与△A2B2C2是否成中心对称?若是,请写出对称中心的坐标;若不是,请说明理由.
23. 如图,方格中每个小正方形的边长为1个单位长度,的顶点和线段的端点均在小正方形的顶点上. (1)、在方格纸中将向下平移3个单位长度,再向左平移2个单位长度后得到(点的对应点是点 , 点的对应点是 , 点的对应点是点),请画出;(2)、在(1)画出后,在方格纸中画出(点在小正方形的顶点上),使 , 的面积为15,连接 , 请直接写出的长.24. (2016黑龙江省龙东地区)如图,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)(﹣2,1),先将△ABC沿一确定方向平移得到△A1B1C1 , 点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2 , 点A1的对应点为点A2 .
(1)、在方格纸中将向下平移3个单位长度,再向左平移2个单位长度后得到(点的对应点是点 , 点的对应点是 , 点的对应点是点),请画出;(2)、在(1)画出后,在方格纸中画出(点在小正方形的顶点上),使 , 的面积为15,连接 , 请直接写出的长.24. (2016黑龙江省龙东地区)如图,在平面直角坐标系中,点A、B、C的坐标分别为(﹣1,3)、(﹣4,1)(﹣2,1),先将△ABC沿一确定方向平移得到△A1B1C1 , 点B的对应点B1的坐标是(1,2),再将△A1B1C1绕原点O顺时针旋转90°得到△A2B2C2 , 点A1的对应点为点A2 .
( 1 )画出△A1B1C1;
( 2 )画出△A2B2C2;
( 3 )求出在这两次变换过程中,点A经过点A1到达A2的路径总长.
25. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(﹣3,2),B(0,4),C(0,2).
( 1 )将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(1,﹣4),画出平移后对应的△A2B2C2;
( 2 )若将△A1B1C绕某一点旋转可以得到△A2B2C2;请直接写出旋转中心的坐标;
( 3 )在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.
三、第十九题
-
26. 为了解某校400名学生在校午餐所需的时间,抽查了20名学生在校午餐所花的时间,由图示分组信息得:A,C,B,B,C,C,C,A,B,C,C,C,D,B,C,C,C,E,C,C.
分组信息
A组:
B组:
C组:
D组:
E组:
注:x(分钟)为午餐时间!
某校被抽查的20名学生在校午餐所花时间的频数表
组别
划记
频数
A

2
B

4
C
▲
▲
D
▲
▲
E
▲
▲
合计
20
(1)、请填写频数表,并估计这400名学生午餐所花时间在C组的人数.(2)、在既考虑学生午餐用时需求,又考虑食堂运行效率的情况下,校方准备在15分钟,20分钟,25分钟,30分钟中选择一个作为午餐时间,你认为应选择几分钟为宜?说明理由.27. 2022年末,中国迎来第一波疫情高峰.为加强同学们的防护意识,某校举行了以“疫情防护”为主题的知识竞赛活动.发现该校全体学生的竞赛成绩(百分制)均不低于60分,现从中随机抽取n名学生的竞赛成绩进行整理和分析(成绩得分用x表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图,下面为部分数据:其中“”这组的部分数据(从小到大排序)如下:80,82,82,83,83,84,85,85,85,86,87,87,87,88,88……其中“”这组的数据如下:90,92,93,95,95,96,96,96,97,100.竞赛成绩分组统计表
组别
竞赛成绩分组
频数
平均分
1
8
65
2
a
75
3
b
88
4
10
95

根据以上信息,回答下列问题:
(1)、下列说法正确的是____.A、样本为n名学生 B、a=12 C、m=40(2)、“”这组的数据的众数是 .(3)、随机抽取的这n名学生竞赛成绩的中位数是;平均分是;(4)、若学生竞赛成绩达到96分以上(含96分)获奖,请你估计全校1200名学生中获奖的人数.28. 第24届冬奥会于今年2月份在我国北京市和张家口市顺利举行,这是中国历史上第一次举办冬季奥运会.随着冬奥会的成功举办,冰雪运动在全国各地也得到了进一步音及和发展.依托这一良好契机,我省某中学组织了以“走入冰雪,享受快乐”为主题的冰雪知识竞赛,并随机抽取了部分学生的竞赛成绩(百分制)进行整理和分析(将分数分为四组:A. , B. , C. , D.),下面给出了部分信息:

抽取的学生竞赛成绩分布表
级别
分数/分
频数
A
a
B
12
C
6
D
3
请解答下列问题:
(1)、直接写出a的值是、B所占的百分比是;(2)、该校共有300名学生参加了此次冰雪知识竞赛活动,估计在本次活动中取得分数在80分及以上的有多少人?(3)、学校计划从在本次竞赛中获得高分的小明,小亮,小颖和小白四名同学中随机选择两名同学作为宣传讲解员,为同学们科普冰雪运动的相关知识,请你用树状图或列表的方法求出小明和小颖被同时选中的概率.29. 在体育活动课中,体育老师随机抽取了九年级甲、乙两班部分学生进行某体育项目的测试,并对成绩进行统计分析,绘制了频数分布表,请你根据表中的信息完成下列问题:分 组
频数
频率
第一组(不及格)
3
0.15
第二组(中)
b
0.20
第三组(良)
7
0.35
第四组(优)
6
a
(1)、频数分布表中 , ;(2)、如果该校九年级共有学生900人,估计该校该体育项目的成绩为良和优的学生有多少人?(3)、已知第一组中有两个甲班学生,第二组中只有一个乙班学生,老师随机从这两个组中各选一名学生对体育活动课提出建议,则所选两人正好是甲班和乙班各一人的概率是多少?30. 某校要加强中小学生作业、睡眠、手机、读物、体质管理.数学社团成员采用随机抽样的方法,抽取了七年级若干名学生,对他们一周内平均每天的睡眠时间t(单位:h)进行了调查,将数据整理后得到下列不完整的统计表和扇形统计图.请根据图表信息解答下列问题. (1)、本次被抽取的七年级学生共有名,统计表中,m=(2)、扇形统计图中,C组所在扇形的圆心角的度数是度;(3)、请估计该校800名七年级学生中睡眠不足7小时的人数.
(1)、本次被抽取的七年级学生共有名,统计表中,m=(2)、扇形统计图中,C组所在扇形的圆心角的度数是度;(3)、请估计该校800名七年级学生中睡眠不足7小时的人数.组别
睡眠时间分组
频数
A
t<6
4
B
6≤t<7
8
C
7≤t<8
10
D
8≤t<9
21
E
t≥9
m
31. 为了解同学们每月零花钱数额,校园小记者随机调查了本校部分学生,并根据调查结果绘制出如下不完整的统计图表:学生每月零花线频数分布表:
零花钱数额x/元
人数(频数)
频率
6
0.15
12
0.30
16
0.40
b
0.10
2
a
学生每月零花钱频数直方图:
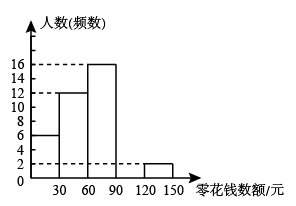
请根据以上图表,解答下列问题:
(1)、这次被调查的人数共有人, , ;(2)、计算并补全频数分布直方图;(3)、请估计该校1500名学生中每月零花钱数额低于90元的人数.32. 为实现全员脱贫目标,某村贫困户在当地政府支持帮助下,办起了养鸡场.经过一段时间精心饲养,总量为3000只的一批鸡可以出售.现从中随机抽取50只,得到它们质量的统计数据如下表:组别
质量/千克
频数(只)
A
6
B
a
C
14
D
9
根据以上信息,解答下列问题:
(1)、表中a=.(2)、这50只鸡质量的中位数落在组.(3)、估计这3000只鸡中质量不小于1.7千克的有多少只?(4)、这些贫困户的总收入达到68000元就能实现全员脱贫目标.若这50只鸡的总质量为80千克,按每千克15元的市场价格来销售这批鸡,通过计算说明该村贫困户能否脱贫.33. 近年来,随着社会的发展,学校,家庭等社会问题的日益复杂化,心理健康教育已成为学校教育的一个新课题.某中学开设了“家校心理疏导”课程,为了解学生的前置情况,学生处对全校学生进行了问卷测评,从中随机抽取了50份问卷,统计成绩,并将结果绘制出不完整的频数分布表和频数分布直方图如图表:组别
成绩x(分)
频数(人数)
合组总分(分)
第1组
4
220
第2组
8
520
第3组
16
1200
第4组
a
1020
第5组
10
950

根据以上信息,回答下列问题:
(1)、a= , 并补全频数分布直方图;(2)、本次所抽取的学生测评成绩的中位数位于哪个组?并求本次所抽取的学生测评成绩的平均数;(3)、若测评成绩不低于80分为优秀,试估计该校2000名学生测评成绩为优秀的人数是多少?34. 为庆祝中国共产党建党100周年,某校开展了党史知识竞赛.某年级随机选出了一个班的初赛成绩进行统计,得到如下统计图表,已知在扇形统计图分数段对应的扇形六圆心角为 . 某校组织读书征文比赛活动,评选出一、二、三等奖若干名,并绘成如图所示的统计表和扇形统计图(不完整),请你根据图中信息解答下列问题:统计表
分段
成绩范围(分)
频数
频率
90~100
0.1
80~89
20
70~79
0.3
70分以下
10
注:90~100表示成绩 , 满足 , 以下相同.
扇形统计图
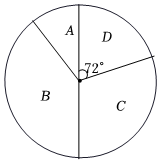 (1)、在统计表中, , , ;(2)、若该年级参加初赛的学生共有2000人,根据以上统计数据估计该年级成绩在90分及以上的学生人数;(3)、若统计表分数段的男生比女生少1人,从段中任选2人参加复赛,请用列表法或画树状图的方法,求出恰好抽到1名男生和1名女生的概率.35. 为倡导绿色健康节约的生活方式,某社区开展“垃圾分类,从我做起”的活动,志愿者随机抽取了社区内50名居民,对其3月份垃圾分类投放次数进行了调查,并对数据进行了统计整理,以下是部分数据和不完整的统计图表:
(1)、在统计表中, , , ;(2)、若该年级参加初赛的学生共有2000人,根据以上统计数据估计该年级成绩在90分及以上的学生人数;(3)、若统计表分数段的男生比女生少1人,从段中任选2人参加复赛,请用列表法或画树状图的方法,求出恰好抽到1名男生和1名女生的概率.35. 为倡导绿色健康节约的生活方式,某社区开展“垃圾分类,从我做起”的活动,志愿者随机抽取了社区内50名居民,对其3月份垃圾分类投放次数进行了调查,并对数据进行了统计整理,以下是部分数据和不完整的统计图表:信息1:垃圾分类投放次数分布表信息
组别
投放次数
频数
A
a
B
10
C
c
D
14
E
e
合计
50

信息3:C组包含的数据:12,12,10,12,13,10,11,13,12,11,13.
请结合以上信息完成下列问题:
(1)、统计表中的a= , e=;(2)、统计图中B组对应扇形的圆心角为度;(3)、C组数据的众数是 , 抽取的50名居民3月份垃圾分类投放次数的中位数是;(4)、根据调查结果,请你估计该社区2000名居民中3月份垃圾分类投放次数不少于15次的人数.36. 为落实教育部“双减”政策,某市从2021年9月起,各中小学全面开展课后延时服务.为了了解该市甲、乙两所中学延时服务的情况,在这两所学校分别随机抽查了100名家长进行问卷调查.家长对延时服务的综合评分记为x,将所得数据分为5个等级(A“很满意”:;B“满意”:;“比较满意”:;D“不太满意”:;E“不满意”:),将数据进行整理后,得到如下统计图和统计表.①甲中学延时服务得分的扇形统计图
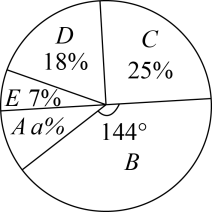
②乙中学延时服务得分频数分布统计表
等级
满意度
得分
频数
A
很满意
15
B
满意
C
比较满意
30
D
不太满意
10
E
不满意
5
③甲、乙两中学延时服务得分的平均数、中位数、众数如下表:
学校
平均数
中位数
众数
甲
78
79.5
80
乙
80
85
④乙中学的等级“B”的分数从高到低排列,排在最后的10个数据分别是:84,84,83,83,83,81,80,80,80,80.
请你根据以上信息,回答下列问题:
(1)、直接写出a和b的值;(2)、课后延时服务综合得分在70分及以上为合格,请你估计甲中学3000名家长中认为该校课后延时服务合格的人数;(3)、小明说:“乙中学的课后延时服务比甲中学好”,你同意小明的说法吗?请写出一条理由.