备考2023年中考数学温州卷变式阶梯训练:第14-16题
试卷更新日期:2023-04-15 类型:三轮冲刺
一、第十四题
-
1. 若扇形的圆心角为 120° ,半径为 ,则它的弧长为 .2. 已知一个扇形的圆心角为 , 面积为 , 则此扇形的弧长为.3. 一个扇形的圆心角为 , 弧长为 , 则此扇形的半径是.4. 在半径为1的圆中,圆心角所对的弧长是.5. 若扇形的弧长为 , 圆心角为 , 则该扇形的半径为.6. 如图,点A在半圆O上,BC为直径.若∠ABC=30°,BC=3,则的长是 .
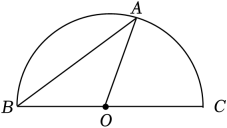 7. 如图,点A在半圆O上,BC为直径,若=120°,BC=6,则的长是 .
7. 如图,点A在半圆O上,BC为直径,若=120°,BC=6,则的长是 . 8. 如图,点 , , , 在半径为的上,连接 , , , . 若 , 则劣弧的长为 .
8. 如图,点 , , , 在半径为的上,连接 , , , . 若 , 则劣弧的长为 .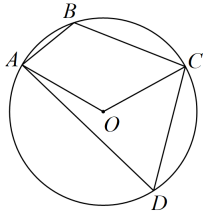 9. 如图,四边形内接于 , , , , 则劣弧的长度为 .
9. 如图,四边形内接于 , , , , 则劣弧的长度为 . 10. 如图,AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q. 若AB=4,则弧BQ的长为.
10. 如图,AB为半圆O的直径,现将一块等腰直角三角板如图放置,锐角顶点P在半圆上,斜边过点B,一条直角边交该半圆于点Q. 若AB=4,则弧BQ的长为. 11. 新定义:在中,点D、E分别是边的中点,如果上的所有点都在的内部或边上,那么称为的中内弧.已知在中, , , 点D、E分别是边的中点,如果是的中内弧,那么长度的最大值等于 .12. 如图,将矩形绕其右下角的顶点按顺时针方向旋转至图①位置,继续绕右下角的顶点按顺时针方向旋转至图②位置,以此类推,这样连续旋转2022次.若 , 则顶点A在整个旋转过程中所经过的路径总长为 .
11. 新定义:在中,点D、E分别是边的中点,如果上的所有点都在的内部或边上,那么称为的中内弧.已知在中, , , 点D、E分别是边的中点,如果是的中内弧,那么长度的最大值等于 .12. 如图,将矩形绕其右下角的顶点按顺时针方向旋转至图①位置,继续绕右下角的顶点按顺时针方向旋转至图②位置,以此类推,这样连续旋转2022次.若 , 则顶点A在整个旋转过程中所经过的路径总长为 .
二、第十五题
-
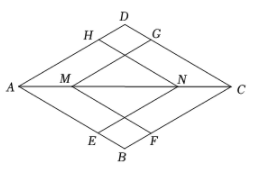
13. 如图,在菱形ABCD中, AB=1,∠BAD=60°.在其内部作形状、大小都相同的菱形 AENH 和菱形 CGMF ,使点E,F,G,H分别在边 AB、BC、CD、DA 上,点M,N在对角线 AC 上.若 AE=3BE,则 MN 的长为 .
 14. 如图,菱形 中,分别以点 、 为圆心,大于 长为半径作弧,两弧分别交于点 、 ,作直线 ,且直线 恰好经过点 ,与边 交于点 .连接 ,若 ,则 .
14. 如图,菱形 中,分别以点 、 为圆心,大于 长为半径作弧,两弧分别交于点 、 ,作直线 ,且直线 恰好经过点 ,与边 交于点 .连接 ,若 ,则 . 15. 如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为 .
15. 如图,已知菱形ABCD的边长为2,∠BAD=60°,若DE⊥AB,垂足为点E,则DE的长为 . 16. 如图,在菱形ABCD中,AB=AC=10,对角线AC、BD相交于点O , 点M在线段AC上,且AM=3,点P为线段BD上的一个动点,则MP+ PB的最小值是 .
16. 如图,在菱形ABCD中,AB=AC=10,对角线AC、BD相交于点O , 点M在线段AC上,且AM=3,点P为线段BD上的一个动点,则MP+ PB的最小值是 . 17. 如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为.
17. 如图,在菱形ABCD中,AB=4,∠A=120°,点P,Q,K分别为线段BC,CD,BD上的任意一点,则PK+QK的最小值为.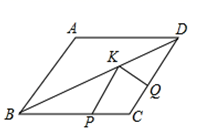 18. 在菱形ABCD中,AB=4,∠ABC=60°,连接AC,BD,E是菱形边上或对角线上一点,且∠CAE=30°,则BE的长为 .19. 如图,边长为2的菱形 的顶点 , 分别在直角 的边 , 上滑动.若 ,则线段 的最大值为.
18. 在菱形ABCD中,AB=4,∠ABC=60°,连接AC,BD,E是菱形边上或对角线上一点,且∠CAE=30°,则BE的长为 .19. 如图,边长为2的菱形 的顶点 , 分别在直角 的边 , 上滑动.若 ,则线段 的最大值为. 20. 如图,在菱形ABCD中,tanA= ,M , N分别在AD , BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D , 当EF⊥AD时, 的值为 .
20. 如图,在菱形ABCD中,tanA= ,M , N分别在AD , BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D , 当EF⊥AD时, 的值为 . 21. 如图,菱形 中, ,点 在 边上,且 ,动点 在 边上,连接 ,将线段 绕点 顺时针旋转 至线段 ,连接 ,则线段 长的最小值为 .
21. 如图,菱形 中, ,点 在 边上,且 ,动点 在 边上,连接 ,将线段 绕点 顺时针旋转 至线段 ,连接 ,则线段 长的最小值为 . 22. 如图,在边长为6的菱形 中, 为其对角线, ,点 、 分别是边 、 上的动点,且 .连接 、 、 , 交 于点 .则点 到直线 的距离的最大值为.
22. 如图,在边长为6的菱形 中, 为其对角线, ,点 、 分别是边 、 上的动点,且 .连接 、 、 , 交 于点 .则点 到直线 的距离的最大值为.
三、第十六题
-
23. 如图是某风车示意图,其相同的四个叶片均匀分布,水平地而上的点M在旋转中心O的正下方。某一时刻,太阳光线恰好垂直照射叶片 OA、OB ,此时各叶片影子在点M右侧成线段 CD ,测得MC=8.5m,CD=13m,垂直于地面的木棒 EF 与影子 FG 的比为2∶3,则点O,M之间的距离等于米.转动时,叶片外端离地面的最大高度等于米.
 24. 小明和小杰去公园游玩,小明给站在观景台边缘的小杰拍照时,发现他的眼睛、凉亭顶端、小杰的头顶三点恰好在一条直线上(如图所示).已知小明的眼睛离地面的距离为米,凉亭的高度为米,小明到凉亭的距离为米,凉亭与观景台底部的距离为米,小杰身高为米.那么观景台的高度为米.
24. 小明和小杰去公园游玩,小明给站在观景台边缘的小杰拍照时,发现他的眼睛、凉亭顶端、小杰的头顶三点恰好在一条直线上(如图所示).已知小明的眼睛离地面的距离为米,凉亭的高度为米,小明到凉亭的距离为米,凉亭与观景台底部的距离为米,小杰身高为米.那么观景台的高度为米. 25. 如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD= 米,则路灯的灯柱BC高度应该设计为米(计算结果保留根号).
25. 如图,要在宽AB为20米的瓯海大道两边安装路灯,路灯的灯臂CD与灯柱BC成120°角,灯罩的轴线DO与灯臂CD垂直,当灯罩的轴线DO通过公路路面的中心线(即O为AB的中点)时照明效果最佳,若CD= 米,则路灯的灯柱BC高度应该设计为米(计算结果保留根号).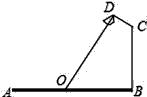 26. 如图,树在路灯O的照射下形成投影 , 已知路灯高 , 树影 , 树与路灯O的水平距离 , 则树的高度长是.
26. 如图,树在路灯O的照射下形成投影 , 已知路灯高 , 树影 , 树与路灯O的水平距离 , 则树的高度长是.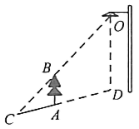 27. 如图所示,某校数学兴趣小组利用自制的直角三角形硬纸板来测量操场旗杆的高度,他们通过调整测量位置,使斜边与地面保持平行,并使边与旗杆顶点在同一直线上,已知米,米,目测点到地面的距离米,到旗杆水平的距离米,则旗杆的高度为米.
27. 如图所示,某校数学兴趣小组利用自制的直角三角形硬纸板来测量操场旗杆的高度,他们通过调整测量位置,使斜边与地面保持平行,并使边与旗杆顶点在同一直线上,已知米,米,目测点到地面的距离米,到旗杆水平的距离米,则旗杆的高度为米. 28. 如图是一位同学用激光笔测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙的顶端C处,若 , , 测得 , , , 则该古城墙的高度是.
28. 如图是一位同学用激光笔测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙的顶端C处,若 , , 测得 , , , 则该古城墙的高度是. 29. 如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,且Rt△ABC与△AEM在同一个平面内.已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为 米.
29. 如图,数学兴趣小组利用硬纸板自制的Rt△ABC来测量操场旗杆MN的高度,他们通过调整测量位置,并使边AC与旗杆顶点M在同一直线上,且Rt△ABC与△AEM在同一个平面内.已知AC=0.8米,BC=0.5米,目测点A到地面的距离AD=1.5米,到旗杆的水平距离AE=20米,则旗杆MN的高度为 米. 30. 如图是某路灯的示意图,立柱OE与水平地面垂直,两盏路灯挂在灯杆OE的异侧(灯臂AB,CD近似看作线段,AB、CD),AE⊥OE,∠ABO=∠DCO=120°.小丽(身高1.5米)站在点P处时,点F,D,E在同一直线上,向后移动4.5米到达点Q,点G,D,B,A在同一直线上.测得OP=6米,则OE=米,AB=米.
30. 如图是某路灯的示意图,立柱OE与水平地面垂直,两盏路灯挂在灯杆OE的异侧(灯臂AB,CD近似看作线段,AB、CD),AE⊥OE,∠ABO=∠DCO=120°.小丽(身高1.5米)站在点P处时,点F,D,E在同一直线上,向后移动4.5米到达点Q,点G,D,B,A在同一直线上.测得OP=6米,则OE=米,AB=米. 31. 如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上。在F点观测A点后,沿FN方向走到M点.观测C点发现∠1=∠2。测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为米,BC为米。
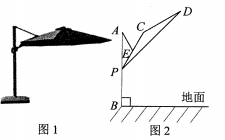
31. 如图,在河对岸有一矩形场地ABCD,为了估测场地大小,在笔直的河岸l上依次取点E,F,N,使AE⊥l,BF⊥l,点N,A,B在同一直线上。在F点观测A点后,沿FN方向走到M点.观测C点发现∠1=∠2。测得EF=15米,FM=2米,MN=8米,∠ANE=45°,则场地的边AB为米,BC为米。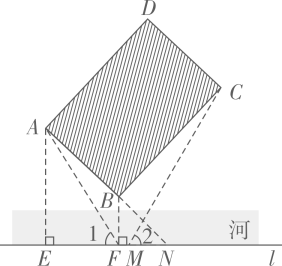 32. 某户外遮阳棚如图1,其截面结构示意图如图2所示.支撑柱AB上地面,AB=120 cm,Р是支撑柱AB上一动点,伞杆CP可绕着中点E旋转,CD=CP=40 cm,斜拉杆AE可绕点A旋转,AE= CP.若∠APE=30°,则BP=cm;伞展开长 PD==300cm,若A,C,D在同一条直线上,某时太阳光线恰好与地面垂直,则PD落到地面的阴影长为cm.
32. 某户外遮阳棚如图1,其截面结构示意图如图2所示.支撑柱AB上地面,AB=120 cm,Р是支撑柱AB上一动点,伞杆CP可绕着中点E旋转,CD=CP=40 cm,斜拉杆AE可绕点A旋转,AE= CP.若∠APE=30°,则BP=cm;伞展开长 PD==300cm,若A,C,D在同一条直线上,某时太阳光线恰好与地面垂直,则PD落到地面的阴影长为cm.