备考2023年中考数学温州卷变式阶梯训练：第11-13题

试卷更新日期：2023-04-15 类型：三轮冲刺

进入出卷网下载

一、第十一题

1. 分解因式：m²-n²= ．

查看试题解析
2. 分解因式： $x^{2} - 25 =$ ．

查看试题解析
3. 因式分解 $y^{2} - 4 x^{2}$ 的结果是．

查看试题解析
4. 因式分解：b²﹣4b+4＝．

查看试题解析
5. 分解因式：a⁴﹣3a²﹣4＝.

查看试题解析
6. 因式分解： ${(m + n)}^{2} - 4 m^{2} =$ .

查看试题解析
7. 因式分解： $m (m + 8) + 9 - 2 m =$ ．

查看试题解析
8. 因式分解： ${(m + n)}^{2} - 6 (m + n) + 9 =$ ．

查看试题解析
9. 分解因式： $(x + y - 2 xy) (x + y - 2) + {(xy - 1)}^{2} =$ ．

查看试题解析
10. 在生活中很多场合都需要密码，有一种用因式分解法产生的密码，其原理是：如对于多项式 $a^{2} - b^{2}$ ，因式分解的结果是（a＋b）（a-b），若取a＝8，b＝3则各个因式的值是：（a＋b）＝11，（a-b）＝5，于是就可以把1105作为一个四位数的密码，那么对于多项式 $4 x^{2} - 9 y^{2}$ ，若取x＝4，y＝2时，用上述方法产生的四位数密码是．（写出一个即可）．

查看试题解析

二、第十二题

11. 某校5个小组在一次拉树活动中植树株数的统计图如图所示，则平均每组植树株．

查看试题解析
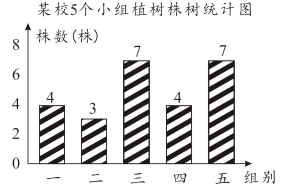12. 小明所在班级为希望工程捐款，他统计了全班同学的捐款情况，并绘制成如图所示的统计图，根据统计图，可计算出全班同学平均每人捐款元．

查看试题解析
13. 学校进行广播操比赛，如图是20位评委给某班的评分情况统计图，则该班的平均得分是分.

查看试题解析
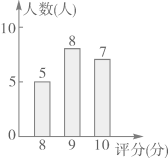14. 对一种环保电动汽车性能抽测，获得如下条形统计图.根据统计图可估计得被抽检电动汽车一次充电后平均里程数为.

查看试题解析
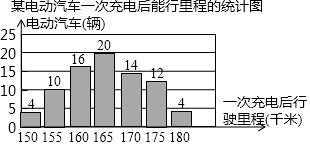15. 一次演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分．各项成绩均按百分制计，然后再按演讲内容占50%，演讲能力占40%、演讲效果占10%，计算选手的综合成绩（百分制）．进入决赛的前两名选手的单项成绩如表所示，则获得第一名的选手为．
选手
演讲内容
演讲能力
演讲效果
小明
90
80
90
小红
80
90
90

查看试题解析
16. 每年的4月23日是“世界读书日”，某校为了解4月份八年级学生的读书情况，随机调查了八年级50名学生读书的册数，数据整理如下：
册数
0
1
2
3
4
人数
9
3
20
15
3
由此估计该校八年级学生4月份人均读书册．

查看试题解析
17. 某校规定学生期末数学总评成绩由三部分构成：卷面成绩、课外论文成绩、平日表现成绩（三部分所占比例如图），若方方的三部分得分依次是92、80、84，则她这学期的期末数学总评成绩是．

查看试题解析
18. 某班体育委员统计了全班同学一周的体育锻炼时间（单位：小时），并绘制了如图所示的折线统计图，则该班同学的平均锻炼时间为.

查看试题解析
19. 每年五月第三个星期日是全国助残日.在今年助残日前夕，某班进行了公益捐款活动，小明对本班同学的捐款情况进行了统计，绘制成如图所示的不完整的统计图，其中捐100元的人数占全班总人数的10%，由统计图可得全班同学平均每人捐款元.

查看试题解析
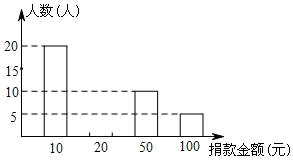20. 为了解某校学生的睡眠情况，该校数学小组随机调查了部分学生一周的平均每天睡眠时间，设每名学生的平均每天睡眠时间为x时，共分为四组：A.6≤x＜7，B.7≤x＜8，C.8≤x＜9，D.9≤x≤10，将调查结果绘制成如图两幅不完整的统计图．（注：学生的平均每天睡眠时间不低于6时且不高于10时．）若该校有1500名学生，根据抽样调查结果，请估计该校平均每天睡眠时间低于8时的学生有人．

查看试题解析

三、第十三题

21. 计算： $\frac{x^{2} + x y}{x y} + \frac{x y - x^{2}}{x y} =$ ．

查看试题解析
22. 化简 $\frac{x}{x - 3} + \frac{x - 6}{x - 3}$ ，结果等于．

查看试题解析
23. 化简： $\frac{4 x}{x^{2} - 4} - \frac{x}{x - 2} =$ .

查看试题解析
24. 计算 $\frac{2 a}{a - 1} - \frac{2}{a - 1}$ 的结果是.

查看试题解析
25. 计算 $\frac{1}{x - 1} - \frac{1}{x (x - 1)}$ 的结果为．

查看试题解析
26. 已知 $\frac{1}{x} - \frac{1}{y} = 6$ ，则分式 $\frac{x y}{x - y}$ 的值等于．

查看试题解析
27. 已知 $\frac{1}{x} - \frac{1}{y} = 2$ ，则代数式 $\frac{2 x + x y - 2 y}{x - x y - y}$ 的值是.

查看试题解析
28. 已知 $\frac{3 x - 4}{(x - 1) (x - 2)} = \frac{A}{x - 1} + \frac{B}{x - 2}$ ，则 $A + B =$ ．

查看试题解析
29. 已知 $xyz = 1$ ， $x + y + z = 2$ ， $x^{2} + y^{2} + z^{2} = 16.$ 则 $\frac{1}{xy + 2 z} + \frac{1}{yz + 2 x} + \frac{1}{zx + 2 y} =$ ．

查看试题解析
30. 设实a，b，c满足： $a + b + c = 3 ， a^{2} + b^{2} + c^{2} = 4$ ，则 $\frac{a^{2} + b^{2}}{2 - c} + \frac{b^{2} + c^{2}}{2 - a} + \frac{c^{2} + a^{2}}{2 - b}$ = ．

查看试题解析

选手	演讲内容	演讲能力	演讲效果
小明	90	80	90
小红	80	90	90

册数	0	1	2	3	4
人数	9	3	20	15	3