备考2023年中考数学温州卷变式阶梯训练:第6-10题
试卷更新日期:2023-04-15 类型:三轮冲刺
一、第六题
-
1. 若关于x的方程x2+6x+c=0有两个相等的实数根,则c的值是( )A、36 B、-36 C、9 D、-92. 关于x的一元二次方程有实数根,则a的取值范围是( )A、 B、 C、 D、3. 方程2x2-10=0的根的情况是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法确定;4. 关于的方程有两个相等的实数根,则( )A、 B、 C、 D、5. 若关于x的方程两根异号,则a的取值范围是( )A、 B、 C、 D、6. 有两个一元二次方程:M:ax2+bx+c=0,N:cx2+bx+a=0,以下四个结论中,错误的是( )A、如果方程M有两个不相等的实数根,那么方程N也有两个不相等的实数根 B、如果方程M有两根符号相同,那么方程N也有两根符号相同 C、如果5是方程M的一个根,那么 是方程N的一个根 D、如果方程M和方程N有一个相同的实数根,那么这个根必是x=17. 已知关于x的一元二次方程(其中p,q为常数)有两个相等的实数根,则下列结论中,错误的是( ).A、1可能是方程的根 B、可能是方程的根 C、0可能是方程的根 D、1和-1都是方程的根
二、第七题
-
8. 小聪某次从家出发去公园游玩的行程如图所示,他离家的路程为s米,所经过的时间为t分钟,下列选项中的图象,能近似刻画s与t之间关系的是( )
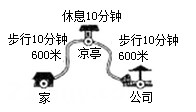 A、
A、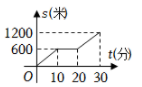 B、
B、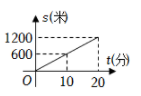 C、
C、 D、
D、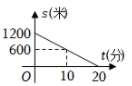 9. 一列火车由甲市驶往相距的乙市,火车的速度是时,火车离乙市的距离单位:随行驶时间单位:小时 变化的关系用图表示正确的是( )A、
9. 一列火车由甲市驶往相距的乙市,火车的速度是时,火车离乙市的距离单位:随行驶时间单位:小时 变化的关系用图表示正确的是( )A、 B、
B、 C、
C、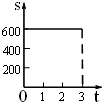 D、
D、 10. 如图,在长形中截取两个相同的圆作为圆柱的上、下底面,剩余的矩形作为圆柱的侧面,刚好能组合成圆住.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( )
10. 如图,在长形中截取两个相同的圆作为圆柱的上、下底面,剩余的矩形作为圆柱的侧面,刚好能组合成圆住.设矩形的长和宽分别为y和x,则y与x的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 11. 如图,和四边形DEFG分别是直角三角形和矩形, , cm,cm,于点B.若矩形DEFG从点B开始以每秒1cm的速度向右平移至点C,且矩形的边FG扫过的面积为S(),平移的时间为t(秒),则S与t之间的函数图象可能是( )
11. 如图,和四边形DEFG分别是直角三角形和矩形, , cm,cm,于点B.若矩形DEFG从点B开始以每秒1cm的速度向右平移至点C,且矩形的边FG扫过的面积为S(),平移的时间为t(秒),则S与t之间的函数图象可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 12. A、B两地相距240千米,慢车从A地到B地,快车从B地到A地,慢车的速度为120千米/小时,快车的速度为180千米/小时,两车同时出发.设两车的行驶时间为x(小时),两车之间的路程为y(千米).则能大致表示y与x之间函数关系的图象是( )A、
12. A、B两地相距240千米,慢车从A地到B地,快车从B地到A地,慢车的速度为120千米/小时,快车的速度为180千米/小时,两车同时出发.设两车的行驶时间为x(小时),两车之间的路程为y(千米).则能大致表示y与x之间函数关系的图象是( )A、 B、
B、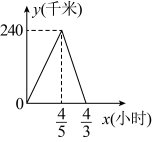 C、
C、 D、
D、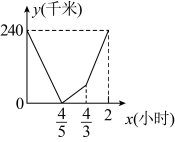 13. 周末小刚骑自行车到外婆家,他从家出发后到达书店,看了一会书,仍按原来的速度继续前行到达外婆家,小刚从家出发到外婆家中,小刚与家的距离随时间变化的函数图象大致如图所示,下列说法正确的是( )
13. 周末小刚骑自行车到外婆家,他从家出发后到达书店,看了一会书,仍按原来的速度继续前行到达外婆家,小刚从家出发到外婆家中,小刚与家的距离随时间变化的函数图象大致如图所示,下列说法正确的是( ) A、小刚从家到书店的骑行速度为5km/h B、小刚在书店停留了1.5h C、书店与外婆家的距离为15km D、小刚从家到外婆家的平均速度为6km/h14. 用表示a、b两数中较大的数,如 . 若函数y=max{1,(x>0)},则y与x之间的函数图象大致为( )A、
A、小刚从家到书店的骑行速度为5km/h B、小刚在书店停留了1.5h C、书店与外婆家的距离为15km D、小刚从家到外婆家的平均速度为6km/h14. 用表示a、b两数中较大的数,如 . 若函数y=max{1,(x>0)},则y与x之间的函数图象大致为( )A、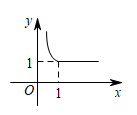 B、
B、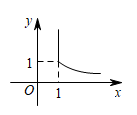 C、
C、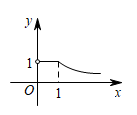 D、
D、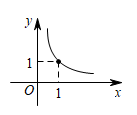 15. 如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2 , 运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )
15. 如图,△ABC为直角三角形,∠C=90°,BC=2cm,∠A=30°,四边形DEFG为矩形,DE=2cm,EF=6cm,且点C、B、E、F在同一条直线上,点B与点E重合.Rt△ABC以每秒1cm的速度沿矩形DEFG的边EF向右平移,当点C与点F重合时停止.设Rt△ABC与矩形DEFG的重叠部分的面积为ycm2 , 运动时间xs.能反映ycm2与xs之间函数关系的大致图象是( )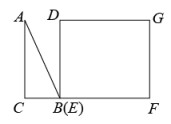 A、
A、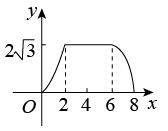 B、
B、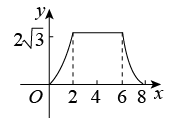 C、
C、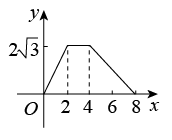 D、
D、
三、第八题
-
16. 如图, AB、AC是 ⊙O 的两条弦, OD⊥AB于点D, OE⊥AC 于点E,连结 OB、OC.若 ∠DOE=130° ,则 ∠BOC 的度数为( )
 A、95° B、100° C、105° D、130°17. 如图,AB是⊙O的直径,CD是⊙O的弦,连接AC,AD,BD.若∠CAB=36°,则∠ADC的度数为( )
A、95° B、100° C、105° D、130°17. 如图,AB是⊙O的直径,CD是⊙O的弦,连接AC,AD,BD.若∠CAB=36°,则∠ADC的度数为( ) A、72° B、54° C、45° D、36°18. 如图,四边形内接于 , , , 则( )
A、72° B、54° C、45° D、36°18. 如图,四边形内接于 , , , 则( )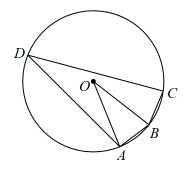 A、 B、 C、 D、无法确定19. 如图,AB是的弦,半径于点D, , 点P在圆周上,则等于( )
A、 B、 C、 D、无法确定19. 如图,AB是的弦,半径于点D, , 点P在圆周上,则等于( )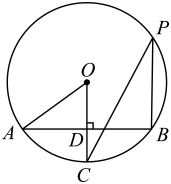 A、27° B、30° C、32° D、36°20. 如图,在中, , 若 , 则的度数为( )
A、27° B、30° C、32° D、36°20. 如图,在中, , 若 , 则的度数为( ) A、 B、 C、 D、21. 如图,是的直径,为弦, , 在上任取一点D,且点D与点C位于直径的两侧,连接和 , 则的度数是( )
A、 B、 C、 D、21. 如图,是的直径,为弦, , 在上任取一点D,且点D与点C位于直径的两侧,连接和 , 则的度数是( ) A、 B、 C、 D、22. 如图,点 , , 在 上, , ,连接 交 于点 ,则 的度数是( )
A、 B、 C、 D、22. 如图,点 , , 在 上, , ,连接 交 于点 ,则 的度数是( ) A、108° B、109° C、110° D、112°23. 已知 , , 是等圆, 内接于 ,点C , E分别在 , 上.如图,①以C为圆心, 长为半径作弧交 于点D , 连接 ;②以E为圆心, 长为半径作弧交 于点F , 连接 ;下面有四个结论:① ;② ;③ ;④ ,所有正确结论的个数是( )
A、108° B、109° C、110° D、112°23. 已知 , , 是等圆, 内接于 ,点C , E分别在 , 上.如图,①以C为圆心, 长为半径作弧交 于点D , 连接 ;②以E为圆心, 长为半径作弧交 于点F , 连接 ;下面有四个结论:① ;② ;③ ;④ ,所有正确结论的个数是( ) A、1个 B、2个 C、3个 D、4个24. 如图,是的直径,点 , 点是半圆上两点,连结 , 相交于点 , 连结 , 已知于点 , 下列结论:
A、1个 B、2个 C、3个 D、4个24. 如图,是的直径,点 , 点是半圆上两点,连结 , 相交于点 , 连结 , 已知于点 , 下列结论:
;若点为的中点,则.若 , 则;;其中正确的是( )
A、 B、 C、 D、四、第九题
-
25. 已知点 A(a,2)、B(b,2)、C(c,7)都在抛物线 上,点A在点B左侧,下列选项正确的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则26. 已知点 , 在抛物线(m是常数)上,若 , , 则下列大小比较正确的是( )A、 B、 C、 D、27. 已知是抛物线上的三点,则由小到大依序排列是( )A、 B、 C、 D、28. 已知点均在抛物线上,则a,b,c的大小关系为( )A、 B、 C、 D、29. 已知点A(3,a),B(-3,b)均在二次函数y=-(x-2)2+1的图象上,则a,b,1的大小关系正确的是( )A、1<a<b B、1<b<a C、b<a<1 D、a<b<130. 在下列函数图象上任取不同的两点P(x1 , y1), Q(x2 , y2), 一定能使的是( )A、y=(x>0) B、y=-(x-2)2+5(x≥0) C、y=(x-3)2-4(x<0) D、y=3x+731. 点P(x1 , y1),Q(x2 , y2)在抛物线y=ax2-4ax+2(a>0)上,若对于t<x1<t+1,t+2<x2<t+3,都有y1≠y2 , 则t的取值范围是( )A、t≥1 B、t≤0 C、t≥1或t≤0 D、t≥1或t≤-1
五、第十题
-
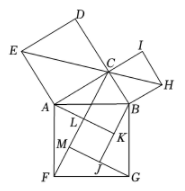
32. 如图,在 中, ,以其三边为边向外作正方形,连结 ,作 于点M, 于点J, 于点K,交 于点L.若正方形 与正方形 的面积之比为5, ,则 的长为( )
 A、 B、 C、 D、33. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.作.若 , 则的值为( )
A、 B、 C、 D、33. 由四个全等的直角三角形和一个小正方形组成的大正方形如图所示.作.若 , 则的值为( ) A、 B、 C、 D、134. 如图,在中, , 以 , 为边分别向外作正方形和正方形 , 交于点M,交于点N.若 , 则( )
A、 B、 C、 D、134. 如图,在中, , 以 , 为边分别向外作正方形和正方形 , 交于点M,交于点N.若 , 则( ) A、 B、 C、 D、135. 如图,已知正方形和正方形 , 点、分别为、的中点,连接和 , 则下列结论中:①;②为等腰三角形;③;④ , 正确的有多少个?( )
A、 B、 C、 D、135. 如图,已知正方形和正方形 , 点、分别为、的中点,连接和 , 则下列结论中:①;②为等腰三角形;③;④ , 正确的有多少个?( ) A、1个 B、2个 C、3个 D、4个36. 如图,正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.以下四个结论:①;②△AFC∽△AGD;③2AE2=AH•AC;④DG⊥AC.其中正确的个数为( )
A、1个 B、2个 C、3个 D、4个36. 如图,正方形ABCD中,点F是BC边上一点,连接AF,以AF为对角线作正方形AEFG,边FG与正方形ABCD的对角线AC相交于点H,连接DG.以下四个结论:①;②△AFC∽△AGD;③2AE2=AH•AC;④DG⊥AC.其中正确的个数为( ) A、1个 B、2个 C、3个 D、4个37. 如图,点C是线段AB上一点,且AC>BC,分别以AC,BC为边在线段AB的同侧作正方形ACDE和正方形CBFG,连结EF交GD于H,设正方形ACDE的周长和面积分别为C1 , S1 , 正方形CBFG的周长和面积分别为C2 , S2 , 下列一定能求出△DEH与△GFH面积差的条件是( )
A、1个 B、2个 C、3个 D、4个37. 如图,点C是线段AB上一点,且AC>BC,分别以AC,BC为边在线段AB的同侧作正方形ACDE和正方形CBFG,连结EF交GD于H,设正方形ACDE的周长和面积分别为C1 , S1 , 正方形CBFG的周长和面积分别为C2 , S2 , 下列一定能求出△DEH与△GFH面积差的条件是( ) A、S1-S2 B、S1+S2 C、C1-C2 D、C1+C238. 如图,在正方形ABCD中,点G为CD边上一点,以CG为边向右作正方形CEFG,连结AF,BD交于点P,连结BG,过点F作FH∥BG交BC于点H,连结AH,交BD于点K,下列结论中错误的是( )
A、S1-S2 B、S1+S2 C、C1-C2 D、C1+C238. 如图,在正方形ABCD中,点G为CD边上一点,以CG为边向右作正方形CEFG,连结AF,BD交于点P,连结BG,过点F作FH∥BG交BC于点H,连结AH,交BD于点K,下列结论中错误的是( ) A、HE=CD B、△AHF是等腰直角三角形 C、点P为AF中点 D、PK=BK+DP
A、HE=CD B、△AHF是等腰直角三角形 C、点P为AF中点 D、PK=BK+DP