鲁教版(五四制)2022-2023学年度第二学期八年级数学 矩形的性质与判定 期中复习
试卷更新日期:2023-04-14 类型:复习试卷
一、单选题
-
1. 如图,在矩形ABCD中,对角线AC、BD相交于点O,DE⊥AC于点E,∠AOD=110°,则∠CDE的大小是( )
 A、55° B、40° C、35° D、20°2. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以
A、55° B、40° C、35° D、20°2. 如图,在Rt△ABC中,∠BAC=90°,AB=AC=16cm,AD为BC边上的高.动点P从点A出发,沿A→D方向以 cm/s的速度向点D运动.设△ABP的面积为S1 , 长方形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=( )秒时,S1=2S2 .
cm/s的速度向点D运动.设△ABP的面积为S1 , 长方形PDFE的面积为S2 , 运动时间为t秒(0<t<8),则t=( )秒时,S1=2S2 .  A、5 B、6 C、7 D、83. 如图,在矩形中, , 点M在边上,若平分 , 则的长是( )
A、5 B、6 C、7 D、83. 如图,在矩形中, , 点M在边上,若平分 , 则的长是( ) A、 B、 C、 D、4. 在矩形中, , 对角线交于点O,则( )
A、 B、 C、 D、4. 在矩形中, , 对角线交于点O,则( ) A、3 B、4 C、5 D、105. 如图,在矩形ABCD中, , , 点E在AB延长线上,且 , 连接DE,则DE的长为( )
A、3 B、4 C、5 D、105. 如图,在矩形ABCD中, , , 点E在AB延长线上,且 , 连接DE,则DE的长为( ) A、6 B、 C、 D、86. 在矩形中, , , 将矩形沿折叠,点B落在点E处,线段交于定O,过O作于点G,于点H,则的值为( )
A、6 B、 C、 D、86. 在矩形中, , , 将矩形沿折叠,点B落在点E处,线段交于定O,过O作于点G,于点H,则的值为( ) A、1 B、 C、 D、7. 如图,将矩形ABCD沿直线DE折叠,顶点A落在BC边上F处,已知 , , 则BF的长为( )
A、1 B、 C、 D、7. 如图,将矩形ABCD沿直线DE折叠,顶点A落在BC边上F处,已知 , , 则BF的长为( )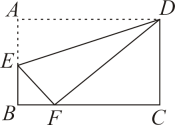 A、5 B、4 C、3 D、28. 如图,已知四边形是平行四边形,下列结论中正确的是( )
A、5 B、4 C、3 D、28. 如图,已知四边形是平行四边形,下列结论中正确的是( ) A、当时,它是矩形 B、当时,它是矩形 C、当时,它是正方形 D、当时,它是菱形9. 如图1,点为矩形边上的一个动点,点从出发沿着矩形的四条边运动,最后回到设点运动的路程长为 , 的面积为 , 图2是随变化的函数图象,则矩形的对角线的长是( )
A、当时,它是矩形 B、当时,它是矩形 C、当时,它是正方形 D、当时,它是菱形9. 如图1,点为矩形边上的一个动点,点从出发沿着矩形的四条边运动,最后回到设点运动的路程长为 , 的面积为 , 图2是随变化的函数图象,则矩形的对角线的长是( ) A、 B、 C、8 D、1010. 如图,在矩形ABCD中,AB=3,BC=4,连接BD,作∠CBD的平分线交CD于点E,则CE的长度为( )
A、 B、 C、8 D、1010. 如图,在矩形ABCD中,AB=3,BC=4,连接BD,作∠CBD的平分线交CD于点E,则CE的长度为( )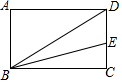 A、 B、2 C、3 D、4
A、 B、2 C、3 D、4二、填空题
-
11. 一个木匠要制作矩形的踏板.他在一个对边平行的长木板上分别沿与长边垂直的方向锯两次,就能得到矩形踏板.理由是 .
 12. 如图,矩形ABCD的对角线AC与BD交于点O,过点O作 , 交AD于点E,过点E作 , 垂足为F, , , , 则矩形ABCD的面积为 .
12. 如图,矩形ABCD的对角线AC与BD交于点O,过点O作 , 交AD于点E,过点E作 , 垂足为F, , , , 则矩形ABCD的面积为 . 13. 如图,O是矩形ABCD对角线AC的中点,E是AB上的一点,将沿CE折叠后,点B恰好与点O重合.若 , 则折痕CE的长为 .
13. 如图,O是矩形ABCD对角线AC的中点,E是AB上的一点,将沿CE折叠后,点B恰好与点O重合.若 , 则折痕CE的长为 . 14. 如图,在矩形ABCD中,EF为对角线BD的垂直平分线,分别交AD、BC于点E、F,连接AO,若 , , 则 .
14. 如图,在矩形ABCD中,EF为对角线BD的垂直平分线,分别交AD、BC于点E、F,连接AO,若 , , 则 . 15. 如图,点P是正方形 的对角线 上一点, ,垂足分别为点E , F , 连接 ,给出下列四个结论:① ;② ;③ ;④ 一定是等腰三角形.其中正确的结论序号是 .
15. 如图,点P是正方形 的对角线 上一点, ,垂足分别为点E , F , 连接 ,给出下列四个结论:① ;② ;③ ;④ 一定是等腰三角形.其中正确的结论序号是 .
三、解答题
-
16. 如图,在△ABC中,AB=AC,AD⊥BC于点D,过点B作AD的平行线交外角∠BAF的平分线于点E.求证:四边形ADBE是矩形.
 17. 如图,已知矩形ABCD,AB=4,AD=6,点E是BC的中点,将△DCE沿DE折叠得到ΔDC1E,连接BC1、CC1 , CC1与DE交于点G.求BC1的长度.
17. 如图,已知矩形ABCD,AB=4,AD=6,点E是BC的中点,将△DCE沿DE折叠得到ΔDC1E,连接BC1、CC1 , CC1与DE交于点G.求BC1的长度. 18. 如图,在矩形中,点E是的中点,交于点F,点M在上,连接 , 把延翻折.当点A的对应点恰好落在上时,求的度数.
18. 如图,在矩形中,点E是的中点,交于点F,点M在上,连接 , 把延翻折.当点A的对应点恰好落在上时,求的度数.
四、综合题
-
19. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=AC,连接AE、CE.
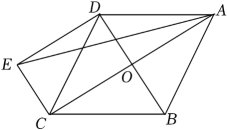 (1)、求证:四边形OCED为矩形;(2)、若菱形ABCD的边长为2,∠BCD=60°,求AE的长.20. 如图,一块长方形场地ABCD,现测得边长AB与AD之比为∶1,DE⊥AC于点E, BF⊥AC于点F,连接BE,DF.现计划在四边形DEBF区域内种植花草.
(1)、求证:四边形OCED为矩形;(2)、若菱形ABCD的边长为2,∠BCD=60°,求AE的长.20. 如图,一块长方形场地ABCD,现测得边长AB与AD之比为∶1,DE⊥AC于点E, BF⊥AC于点F,连接BE,DF.现计划在四边形DEBF区域内种植花草. (1)、求证:AE=EF=CF.(2)、求四边形DEBF与矩形ABCD的面积之比.21. 如图①,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F.
(1)、求证:AE=EF=CF.(2)、求四边形DEBF与矩形ABCD的面积之比.21. 如图①,将一张矩形纸片ABCD沿着对角线BD向上折叠,顶点C落到点E处,BE交AD于点F. (1)、求证:△BDF是等腰三角形.(2)、如图②,过点D作DG//BE,交BC于点G,连接FG交BD于点O.
(1)、求证:△BDF是等腰三角形.(2)、如图②,过点D作DG//BE,交BC于点G,连接FG交BD于点O.①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.

