鲁教版(五四制)2022-2023学年度第二学期八年级数学 菱形的性质与判定 期中复习
试卷更新日期:2023-04-14 类型:复习试卷
一、单选题
-
1. 在一组对边平行的四边形中,增加一个条件,使得这个四边形是菱形,那么增加的条件可以是( )A、另一组对边相等,对角线相等 B、另一组对边相等,对角线互相垂直 C、另一组对边平行,对角线相等 D、另一组对边平行,对角线相互垂直2. 如图,菱形ABCD的边长为6, , 点E是AB的中点,点P是对角线AC上一动点,则的最小值是( )
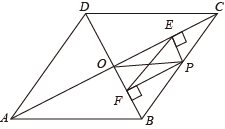
 A、 B、 C、3 D、3. 如图,菱形ABCD的对角线AC与BD交于点O,过点C作AB垂线交AB延长线于点E,连结OE,若AB=2 , BD=4,则OE的长为( )
A、 B、 C、3 D、3. 如图,菱形ABCD的对角线AC与BD交于点O,过点C作AB垂线交AB延长线于点E,连结OE,若AB=2 , BD=4,则OE的长为( ) A、6 B、5 C、2 D、44. 四边形是菱形, , , 对角线与相交于点 , 点在上,若 , 则( )A、 B、 C、或 D、45. 如图,菱形的周长是20, , 则对角线的长度为( )
A、6 B、5 C、2 D、44. 四边形是菱形, , , 对角线与相交于点 , 点在上,若 , 则( )A、 B、 C、或 D、45. 如图,菱形的周长是20, , 则对角线的长度为( ) A、5 B、 C、4 D、6. 如图,在菱形中,点是对角线上一动点,过点作于点 , 于点 . 若菱形的周长为48,面积为48,则的值为( )
A、5 B、 C、4 D、6. 如图,在菱形中,点是对角线上一动点,过点作于点 , 于点 . 若菱形的周长为48,面积为48,则的值为( ) A、6 B、5 C、4 D、37. 如图,菱形的边长为2, , 点为边的中点,点是对角线上的一动点,则的最小值为( )
A、6 B、5 C、4 D、37. 如图,菱形的边长为2, , 点为边的中点,点是对角线上的一动点,则的最小值为( )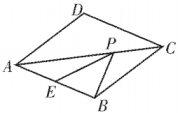 A、 B、 C、2 D、38. 如图,在菱形ABCD中, , ,点P、M分别是BD和BC上的动点,且点M与点B、C不重合,则 的最小值是( )
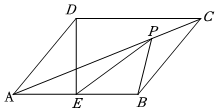
A、 B、 C、2 D、38. 如图,在菱形ABCD中, , ,点P、M分别是BD和BC上的动点,且点M与点B、C不重合,则 的最小值是( ) A、2 B、3 C、 D、49. 如图,在矩形ABCD中,对角线AC,BD相交于点E,BF∥AC,CF∥BD.若四边形BECF的面积为2,则矩形ABCD的面积为( )
A、2 B、3 C、 D、49. 如图,在矩形ABCD中,对角线AC,BD相交于点E,BF∥AC,CF∥BD.若四边形BECF的面积为2,则矩形ABCD的面积为( ) A、4 B、6 C、8 D、1610. 如图,在的两边上分别截取OA、OB,使;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC,连接AB、OC交于点D.若 , 四边形OACB的面积为.点E为CB的中点,连接DE,则线段DE的长为( )
A、4 B、6 C、8 D、1610. 如图,在的两边上分别截取OA、OB,使;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC,连接AB、OC交于点D.若 , 四边形OACB的面积为.点E为CB的中点,连接DE,则线段DE的长为( )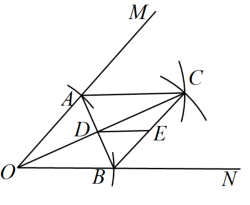 A、 B、 C、8 D、
A、 B、 C、8 D、二、填空题
-
11. 已知菱形中,对角线 , , 则与之间的距离是.12. 如图,在菱形中,与交于点O,若 , 则菱形的面积为 .
 13. 如图,在平面直角坐标系中,菱形OABC的顶点B的坐标为(8,4),则C点的坐标为 .
13. 如图,在平面直角坐标系中,菱形OABC的顶点B的坐标为(8,4),则C点的坐标为 . 14. 如图,在菱形中,对角线 , , 过A点作 , 则 .
14. 如图,在菱形中,对角线 , , 过A点作 , 则 .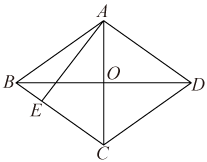 15. 如图,在菱形ABCD中,∠A=60°,E为AD中点,F为AB中点,若 , 则菱形ABCD的周长为 .
15. 如图,在菱形ABCD中,∠A=60°,E为AD中点,F为AB中点,若 , 则菱形ABCD的周长为 .
三、解答题
-
16. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,过点O作直线EF⊥BD,分别交AD、BC于点E和点F,求证:四边形BEDF是菱形.
 17. 如图,在菱形ABCD中,E为AB边上一点,过点E作 , 交BD于点M,交CD于点F.求证: .
17. 如图,在菱形ABCD中,E为AB边上一点,过点E作 , 交BD于点M,交CD于点F.求证: .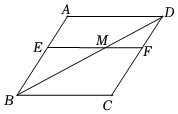 18. 如图,在 中, , 为 边上的中线,过点 作 ,过点 作 , 与 相交于点 .求证:四边形 为菱形.
18. 如图,在 中, , 为 边上的中线,过点 作 ,过点 作 , 与 相交于点 .求证:四边形 为菱形.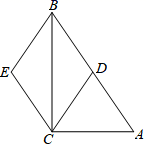
四、综合题
-
19. 如图,在菱形ABCD中,对角线AC、BD相交于点O,过点D作对角线BD的垂线交BA的延长线于点E.
 (1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求△ADE的周长.20. 如图,中, , 过点B作的平行线,与的平分线交于点D,点E是上一点,于点F,连接 .
(1)、证明:四边形ACDE是平行四边形;(2)、若AC=8,BD=6,求△ADE的周长.20. 如图,中, , 过点B作的平行线,与的平分线交于点D,点E是上一点,于点F,连接 . (1)、求证:四边形是菱形;(2)、若 , , 求的长.
(1)、求证:四边形是菱形;(2)、若 , , 求的长.