北师大版2022-2023学年度第二学期八年级数学一元一次不等式组期中复习

试卷更新日期：2023-04-14 类型：复习试卷

进入出卷网下载

一、单选题

1. 如图，数轴上表示的解集为（）

A、 $- 3 < x \leq 2$ B、 $x \leq 2$ C、 $x > - 3$ D、 $- 3 \leq x < 2$

查看试题解析
2. 在平面直角坐标系中，将点P （−x，1−x）先向右平移3个单位得点P₁ ，再将P₁向下平移3个单位得点P₂ ，若点P₂落在第四象限，则x的取值范围是（）

A、 $x > 3$ B、 $- 2 < x < 3$ C、 $x < - 2$ D、 $x < - 2$ 或 $x > 3$

查看试题解析
3. 若关于x的不等式组 ${\begin{array}{l} x - 2 \leq 3 a \\ x + 4 > a \end{array}$ 无解，则a的取值范围是（）

A、 $a$ ≤－3 B、 $a < - 3$ C、 $a > 3$ D、 $a$ ≥3

查看试题解析
4. 一元一次不等式组 ${\begin{array}{l} x + 3 \geq 2 \\ \frac{1}{2} x < 1 \end{array}$ 的解在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
5. 某运行程序如图所示，规定：从“输人一个值 $x$ ”到“结果是否大于95”为一次程序操作，如果程序操作进行了两次才停止，那么 $x$ 的取值范围是（）

A、 $x > 23$ B、 $23 < x \leq 47$ C、 $11 \leq x < 23$ D、 $x \leq 47$

查看试题解析
6. 若点P（a+1， $- \frac{1}{2}$ a+1）关于x轴对称的点在第一象限，则a的取值范围是（）

A、a＞﹣1 B、a＞2 C、﹣1＜a＜2 D、a＜2

查看试题解析
7. 若点P（ $- a$ ， $4 - a$ ）是第三象限的点，则a必须满足（）

A、 $a < 4$ B、 $a > 4$ C、 $a < 0$ D、 $0 < a < 4$

查看试题解析
8. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} \frac{1}{3} x > x - 2 \\ 4 x + 1 ⩾ a \end{array}$ 恰有4个整数解，且一次函数 $y = (a - 2) x + a + 5$ 不经过第三象限，则所有满足条件的整数 $a$ 的值之和是（）

A、-7 B、-12 C、-9 D、-11

查看试题解析
9. 非负数x，y满足 $y = - \frac{3}{2} x + \frac{7}{2}$ ， $w = 2 y - 3 x$ ，则w的最大值是（）

A、－7 B、 $\frac{7}{3}$ C、7 D、14

查看试题解析
10. 如果不等式组 ${\begin{array}{l} 2 x - m < 0 \\ 3 x - n > 0 \end{array}$ 的整数解仅为1，2，那么适合这个不等式组的整数 $m$ ， $n$ 的有序数对 $(m ， n)$ 共有（）

A、4个 B、6个 C、9个 D、12个

查看试题解析

二、填空题

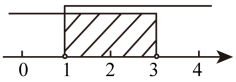
11. 某主题公园内一个活动项目的收费标准如下：个人票，每张10元；团体票，满20张八折优惠.当人数为时(人数不到20人)，买20人的团体票反而合算.

查看试题解析
12. 若关于x的不等式组 ${\begin{array}{l} \frac{x}{2} - 1 < \frac{2 - 3 x}{3} \\ a - 3 < 4 x - 2 \end{array}$ 有且仅有3个整数解，a的取值范围是.

查看试题解析
13. 已知A（m，y₁）、B（m+3，y₂）是反比例函数y＝ $\frac{2}{x}$ 图象上两点，且y₁﹣y₂＜0，则m的取值范围为．

查看试题解析
14. 如图，数轴上所表示的解集为.

查看试题解析
15. 已知关于x的不等式组 ${\begin{array}{l} x - a \geq b \\ 2 x - a < 2 b + 1 \end{array}$ 的解集为3≤x＜5，则 $\frac{a}{b}$ 的值为.

查看试题解析

三、解答题

16. 阿慧在店内购买两种蛋糕当伴手礼，如图为蛋糕的价目表.已知阿慧购买10盒蛋糕，花费的金额不超过2500元.若他将蛋糕分给75位同事，每人至少能拿到一个蛋糕，则阿慧花多少元购买蛋糕？

查看试题解析
17. 解不等式组 ${\begin{matrix} x + 2 > 0 \\ 2 x - 4 \leq 0 \end{matrix}$ 并将解集在数轴上表示

查看试题解析
18. 三个数 $1 - 2 a$ ， $a - 1$ ， 3在数轴上从左到右依次排列，求a的取值范围．

查看试题解析

四、综合题

19. 解不等式（组）.

(1)、解不等式： $\frac{2 x - 1}{3} - \frac{5 x + 1}{2} > 1$ ，

(2)、解不等式组 ${\begin{array}{l} x - 4 < 3 (x - 2) \\ \frac{1 + 2 x}{3} + 1 \geq x \end{array}$ ，并把它的解集表示在数轴上.

查看试题解析
20. 某养殖场计划今年养殖无公害标准化龙虾和鲤鱼，由于受养殖水面的制约，这两个品种的苗种的总投放量只有50吨.根据经验测算，这两个品种的种苗每投放一吨的先期投资、养殖期间的投资以及产值如下表：(单位：千元/吨)
品种
先期投资
养殖期间投资
产值
鲤鱼
9
3
30
龙虾
4
10
20
养殖场受经济条件的影响，先期投资不超过360千元，养殖期间的投资不超过290千元.设鲤鱼种苗的投放量为x吨.

(1)、求x的取值范围；

(2)、设这两个品种产出后的总产值为y(千元)，试写出y与x之间的函数关系式，并求出当x等于多少时，y有最大值?最大值是多少?

查看试题解析
21. 为做好新冠疫情的防控工作，某学校需购买甲、乙两种品牌的消毒液.经了解，每箱甲消毒液的售价比每箱乙消毒液的售价贵40元，且用1200元购买甲消毒液的数量恰好与用960元购买乙消毒液的数量相同.

(1)、求每箱甲、乙消毒液的售价分别是多少元?

(2)、若学校准备购买甲、乙两种消毒液共50箱(两种消毒液都购买)，且购买乙消毒液的箱数不多于甲消毒液箱数的 $\frac{2}{3}$ ，请问甲、乙消毒液分别购买多少箱时，所需总费用最少?最少总费用是多少?

查看试题解析
22. 已知等腰三角形的周长为24．

(1)、求底边长y关于腰长x的函数表达式；（x为自变量）

(2)、求自变量x的取值范围．

查看试题解析
23. 如图，在平面直角坐标系 $x O y$ 中，已知点 $A (5 ， 1)$ ， $B (1 ， 1)$ ， $C (0 ， 5)$ .直线m平行于x轴且经过C，D，E三点.直线l的关系式为 $y = - 2 x + b$ .

(1)、若 $△ A B D$ 是以 $A B$ 为底的等腰三角形，且直线l过点D，求b的值；

(2)、若 $b = 9$ ，直线l与 $▱ A B D E$ 的边 $D E$ 相交时，求点E的横坐标n的取值范围；

(3)、若点F为 $▱ A B D E$ 的对角线 $B E$ 与 $D A$ 的交点，当直线 $l$ 经过点F时，求点D的横坐标q与b之间的函数关系式.

查看试题解析

品种	先期投资	养殖期间投资	产值
鲤鱼	9	3	30
龙虾	4	10	20

北师大版2022-2023学年度第二学期八年级数学 一元一次不等式组 期中复习

一、单选题

二、填空题

三、解答题

四、综合题

北师大版2022-2023学年度第二学期八年级数学一元一次不等式组期中复习