北师大版2022-2023学年度第二学期八年级数学 一元一次不等式与一次函数 期中复习
试卷更新日期:2023-04-14 类型:复习试卷
一、单选题
-
1. 如图,直线y=x+m与y=nx-5n(n≠0)的交点的横坐标为3,则关于x的不等式x+m>nx-5n>0的整数解为( )
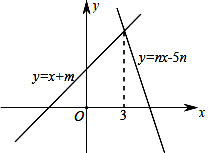 A、6 B、5 C、4 D、32. 直线与直线 , 在同一平面直角坐标系中的图象如图所示,则关于x的不等式的解集为( )
A、6 B、5 C、4 D、32. 直线与直线 , 在同一平面直角坐标系中的图象如图所示,则关于x的不等式的解集为( ) A、x<-1 B、x>-1 C、-1 <x<0 D、x>03. 一次函数y=kx+b的图象如图所示,那么不等式kx+b≤0的解是( ).
A、x<-1 B、x>-1 C、-1 <x<0 D、x>03. 一次函数y=kx+b的图象如图所示,那么不等式kx+b≤0的解是( ). A、 B、 C、 D、4. 如图,直线经过点 , 则关于x的不等式解集为( )
A、 B、 C、 D、4. 如图,直线经过点 , 则关于x的不等式解集为( )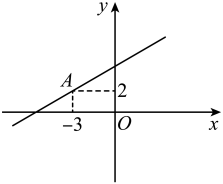 A、 B、 C、 D、5. 如图,直线过点A、B,则不等式的解集是( )
A、 B、 C、 D、5. 如图,直线过点A、B,则不等式的解集是( ) A、 B、 C、 D、6. 如图,直线与直线相交于点 , 则关于x的不等式的解为( )
A、 B、 C、 D、6. 如图,直线与直线相交于点 , 则关于x的不等式的解为( ) A、 B、 C、 D、7. 如图,直线交y轴于点A,交x轴于点B,且 , 不等式的解集为( )
A、 B、 C、 D、7. 如图,直线交y轴于点A,交x轴于点B,且 , 不等式的解集为( )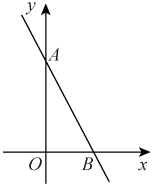 A、 B、x>3 C、 D、x<38. 一次函数y=kx+b的图象如图所示,当kx+b>3时,x的取值范围是( )
A、 B、x>3 C、 D、x<38. 一次函数y=kx+b的图象如图所示,当kx+b>3时,x的取值范围是( )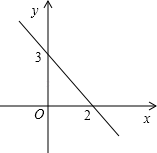 A、x>0 B、x<0 C、x<2 D、x>29. 如图,直线与直线相交于点A,点A的纵坐标为1,则不等式的解集为( )
A、x>0 B、x<0 C、x<2 D、x>29. 如图,直线与直线相交于点A,点A的纵坐标为1,则不等式的解集为( ) A、 B、 C、 D、10. 一次函数和的图象如图所示,下列结论:
A、 B、 C、 D、10. 一次函数和的图象如图所示,下列结论:
① ;② ;③方程的解是;④不等式的解集
其中正确的个数是( )
A、1 B、2 C、3 D、4二、填空题
-
11. 如图,直线 y=kx+b交 x 轴于点 A(-3,0),交 y 轴于点 B(0,4),则 0<kx+b<4的解集为.
 12. 如图,已知直线和直线的交点坐标是(m,n),则关于x的不等式的解集是 .
12. 如图,已知直线和直线的交点坐标是(m,n),则关于x的不等式的解集是 . 13. 如图,已知,直线y=kx与直线y=ax+4交于点A(2,1),则不等式ax+4>kx的解集为 .
13. 如图,已知,直线y=kx与直线y=ax+4交于点A(2,1),则不等式ax+4>kx的解集为 .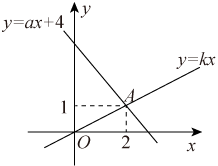 14. 如图,已知函数y=x+b和y=ax+3的图象交点为P,则不等式x+b<ax+3的解集为 .
14. 如图,已知函数y=x+b和y=ax+3的图象交点为P,则不等式x+b<ax+3的解集为 . 15. 平面直角坐标系中,直线与相交于点 , 下列结论中正确的是(填写序号).
15. 平面直角坐标系中,直线与相交于点 , 下列结论中正确的是(填写序号).
①关于x,y的方程组的解是;
②关于x的不等式的解集是;
③ .
三、解答题
-
16. 由于灯管老化,现某学校要购进A、B两种节能灯管320只,A、B两种灯管的单价分别为25元和30元,现要求B种灯管的数量不少于A种灯管的3倍,那么购买A种灯管多少只时,可使所付金额最少?最少为多少元?17. 直线 过点 ,直线 过点 ,求不等式 的解集.18. 已知一次函数 ,当 时, ,求此一次函数的表达式.
四、综合题
-
19. 如图,直线y=kx+b经过点A(-5,0),B(-1,4).
 (1)、求直线AB的表达式;(2)、若直线y=-2x-4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式kx+b>-2x-4的解集.20. 已知一次函数的图像与轴的交点在轴的上方,且随 的增大而减小.(1)、求整数的值;(2)、在(1)的结论下,在下面的平面直角坐标系中画出函数的图象,并根据图像回答:当取何值时,? ? ?
(1)、求直线AB的表达式;(2)、若直线y=-2x-4与直线AB相交于点C,求点C的坐标;(3)、根据图象,写出关于x的不等式kx+b>-2x-4的解集.20. 已知一次函数的图像与轴的交点在轴的上方,且随 的增大而减小.(1)、求整数的值;(2)、在(1)的结论下,在下面的平面直角坐标系中画出函数的图象,并根据图像回答:当取何值时,? ? ? 21. 如图,函数和的图象相交于点 .
21. 如图,函数和的图象相交于点 .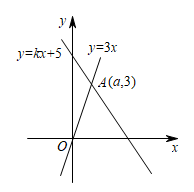 (1)、求a,k的值;(2)、根据图象,直接写出不等式的解集.
(1)、求a,k的值;(2)、根据图象,直接写出不等式的解集.