北师大版2022-2023学年度第二学期八年级数学 中心对称 期中复习
试卷更新日期:2023-04-14 类型:复习试卷
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
2. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 在以下“绿色食品、响应环保、可回收物、节水”四个图案中,是中心对称图形的是( )A、
3. 在以下“绿色食品、响应环保、可回收物、节水”四个图案中,是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 4. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
4. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 5. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、
5. 下列图形中,既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 围棋起源于中国.古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )A、
6. 围棋起源于中国.古代称之为“弈”,至今已有4000多年历史.2017年5月,世界围棋冠军柯洁与人工智能机器人AlphaGo进行了围棋人机大战.截取对战机棋谱中的四个部分,由黑白棋子摆成的图案是中心对称图形的是( )A、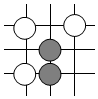 B、
B、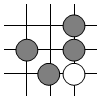 C、
C、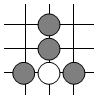 D、
D、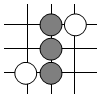 7. 面对新冠病毒疫情,我国毫不动摇坚持动态清零总方针,外防输人,内防反弹,下面是支付宝“国案政务服务平台”中关于疫情防控的四个小程序图标,其中的图案既是轴对称图形,又是中心对称图形的是( )A、
7. 面对新冠病毒疫情,我国毫不动摇坚持动态清零总方针,外防输人,内防反弹,下面是支付宝“国案政务服务平台”中关于疫情防控的四个小程序图标,其中的图案既是轴对称图形,又是中心对称图形的是( )A、 各地疫情风险等级查询
B、
各地疫情风险等级查询
B、 扫一扫防疫信息码
C、
扫一扫防疫信息码
C、 核酸和抗体检测查询
D、
核酸和抗体检测查询
D、 医用口罩信息查询
8. 下列图形中,不是中心对称图形的是( )A、
医用口罩信息查询
8. 下列图形中,不是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 9. 许多数学符号蕴含着对称美,在下列数学符号中,既是轴对称图形,又是中心对称图形的符号是( )A、
9. 许多数学符号蕴含着对称美,在下列数学符号中,既是轴对称图形,又是中心对称图形的符号是( )A、 B、
B、 C、
C、 D、
D、 10. 下列图形中既是中心对称图形,又是轴对称图形是( )
10. 下列图形中既是中心对称图形,又是轴对称图形是( ) A、圆 B、平行四边形 C、等边三角形 D、等腰直角三角形
A、圆 B、平行四边形 C、等边三角形 D、等腰直角三角形二、填空题
-
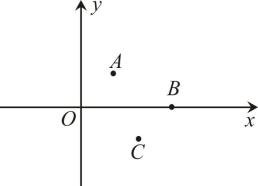
11. 如图,在平面直角坐标系中,点A,B,C的坐标分别为 , , . 点M从坐标原点O出发,第一次跳跃到点 , 使得点与点O关于点A成中心对称;第二次跳跃到点 , 使得点与点关于点B成中心对称;第三次跳跃到点 , 使得点与点关于点C成中心对称;第四次跳跃到点 , 使得点与点关于点A成中心对称;…,依此方式跳跃,点的坐标是 .
 12. 如图,已知 AB=3,AC=1,∠D=90°,△DEC 与△ABC关于点C成中心对称,则AE的长是 .
12. 如图,已知 AB=3,AC=1,∠D=90°,△DEC 与△ABC关于点C成中心对称,则AE的长是 .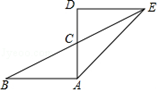 13. 已知点A(-1,2)与点B(3,4)是成中心对称的图形上的两个对称点,则对称中心的坐标为。14. 在方格纸中,选择标有序号①、②、③、④中的一个小正方形涂黑,能与图中阴影部分构成中心对称图形的小正方形的序号是。
13. 已知点A(-1,2)与点B(3,4)是成中心对称的图形上的两个对称点,则对称中心的坐标为。14. 在方格纸中,选择标有序号①、②、③、④中的一个小正方形涂黑,能与图中阴影部分构成中心对称图形的小正方形的序号是。 15. 点P(1,2)关于点Q(-1.1)对称的点的坐标为。
15. 点P(1,2)关于点Q(-1.1)对称的点的坐标为。三、解答题
-
16. 如图,在 中,∠ACB=90°,M为A B的中点,∠PMQ=90° ,试判断线段PQ,AP,BQ之间的数量关系,并说明理由
 17. 如图,在△ABC中,∠A=90°,点D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试写出线段BE,EF,FC之间的数量关系,并说明理由.
17. 如图,在△ABC中,∠A=90°,点D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试写出线段BE,EF,FC之间的数量关系,并说明理由. 18. 用直尺和圆规作图:已知△ABC与△A'B'C'成中心对称(点A与A'对应,点B与B'对应),请在图中画出对称中心O,并画出完整的△A'B'C'.(保留作图痕迹)
18. 用直尺和圆规作图:已知△ABC与△A'B'C'成中心对称(点A与A'对应,点B与B'对应),请在图中画出对称中心O,并画出完整的△A'B'C'.(保留作图痕迹)
四、综合题
-
19. 如图,在平面直角坐标系中,三个顶点的坐标分别为A(1,-4),B(5,-4),C(4,-1).

( 1 )画出关于原点O成中心对称的;
( 2 )画出绕点O逆时针旋转90°所得到的 , 并写出的坐标;
( 3 )将先向右平移2个单位长度,再向上平移6个单位长度,画出第二次平移后的 , 并写出的坐标.
20. 下列三幅图中的网格均由边长为1的小正方形组成,图1是三国时期吴国的数学家赵爽所绘制的“弦图”,它由四个形状、大小完全相同的直角三角形组成,赵爽利用这“弦图”对勾股定理作出了证明,是中国古代数学的一项重要成就,请根据下列要求解答问题. (1)、图1中“弦图”的四个直角三角形组成的图形(阴影部分)是(填“轴”或“中心”)对称图形;(2)、将“弦图”中的一个直角三角形作为基本图形,通过你所学过的图形变换知识,按下列要求画图:
(1)、图1中“弦图”的四个直角三角形组成的图形(阴影部分)是(填“轴”或“中心”)对称图形;(2)、将“弦图”中的一个直角三角形作为基本图形,通过你所学过的图形变换知识,按下列要求画图:①在图2中画出Rt△ABC向右平移4格后得到的△DEF;
②在图3中画出Rt△ABC绕点C顺时针旋转90°后得到的 .
21. 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后, 的顶点均在格点上,坐标分别为 , , .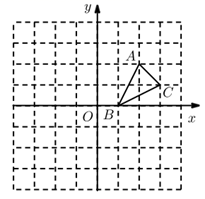 (1)、画出 关于x轴对称的 ;(2)、画出将 绕原点O逆时针旋转90°所得的 ;(3)、 与 成中心对称图形吗?若成中心对称图形,直接写出对称中心的坐标.22. 如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1 , D三点的坐标分别是(0,4),(0,3),(0,2).
(1)、画出 关于x轴对称的 ;(2)、画出将 绕原点O逆时针旋转90°所得的 ;(3)、 与 成中心对称图形吗?若成中心对称图形,直接写出对称中心的坐标.22. 如图,正方形ABCD与正方形A1B1C1D1关于某点中心对称,已知A,D1 , D三点的坐标分别是(0,4),(0,3),(0,2).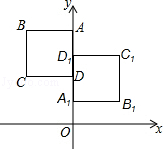 (1)、求对称中心的坐标.(2)、写出顶点B,C,B1 , C1的坐标.23. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).
(1)、求对称中心的坐标.(2)、写出顶点B,C,B1 , C1的坐标.23. 如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-3,2),B(0,4),C(0,2).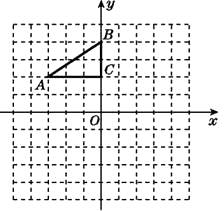 (1)、将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2.
(1)、将△ABC以点C为旋转中心旋转180°,画出旋转后对应的△A1B1C;平移△ABC,若点A的对应点A2的坐标为(0,-4),画出平移后对应的△A2B2C2.
(2)、若将△A1B1C绕某一点旋转可以得到△A2B2C2 , 请直接写出旋转中心的坐标.(3)、在x轴上有一点P,使得PA+PB的值最小,请直接写出点P的坐标.