2023年沪科版数学八年级下册期中测试模拟卷（二）

试卷更新日期：2023-04-14 类型：期中考试

进入出卷网下载

一、单选题（每题4分，共40分）

1. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{3}$ B、 $\sqrt{\frac{1}{5}}$ C、 $\sqrt{0.8}$ D、 $\sqrt{9}$

查看试题解析
2. 一个多边形的每一个外角均为40°，则这个多边形是 ( ）

A、八边形 B、九边形 C、十边形 D、十一边形

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{2} \cdot \sqrt{\frac{1}{2}} = 1$ B、 $\sqrt[3]{4} - \sqrt[3]{3} = 1$ C、 $\sqrt{6} \div \sqrt{3} = 2$ D、 $\sqrt{4} = \pm 2$

查看试题解析
4.
在直线l上依次摆放着七个正方形(如图所示)。已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S₁、S₂、S₃、S₄ ，则S₁＋S₂＋S₃＋S₄的值为（　　）

A、6 B、5 C、4 D、3

查看试题解析
5. 如果最简二次根式 $\sqrt{a + 2}$ 与 $\sqrt{12}$ 能够合并，那么a的值为（）

A、1 B、2 C、4 D、10

查看试题解析
6. 如图，长方体ABCD-A'B'C'D'是个无上底长方体容器，长AB＝5cm，宽BC＝3cm，高AA′＝8cm，甜食点M在容器内侧，位于侧棱BB′的中点，一只蚂蚁从容器外部的A爬到点M处吃甜食，这只蚂蚁爬行的最短路径是（）cm

A、 $\sqrt{41} + 5$ B、13 C、 $\sqrt{89} + 4$ D、14

查看试题解析
7. 若一元二次方程 $a x^{2} - x + 2 = 0$ 有两个不相等的实数根，则实数a的取值范围为（）

A、 $a < \frac{1}{8}$ B、 $a < \frac{1}{8}$ 且 $a \neq 0$ C、 $a \leq \frac{1}{8}$ 且 $a \neq 0$ D、 $a > \frac{1}{8}$

查看试题解析
8. 如图1，将一张长20cm，宽10cm的长方形硬纸片裁剪掉图中阴影部分之后，恰好折成如图2的有盖长方体纸盒，纸盒底面积为 $48 c m^{2}$ ，则该有盖纸盒的高为（）

A、4cm B、3cm C、2cm D、1cm

查看试题解析
9.
如图，在△ABC中，AB＝AC=BD，AD=CD，则∠ADB的度数是（）

A、36° B、45° C、60° D、72°

查看试题解析
10. 对于一元二次方程ax²+bx+c=0(a≠0)，下列说法：
①若 $\frac{a}{c}$ + $\frac{b}{c}$ =-1，则方程ax²+bx+c=0 一定有一根是x=1；
②若c=a³ ， b=2a² ，则方程ax²+bx+c=0有两个相等的实数根；
③若a<0，b<0，c>0，则方程cx²+bx+a=0必有实数根；
④若ab-bc=0且 $\frac{a}{c}$ <-l，则方程cx²+bx+a=0的两实数根一定互为相反数．．
其中正确的结论是( )

A、①②③④ B、①②④ C、①③ D、②④

查看试题解析

二、填空题（每题5分，共25分）

11. 要使式子有 $\frac{\sqrt{a + 3}}{a^{2} - 1}$ 意义，则a的取值范围是．

查看试题解析
12. 直角三角形两条边长分别为3和4，则第三边的长为.

查看试题解析
13. 已知 $x = 2$ 是方程 $x^{2} - 6 x + m = 0$ 的根，则该方程的另一根为.

查看试题解析
14. 《九章算术》是古代东方数学代表作，汇集了我国历代学者的劳动和智慧，被誉为人类科学史上应用数学的“算经之首”．其中记录了这样一个问题，原文：今有竹高一丈，末折抵地，去本三尺．问折者高几何？意思是：今有竹高10尺，末端被折断而抵达地面，离竹根部有3尺，则竹的余高为尺．

查看试题解析
15. 如图，在锐角△ABC中，∠BAC=45°，AB=2，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是．

查看试题解析

三、计算题（共2题，共20分）

16. 解方程

(1)、x²+2x=3x+6

(2)、x²-2x-7=0

查看试题解析
17. 计算：

(1)、 $\sqrt{3} (\sqrt{8} - \sqrt{2} + \sqrt{3 \frac{1}{3}})$

(2)、 ${(\sqrt{6} + \sqrt{3})}^{2} - {(\sqrt{6} - \sqrt{3})}^{2}$

查看试题解析

四、作图题（共10分）

18. 如图，边长为1的正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的
三角形叫做格点三角形．

(1)、请在正方形网格中画出格点△ABC，使AB= $\sqrt{5}$ ，BC= $\sqrt{10}$ ，AC= $\sqrt{13}$ ；

(2)、求AC边上的高．

查看试题解析

五、解答题（共5题，共55分）

19. 阅读材料：小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方．如3+2 $\sqrt{2} = {(1 + \sqrt{2})}^{2}$ ，善于思考的小明进行了以下探索，若设a+b $\sqrt{2} = {(m + n \sqrt{2})}^{2} = m^{2} + 2 n^{2} + 2 m n \sqrt{2}$ （其中，a，b，m，n均为整数），则有a＝m²+2n² ， b＝2mn，这样小明就找到一种把类似a+b $\sqrt{2}$ 的式子化为平方式的方法．请你依照小明的方法探索并解决下列问题：

(1)、若a+b $\sqrt{7} = {(m + n \sqrt{7})}^{2}$ ，当a，b，m，n均为整数时，用含m，n的式子分别表示a，b，得：a＝， b＝．

(2)、若a+6 $\sqrt{3} = {(m + n \sqrt{3})}^{2}$ ，当a，m，n均为正整数时，求a的值．

(3)、化简： $\sqrt{7 - 4 \sqrt{3}}$ 和 $\sqrt{5 + 2 \sqrt{6}}$ ．

查看试题解析
20. 今年第6号台风“烟花”登录我国沿海地区，风力强，累计降雨量大，影响范围大，有极强的破坏力.如图，台风“烟花”中心沿东西方向AB由A向B移动，已知点C为一海港，且点C与直线AB上的两点A、B的距离分别为AC＝300km，BC＝400km，又AB＝500km，经测量，距离台风中心260km及以内的地区会受到影响.

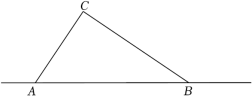(1)、求∠ACB的度数；

(2)、海港C受台风影响吗？为什么？

(3)、若台风中心的移动速度为28千米/时，则台风影响该海港持续的时间有多长？

查看试题解析
21. 如果关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 有两个实数根，且其中一个根为另一个根的2倍，那么称这样的方程为“倍根方程”．例如，一元二次方程 $x^{2} - 9 x + 18 = 0$ 的两个根是3和6，则方程 $x^{2} - 9 x + 18 = 0$ 就是“倍根方程”．

(1)、若一元二次方程 $x^{2} - 6 x + k = 0$ 是“倍根方程”，则 $k =$ ；

(2)、若一元二次方程 $n x^{2} - (2 n + m) x + 2 m = 0 (n \neq 0)$ 是“倍根方程”，求 $\frac{m + n}{2 m - n}$ 的值；

查看试题解析
22. 某商店通过网络在一源头厂家进一种季节性小家电，由于疫情影响以及市场竞争，该厂家不得不逐年下调出厂价；

(1)、2019年这个小家电出厂价是每台62.5元，到2021年同期该品牌小家电出厂价下调为40元，若每年下调幅度相同，请你计算该小家电出厂价平均每年下调的百分率；

(2)、若明年商场计划按每台40元购一批该品牌小家电，经市场预测，销售定价为50元时，每月可售出500台，销售定价每增加1元，销售量将减少10台．因受库存的影响，每月进货台数不得超过300台；商家若希望月获利8750元，则应进货多少台？销售定价多少元？

查看试题解析
23. 如图，△ABC中，∠C=90°，AB=5cm，BC=3cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设运动时间为t秒．

(1)、动点P运动2秒后，求△ABP的周长．

(2)、问t满足什么条件时，△BCP为直角三角形？

(3)、另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？

查看试题解析