北师大版2022-2023学年度第二学期八年级数学 等腰三角形 期中复习
试卷更新日期:2023-04-14 类型:复习试卷
一、单选题
-
1. 如图,在等边中, , 垂足为D,且 , 则的长为( )
 A、1 B、 C、2 D、2. 等腰三角形的一个角是50°,则它的底角是( )A、50° B、50°或65° C、80°或50° D、65°3. 如图,点A,B,C在一条直线上,△ABD和△BCE是等边三角形,连接AE和CD交于点M,则∠AMC的度数为( )
A、1 B、 C、2 D、2. 等腰三角形的一个角是50°,则它的底角是( )A、50° B、50°或65° C、80°或50° D、65°3. 如图,点A,B,C在一条直线上,△ABD和△BCE是等边三角形,连接AE和CD交于点M,则∠AMC的度数为( ) A、135° B、120° C、105° D、90°4. 如图,在中, , , 以点C为圆心,长为半径作弧交于点D,分别以点A和点D为圆心,大于长为半径作弧,两弧相交于点E,作直线 , 交于点F,则的度数是( )
A、135° B、120° C、105° D、90°4. 如图,在中, , , 以点C为圆心,长为半径作弧交于点D,分别以点A和点D为圆心,大于长为半径作弧,两弧相交于点E,作直线 , 交于点F,则的度数是( ) A、 B、 C、 D、5. 若一个等腰三角形的周长是10,其中一边长为2,则这个等腰三角形底边的长度为( )A、2或6 B、6 C、2或8 D、26. 如图,矩形ABCD 的对角线AC与BD相交于点O,∠AOB=60°,AB=3,则OC等于( )
A、 B、 C、 D、5. 若一个等腰三角形的周长是10,其中一边长为2,则这个等腰三角形底边的长度为( )A、2或6 B、6 C、2或8 D、26. 如图,矩形ABCD 的对角线AC与BD相交于点O,∠AOB=60°,AB=3,则OC等于( ) A、3 B、3.5 C、4 D、57. 如图,AB,BC,CD,DE是四根长度均为5cm的小木棒,点A、C、E共线.若AC=6cm,CD⊥BC,则线段CE的长度是( )
A、3 B、3.5 C、4 D、57. 如图,AB,BC,CD,DE是四根长度均为5cm的小木棒,点A、C、E共线.若AC=6cm,CD⊥BC,则线段CE的长度是( )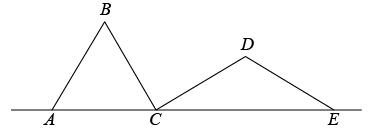 A、7cm B、6cm C、8cm D、8cm8. 用反证法证明命题“已知在中, , 则”时,首先应该假设( )A、 B、 C、 D、且9. 如图,是一钢架, , 为使钢架更加牢固,需在其内部添加一些钢管 , , , …,添加的钢管长度都与的长度相等,则最多能添加的钢管根数为( )
A、7cm B、6cm C、8cm D、8cm8. 用反证法证明命题“已知在中, , 则”时,首先应该假设( )A、 B、 C、 D、且9. 如图,是一钢架, , 为使钢架更加牢固,需在其内部添加一些钢管 , , , …,添加的钢管长度都与的长度相等,则最多能添加的钢管根数为( )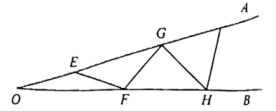 A、6 B、7 C、8 D、无数10. 如图,在中, , , 的垂直平分线交于点D,交于点E,交的延长线于点F,若 , 则的长为( )
A、6 B、7 C、8 D、无数10. 如图,在中, , , 的垂直平分线交于点D,交于点E,交的延长线于点F,若 , 则的长为( )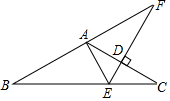 A、 B、2 C、 D、4
A、 B、2 C、 D、4二、填空题
-
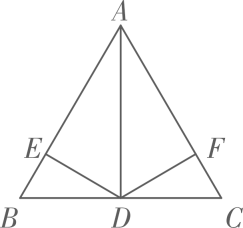
11. 如图,是等边三角形,AD是BC边上的高,点E是AC边的中点,点P是AD上的一个动点,当PC+PE最小时,∠CPE的度数是.
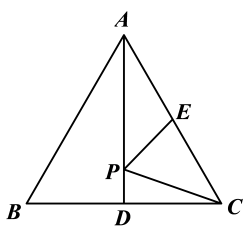 12. 若一个正三角形的路标的面积是 , 则它的边长为 .13. 如图,一艘船从A处出发向正北航行50海里到达B处,分别从A,B望灯塔C,测得 , , 则B处到灯塔C的距离是海里.
12. 若一个正三角形的路标的面积是 , 则它的边长为 .13. 如图,一艘船从A处出发向正北航行50海里到达B处,分别从A,B望灯塔C,测得 , , 则B处到灯塔C的距离是海里. 14. 等腰三角形的顶角度数为 , 则它的底角度数为 .15. 如图,用圆规以直角顶点O为圆心,以适当半径画一条弧交两直角边于A,B两点,若再以A点为圆心,以OA为半径画弧,与弧AB交于点C,则∠BOC等于 .
14. 等腰三角形的顶角度数为 , 则它的底角度数为 .15. 如图,用圆规以直角顶点O为圆心,以适当半径画一条弧交两直角边于A,B两点,若再以A点为圆心,以OA为半径画弧,与弧AB交于点C,则∠BOC等于 .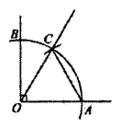
三、解答题
-
16. 如图,△ADC,△BCE都是正三角形求证:AE=BD.
 17. 如图,平分 , 垂足为点.求证:是等腰三角形.
17. 如图,平分 , 垂足为点.求证:是等腰三角形.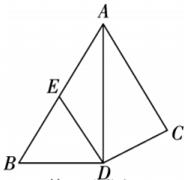 18. 如图, ,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.求证: .
18. 如图, ,∠A=90°,E是AB上的一点,且AD=BE,∠1=∠2.求证: .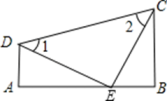
四、综合题
-
19. 如图,等腰三角形ABC的周长为20cm,底边BC长为y(cm),腰AB长为x(cm).
 (1)、求y与x之间的函数关系式;(2)、求x的取值范围;(3)、腰长AB=7时,底边的长.20. 在中, , , .
(1)、求y与x之间的函数关系式;(2)、求x的取值范围;(3)、腰长AB=7时,底边的长.20. 在中, , , .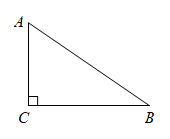 (1)、求线段的长;(2)、作边的垂直平分线分别交 , 于点和点(利用尺规作图,保留作图痕迹);(3)、连接 , 若 , 求的度数.
(1)、求线段的长;(2)、作边的垂直平分线分别交 , 于点和点(利用尺规作图,保留作图痕迹);(3)、连接 , 若 , 求的度数.