浙江省温州市普通高中2023届高三下学期数学3月第二次适应性考试试卷
试卷更新日期:2023-04-14 类型:高考模拟
一、单选题
-
1. 复数在复平面内对应的点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知随机变量服从正态分布 , 且 , 则( )A、 B、 C、 D、3. 展开式中二项式系数最大的是 , 则不可能是( )A、8 B、9 C、10 D、114. 某个函数的大致图象如图所示,则该函数可能是( )
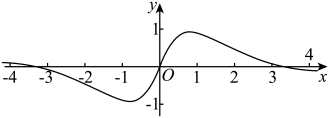 A、 B、 C、 D、5. 已知一个抛物线形拱桥在一次暴雨前后的水位之差是 , 暴雨后的水面宽为 , 暴雨来临之前的水面宽为 , 暴雨后的水面离桥拱顶的距离为( )A、 B、 C、 D、6. 一枚质地均匀的骰子,其六个面的点数分别为 . 现将此骰子任意抛掷2次,正面向上的点数分别为 . 设 , 设 , 记事件“”,“”,则( )A、 B、 C、 D、7. 已知 , 则( )A、 B、 C、 D、8. 已知正四棱锥的底面边长为 , 高为3.以点为球心,为半径的球与过点的球相交,相交圆的面积为 , 则球的半径为( )A、或 B、或 C、或 D、或
A、 B、 C、 D、5. 已知一个抛物线形拱桥在一次暴雨前后的水位之差是 , 暴雨后的水面宽为 , 暴雨来临之前的水面宽为 , 暴雨后的水面离桥拱顶的距离为( )A、 B、 C、 D、6. 一枚质地均匀的骰子,其六个面的点数分别为 . 现将此骰子任意抛掷2次,正面向上的点数分别为 . 设 , 设 , 记事件“”,“”,则( )A、 B、 C、 D、7. 已知 , 则( )A、 B、 C、 D、8. 已知正四棱锥的底面边长为 , 高为3.以点为球心,为半径的球与过点的球相交,相交圆的面积为 , 则球的半径为( )A、或 B、或 C、或 D、或二、多选题
-
9. 是等比数列的前项和,若存在 , 使得 , 则( )A、 B、是数列的公比 C、 D、可能为常数列10. 已知圆的方程为 , 对任意的 , 该圆( )A、圆心在一条直线上 B、与坐标轴相切 C、与直线不相交 D、不过点11. 蜜蜂是自然界的建筑大师,在18世纪初,法国数学家马拉尔迪指出,蜂巢是由许许多多类似正六棱柱形状的蜂房(如图)构成,其中每个蜂房的底部都是由三个全等的菱形构成,每个菱形钝角的余弦值是 , 则( )
 A、平面 B、 C、蜂房底部的三个菱形所在的平面两两垂直 D、该几何体的体积与以六边形为底面,以为高的正六棱柱的体积相等12. 函数 , 则( )A、 , 使得在上递减 B、 , 使得直线为曲线的切线 C、 , 使得既为的极大值也为的极小值 D、 , 使得在上有两个零点 , 且
A、平面 B、 C、蜂房底部的三个菱形所在的平面两两垂直 D、该几何体的体积与以六边形为底面,以为高的正六棱柱的体积相等12. 函数 , 则( )A、 , 使得在上递减 B、 , 使得直线为曲线的切线 C、 , 使得既为的极大值也为的极小值 D、 , 使得在上有两个零点 , 且三、填空题
-
13. 已知向量 , 若 , 则 .14. 已知抛物线和椭圆相交于两点,且抛物线的焦点也是椭圆的焦点,若直线过点 , 则椭圆的离心率是 .15. 平面内有四条平行线,相邻两条间距为1,每条直线上各取一点围成矩形,则该矩形面积的最小值是 .16. 若数列满足 , 则称此数列为“准等差数列”.现从这10个数中随机选取4个不同的数,则这4个数经过适当的排列后可以构成"准等差数列"的概率是 .
四、解答题
-
17. 已知三棱锥中,△是边长为3的正三角形,与平面所成角的余弦值为 .
 (1)、求证:;(2)、求二面角的平面角的正弦值.18. 已知是首项为1的等差数列,公差是首项为2的等比数列, .(1)、求的通项公式;(2)、若数列的第项 , 满足______(在①②中任选一个条件), , 则将其去掉,数列剩余的各项按原顺序组成一个新的数列 , 求的前20项和 .
(1)、求证:;(2)、求二面角的平面角的正弦值.18. 已知是首项为1的等差数列,公差是首项为2的等比数列, .(1)、求的通项公式;(2)、若数列的第项 , 满足______(在①②中任选一个条件), , 则将其去掉,数列剩余的各项按原顺序组成一个新的数列 , 求的前20项和 .①② .
19. 在一次全市的联考中,某校高三有100位学生选择“物化生”组合,100位学生选择“物化地”组合,现从上述的学生中分层抽取100人,将他们此次联考的化学原始成绩作为样本,分为6组: , 得到如图所示的频率分布直方图.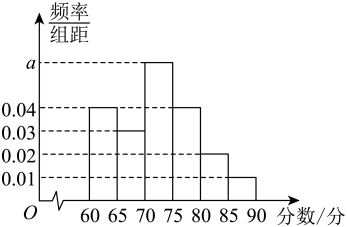
附: , 其中 .
0.10
0.05
0.01
0.001
2.706
3.841
6.635
10.828
(1)、求直方图中的值;(2)、在抽取的100位学生中,规定原始成绩不低于80分为“优秀”,低于80分为“不够优秀",请将下面的列联表补充完整,并判断是否有的把握认为成绩是否优秀与所选的组合有关?优秀
不够优秀
总计
“物化生”组合
40
“物化地”组合
总计
(3)、浙江省高考的选考科目采用等级赋分制,等级赋分的分差为1分,具体操作步骤如下:第一步:将原始成绩从高到低排列,按人数比例划分为20个赋分区间.
第二步:对每个区间的原始成绩进行等比例转换,公式为:
其中分别是该区间原始成绩的最低分、最高分;分别是该区间等级分的最低分、最高分;为某考生原始成绩,为转换结果.
第三步:将转换结果四舍五入,确定为该考生的最终等级分.
本次联考采用浙江选考等级赋分制,已知全市所有的考生原始成绩从高到低前(最低分为80分)的考生被划分至的赋分区间,甲、乙两位考生的化学原始成绩分别为 , 最终的等级分为98、99.试问:本次联考全市化学原始成绩的最高分是否可能是91分?请说明理由.
