浙江省杭州市2023届高三下学期数学教学质量检测(二模)试卷
试卷更新日期:2023-04-14 类型:高考模拟
一、单选题
-
1. 设集合 , , 则( )A、 B、 C、 D、2. 设复数z满足(i是虚数单位),则( )A、 B、 C、 D、3. 在数列中,“数列是等比数列”是“”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 已知平面向量 , , 且 , 则( )A、1 B、14 C、 D、5. 某兴趣小组研究光照时长x(h)和向日葵种子发芽数量y(颗)之间的关系,采集5组数据,作如图所示的散点图.若去掉后,下列说法正确的是( )
 A、相关系数r变小 B、决定系数变小 C、残差平方和变大 D、解释变量x与预报变量y的相关性变强6. 已知 , , 且 , 则ab的最小值为( )A、4 B、8 C、16 D、327. 如图,点、、、、为正方体的顶点或所在棱的中点,则下列各图中,不满足直线平面的是( )A、
A、相关系数r变小 B、决定系数变小 C、残差平方和变大 D、解释变量x与预报变量y的相关性变强6. 已知 , , 且 , 则ab的最小值为( )A、4 B、8 C、16 D、327. 如图,点、、、、为正方体的顶点或所在棱的中点,则下列各图中,不满足直线平面的是( )A、 B、
B、 C、
C、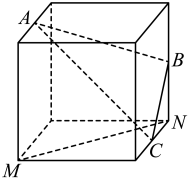 D、
D、 8. 已知满足 , 且在上单调,则的最大值为( )A、 B、 C、 D、
8. 已知满足 , 且在上单调,则的最大值为( )A、 B、 C、 D、二、多选题
-
9. 若直线与圆C:相交于A,B两点,则的长度可能等于( )A、2 B、3 C、4 D、510. 已知函数()是奇函数,且 , 是的导函数,则( )A、 B、的周期是4 C、是偶函数 D、11. 一口袋中有除颜色外完全相同的3个红球和2个白球,从中无放回的随机取两次,每次取1个球,记事件A1:第一次取出的是红球;事件A2:第一次取出的是白球;事件B:取出的两球同色;事件C:取出的两球中至少有一个红球,则( )A、事件 , 为互斥事件 B、事件B,C为独立事件 C、 D、12. 如图圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等, , 为圆柱上下底面的圆心,O为球心,EF为底面圆的一条直径,若球的半径 , 则( )
 A、球与圆柱的体积之比为 B、四面体CDEF的体积的取值范围为 C、平面DEF截得球的截面面积最小值为 D、若P为球面和圆柱侧面的交线上一点,则的取值范围为
A、球与圆柱的体积之比为 B、四面体CDEF的体积的取值范围为 C、平面DEF截得球的截面面积最小值为 D、若P为球面和圆柱侧面的交线上一点,则的取值范围为三、填空题
-
13. 在的展开式中,只有第5项的二项式系数最大,则展开式中含项的系数为14. 已知 , , 则 .15. 费马定理是几何光学中的一条重要原理,在数学中可以推导出圆锥曲线的一些光学性质.例如,点P为双曲线( , 为焦点)上一点,点P处的切线平分 . 已知双曲线C: , O为坐标原点,l是点处的切线,过左焦点作l的垂线,垂足为M,则 .16. 已知函数在点处的切线方程为l: , 若对任意 , 都有成立,则 .
四、解答题
-
17. 在中,内角A,B,C的对边分别为a,b,c,且 .(1)、求角B的大小;(2)、若 , 且AC边上的高为 , 求的周长.18. 设公差不为0的等差数列的前n项和为 , , .(1)、求数列的通项公式;(2)、若数列满足 , , 求数列的前n项和 .19. 在三棱锥中,底面为等腰直角三角形,.
 (1)、求证:;(2)、若 , 求平面与平面夹角的余弦值.20. 已知椭圆的离心率为 , 左、右顶点分别为、 , 点、为椭圆上异于、的两点,面积的最大值为 .(1)、求椭圆的方程;(2)、设直线、的斜率分别为、 , 且 .
(1)、求证:;(2)、若 , 求平面与平面夹角的余弦值.20. 已知椭圆的离心率为 , 左、右顶点分别为、 , 点、为椭圆上异于、的两点,面积的最大值为 .(1)、求椭圆的方程;(2)、设直线、的斜率分别为、 , 且 .①求证:直线经过定点.
②设和的面积分别为、 , 求的最大值.
21. 马尔科夫链是概率统计中的一个重要模型,也是机器学习和人工智能的基石,在强化学习、自然语言处理、金融领域、天气预测等方面都有着极其广泛的应用.其数学定义为:假设我们的序列状态是…, , , , , …,那么时刻的状态的条件概率仅依赖前一状态 , 即 .现实生活中也存在着许多马尔科夫链,例如著名的赌徒模型.
假如一名赌徒进入赌场参与一个赌博游戏,每一局赌徒赌赢的概率为 , 且每局赌赢可以赢得1元,每一局赌徒赌输的概率为 , 且赌输就要输掉1元.赌徒会一直玩下去,直到遇到如下两种情况才会结束赌博游戏:一种是手中赌金为0元,即赌徒输光;一种是赌金达到预期的B元,赌徒停止赌博.记赌徒的本金为 , 赌博过程如下图的数轴所示.

当赌徒手中有n元( , )时,最终输光的概率为 , 请回答下列问题:
(1)、请直接写出与的数值.(2)、证明是一个等差数列,并写出公差d.(3)、当时,分别计算 , 时,的数值,并结合实际,解释当时,的统计含义.22. 已知函数 .(1)、讨论函数零点个数;(2)、若恒成立,求a的取值范围.