四川省遂宁市2023届高三理数第二次诊断性考试试卷
试卷更新日期:2023-04-14 类型:高考模拟
一、单选题
-
1. 已知 , 则( )A、 B、 C、 D、2. 设全集为 , 集合 , , 则( )A、 B、 C、 D、3. 某乡镇为推动乡村经济发展,优化产业结构,逐步打造高品质的农业生产,在某试验区种植了某农作物.为了解该品种农作物长势,在实验区随机选取了100株该农作物苗,经测量,其高度(单位:cm)均在区间内,按照 , , , , 分成5组,制成如图所示的频率分布直方图,记高度不低于16cm的为“优质苗”.则所选取的农作物样本苗中,“优质苗”株数为( )
 A、20 B、40 C、60 D、884. 数学与音乐有着紧密的关联,我们平时听到的乐音一般来说并不是纯音,而是由多种波叠加而成的复合音.如图为某段乐音的图象,则该段乐音对应的函数解析式可以为( )
A、20 B、40 C、60 D、884. 数学与音乐有着紧密的关联,我们平时听到的乐音一般来说并不是纯音,而是由多种波叠加而成的复合音.如图为某段乐音的图象,则该段乐音对应的函数解析式可以为( ) A、 B、 C、 D、5. 已知 , , 则( )A、 B、 C、 D、6. 一个四棱台的三视图如图所示,其中正视图和侧视图均为上底长为2,下底长为4,腰长为2的等腰梯形,则该四棱台的体积为( )
A、 B、 C、 D、5. 已知 , , 则( )A、 B、 C、 D、6. 一个四棱台的三视图如图所示,其中正视图和侧视图均为上底长为2,下底长为4,腰长为2的等腰梯形,则该四棱台的体积为( )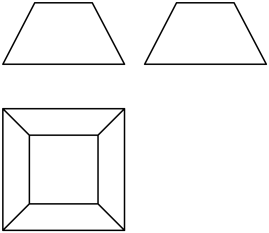 A、 B、 C、 D、567. 已知实数 , 满足 , 则下列各项中一定成立的是( )A、 B、 C、 D、8. 已知四棱柱的底面是正方形, , , 点在底面的射影为中点 , 则直线与平面所成角的正弦值为( )A、 B、 C、 D、9. 已知函数.给出下列结论:①是的最小值;②函数在上单调递增;③将函数的图象上的所有点向左平移个单位长度,可得到函数的图象.其中所有正确结论的序号是( )A、①② B、①③ C、②③ D、①②③10. 已知直线与抛物线交于点、 , 以线段为直径的圆经过定点 , 则( )A、4 B、6 C、8 D、1011. 在菱形中, , , 将绕对角线所在直线旋转至 , 使得 , 则三棱锥的外接球的表面积为( )A、 B、 C、 D、12. 若存在 , 使不等式成立,则的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、567. 已知实数 , 满足 , 则下列各项中一定成立的是( )A、 B、 C、 D、8. 已知四棱柱的底面是正方形, , , 点在底面的射影为中点 , 则直线与平面所成角的正弦值为( )A、 B、 C、 D、9. 已知函数.给出下列结论:①是的最小值;②函数在上单调递增;③将函数的图象上的所有点向左平移个单位长度,可得到函数的图象.其中所有正确结论的序号是( )A、①② B、①③ C、②③ D、①②③10. 已知直线与抛物线交于点、 , 以线段为直径的圆经过定点 , 则( )A、4 B、6 C、8 D、1011. 在菱形中, , , 将绕对角线所在直线旋转至 , 使得 , 则三棱锥的外接球的表面积为( )A、 B、 C、 D、12. 若存在 , 使不等式成立,则的取值范围是( )A、 B、 C、 D、二、填空题
-
13. 已知 , , , 则实数.14. 已知的展开式中含项的系数为 , 则.15. 已知为坐标原点,直线与双曲线的两条渐近线从左往右顺次交于两点.若 , 则双曲线的离心率为.16. 中,角、、所对的边分别为、、.若 , 且 , 则周长的最大值为.
三、解答题
-
17. 某商店销售某种产品,为了解客户对该产品的评价,现随机调查了200名客户,其评价结果为“一般”或“良好”,并得到如下列联表:
一般
良好
合计
男
20
100
120
女
30
50
80
合计
50
150
200
附表及公式:
0.15
0.10
0.05
0.025
0.010
2.072
2.706
3.841
5.024
6.635
其中 , .
(1)、通过计算判断,有没有99%的把握认为客户对该产品的评价结果与性别有关系?(2)、该商店在春节期间开展促销活动,该产品共有如下两个销售方案.方案一:按原价的8折销售;方案二:顾客购买该产品时,可在一个装有4张“每满200元少80元”,6张“每满200元少40元”共10张优惠券的不透明箱子中,随机抽取1张,购买时按照所抽取的优惠券进行优惠.已知该产品原价为260(元/件).顾客甲若想采用方案二的方式购买一件产品,估计顾客甲需支付的金额;你认为顾客甲选择哪种购买方案较为合理?18. 已知数列是公差为2的等差数列,.是公比大于0的等比数列, , .(1)、求数列和的通项公式;(2)、若数列满足 , 求的前项和.19. 如图,在三棱锥中,为的内心,直线与交于 , , .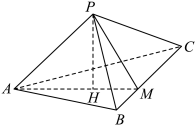 (1)、证明:平面平面;(2)、若 , , , 求二面角的余弦值.20. 已知椭圆经过 , 两点, , 是椭圆上异于的两动点,且 , 若直线 , 的斜率均存在,并分别记为 , .(1)、求证:为常数;(2)、求面积的最大值.
(1)、证明:平面平面;(2)、若 , , , 求二面角的余弦值.20. 已知椭圆经过 , 两点, , 是椭圆上异于的两动点,且 , 若直线 , 的斜率均存在,并分别记为 , .(1)、求证:为常数;(2)、求面积的最大值.