上海市崇明区2023届高三数学4月二模试卷

试卷更新日期：2023-04-14 类型：高考模拟

进入出卷网下载

一、填空题

1. 若不等式 $| x - 2 | < 1$ ，则x的取值范围是．

查看试题解析
2. 设复数z满足 $(1 + i) z = 2 i$ （i为虚数单位），则 $z =$ ．

查看试题解析
3. 已知集合 $A = {1 ， 2}$ ， $B = {a ， a^{2} + 1}$ ，若 $A \cap B = {1}$ ，则实数 $a$ 的值为.

查看试题解析
4. 已知函数 $y = s i n (2 ω x + φ)$ ， $(ω > 0)$ 的最小正周期为1，则 $ω =$ .

查看试题解析
5. 已知正实数a、b满足 $a b = 1$ ，则 $a + 4 b$ 的最小值等于．

查看试题解析
6. 在 $(x^{4} + \frac{1}{x})^{10}$ 的展开式中常数项是.（用数字作答）

查看试题解析
7. 以下数据为参加数学竞赛决赛的15人的成绩（单位：分），分数从低到高依次： $56 ， 70 ， 72 ， 78 ， 79 ， 80 ， 81 ， 83 ， 84 ， 86 ， 88 ， 90 ， 91 ， 94 ， 98$ ，则这15人成绩的第80百分位数是．

查看试题解析
8. 某单位为了了解用电量y度与气温x℃之间的关系，随机统计了某4天的用电量与当天气温．
气温（℃）
14
12
8
6
用电量（度）
22
26
34
38
由表中数据所得回归直线方程为 $y = - 2 x + \hat{b}$ ，据此预测当气温为5℃时，用电量的度数约为℃．

查看试题解析
9. 已知抛物线 $x^{2} = 2 y$ 上的两个不同的点 $A$ ， $B$ 的横坐标恰好是方程 $x^{2} + 6 x + 4 = 0$ 的根，则直线 $A B$ 的方程为．

查看试题解析
10. 在一个十字路口，每次亮绿灯的时长为30秒，那么，每次绿灯亮时，在一条直行道路上能有多少汽车通过？这个问题涉及车长、车距、车速、堵塞的干扰等多种因素，不同型号车的车长是不同的，驾驶员的习惯不同也会使车距、车速不同，行人和非机动车的干扰因素则复杂且不确定．面对这些不同和不确定，需要作出假设．例如小明发现虽然通过路口的车辆各种各样，但多数是小轿车，因此小明给出如下假设：通过路口的车辆长度都相等，请写出一个你认为合理的假设．

查看试题解析
11. 设平面向量 $\vec{a} ， \vec{b} ， \vec{c}$ 满足： $| \vec{a} | = 2$ ， $| \vec{b} | = | \vec{c} |$ ， $| \vec{a} - \vec{b} | = 1$ ， $\vec{b} ⊥ \vec{c}$ ，则 $| \vec{b} - \vec{c} |$ 的取值范围是．

查看试题解析
12. 若函数 $y = {\begin{array}{l} \frac{x^{3}}{e^{x}} ， x \geq 0 \\ a x^{2} ， x < 0 \end{array}$ 的图像上点 $A$ 与点 $B$ 、点 $C$ 与点 $D$ 分别关于原点对称，除此之外，不存在函数图象上的其它两点关于原点对称，则实数 $a$ 的取值范围是．

查看试题解析

二、单选题

13. 下列函数中，既是定义域内单调递增函数，又是奇函数的为（）

A、 $f (x) = t a n x$ B、 $f (x) = - \frac{1}{x}$ C、 $f (x) = x - c o s x$ D、 $f (x) = e^{x} - e^{- x}$

查看试题解析
14. 设两个正态分布 $N (μ_{1} ， σ_{1}^{2}) (σ_{1} > 0)$ 和 $N (μ_{2} ， σ_{2}^{2}) (σ_{2} > 0)$ 的密度函数图象如图所示．则有（）

A、 $μ_{1} < μ_{2} ， σ_{1} < σ_{2}$ B、 $μ_{1} < μ_{2} ， σ_{1} > σ_{2}$ C、 $μ_{1} > μ_{2} ， σ_{1} < σ_{2}$ D、 $μ_{1} > μ_{2} ， σ_{1} > σ_{2}$

查看试题解析
15. 《九章算术》中将底面为直角三角形且侧棱垂直于底面的三棱柱称为“堑堵”；底面为矩形，一条侧棱垂直于底面的四棱锥称之为“阳马”；四个面均为直角三角形的四面体称为“鳖臑”.如图，在堑堵 $A B C - A_{1} B_{1} C_{1}$ 中， $A C ⊥ B C$ ，且 $A A_{1} = A B = 2$ .下列说法错误的是（）

A、四棱锥 $B - A_{1} A C C_{1}$ 为“阳马” B、四面体 $A_{1} C_{1} C B$ 为“鳖臑” C、四棱锥 $B - A_{1} A C C_{1}$ 体积的最大值为 $\frac{2}{3}$ D、过A点作 $A E ⊥ A_{1} B$ 于点E，过E点作 $E F ⊥ A_{1} B$ 于点F，则 $A_{1} B ⊥$ 面AEF

查看试题解析
16. 已知数列 ${a_{n}}$ 是各项为正数的等比数列，公比为q，在 $a_{1} ， a_{2}$ 之间插入1个数，使这3个数成等差数列，记公差为 $d_{1}$ ，在 $a_{2} ， a_{3}$ 之间插入2个数，使这4个数成等差数列，公差为 $d_{2} ， ⋯$ ，在 $a_{n} ， a_{n + 1}$ 之间插入n个数，使这 $n + 2$ 个数成等差数列，公差为 $d_{n}$ ，则（）

A、当 $0 < q < 1$ 时，数列 ${d_{n}}$ 单调递减 B、当 $q > 1$ 时，数列 ${d_{n}}$ 单调递增 C、当 $d_{1} > d_{2}$ 时，数列 ${d_{n}}$ 单调递减 D、当 $d_{1} < d_{2}$ 时，数列 ${d_{n}}$ 单调递增

查看试题解析

三、解答题

17. 如图，已知点P在圆柱 $O_{1} O$ 的底面圆O的圆周上，AB为圆O的直径，圆柱的表面积为 $20 π$ ， $O A = 2$ ， $∠ A O P = 120 °$ ．

(1)、求直线 $A_{1} P$ 与平面 $A B P$ 所成角的大小；

(2)、求点 $A$ 到平面 $A_{1} B P$ 的距离．

查看试题解析
18. 在△ $A B C$ 中，a，b，c分别是内角A，B，C的对边， $\vec{m} = (2 a + c ， b)$ ， $\vec{n} = (c o s B ， c o s C)$ ， $\vec{m} \cdot \vec{n} = 0$ .

(1)、求角B大小；

(2)、设 $f (x) = 2 c o s x s i n (x + \frac{π}{3}) - 2 s i n^{2} x s i n B + 2 s i n x c o s x c o s (A + C)$ ，当 $x \in [\frac{π}{6} ， \frac{2 π}{3}]$ 时，求 $f (x)$ 的最小值及相应的x.

查看试题解析
19. 某校工会开展健步走活动，要求教职工上传3月1日至3月7日的微信记步数信息，下图是职工甲和职工乙微信记步数情况：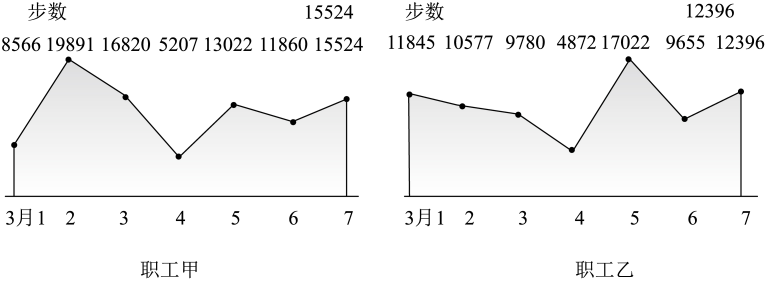

(1)、从3月2日至3月7日中任选一天，求这一天职工甲和职工乙微信记步数都不低于10000的概率；

(2)、从3月1日至3月7日中任选两天，记职工乙在这两天中微信记步数不低于10000的天数为 $X$ ，求 $X$ 的分布列及数学期望；

(3)、下图是校工会根据3月1日至3月7日某一天的数据制作的全校200名教职工微信记步数的频率分布直方图．已知这一天甲和乙微信记步数在单位200名教职工中排名（按照从大到小排序）分别为第68和第142，请指出这是根据哪一天的数据制作的频率分布直方图（不用说明理由）．

查看试题解析
20. 已知椭圆Γ： $\frac{x^{2}}{m^{2}} + \frac{y^{2}}{2} = 1 (m > 0 ， m \neq \sqrt{2})$ ，点 $A ， B$ 分别是椭圆Γ与 $y$ 轴的交点（点 $A$ 在点 $B$ 的上方），过点 $D (0 ， 1)$ 且斜率为 $k$ 的直线 $l$ 交椭圆 $Γ$ 于 $E ， G$ 两点．

(1)、若椭圆 $Γ$ 焦点在 $x$ 轴上，且其离心率是 $\frac{\sqrt{2}}{2}$ ，求实数 $m$ 的值；

(2)、若 $m = k = 1$ ，求 $△ B E G$ 的面积；

(3)、设直线 $A E$ 与直线 $y = 2$ 交于点 $H$ ，证明： $B ， G ， H$ 三点共线．

查看试题解析
21. 已知定义域为D的函数 $y = f (x)$ ，其导函数为 $y^{'} = f^{'} (x)$ ，满足对任意的 $x \in D$ 都有 $| f^{'} (x) | < 1$ ．

(1)、若 $f (x) = a x + l n x$ ， $x \in [1 ， 2]$ ，求实数a的取值范围；

(2)、证明：方程 $f (x) - x = 0$ 至多只有一个实根；

(3)、若 $y = f (x)$ ， $x \in R$ 是周期为2的周期函数，证明：对任意的实数 $x_{1}$ ， $x_{2}$ ，都有 $| f (x_{1}) - f (x_{2}) | < 1$ ．

查看试题解析

气温（℃）	14	12	8	6
用电量（度）	22	26	34	38