北师大版2022-2023学年度第二学期七年级数学 用关系式表示的变量间关系 期中复习
试卷更新日期:2023-04-14 类型:复习试卷
一、单选题
-
1. 有一个长为10,宽为6的长方形,若将长方形的宽增加 , 长不变,所得新长方形的面积y与x之间的关系式为( )A、 B、 C、 D、2. 若购买水性笔10支,花费20元,用y(元)表示购买水性笔的花费,x(支)表示水性笔的支数,那么y与x之间的关系式是( )A、 B、 C、 D、3. 长方形的周长为 , 其中一边的长为 , 面积为 , 则该长方形中与的关系式是( )A、 B、 C、 D、4. 已知圆柱的高为3 cm,当圆柱的底面半径r(cm)由小变大时,圆柱的体积V(cm3)随之变化,则V与r的关系式是 ( )A、V=πr2 B、V=9πr2 C、V= πr2 D、V=3πr25. 某次实验中,测得两个变量m和v之间的4组对应值如表,则m与之间的关系接近于下列各式中的( )
m
1
2
3
4
V
0.01
2.90
8.02
15.10
A、v=2m B、v=m²-1 C、v=3m+1 D、v=3m-16. 一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元,设门票的总费用为y元,则y与x的关系式为( ).A、 B、 C、 D、7. 在烧开水时,水温达到 水就会沸腾,下表是小红同学做“观察水的沸腾”实验时所记录的变量时间 和温度 的数据:0
2
4
6
8
10
12
14
…
30
44
58
72
86
100
100
100
…
在水烧开之前(即 ),温度 与时间 的关系式及因变量分别为( )
A、 , B、 , C、 , D、 ,8. 如果一盒圆珠笔有16支,售价24元,用y(元)表示圆珠笔的售价,x表示圆珠笔的支数,那么y与x间的关系式为( ).A、 B、 C、 D、9. 如图,李大爷用24米长的篱笆靠墙围成一个矩形 菜园,若菜园靠墙的一边 长为 (米),那么菜园的面积 (平方米)与 的关系式为( ) A、 B、 C、 D、10. 用100元钱在网上书店恰好可购买m本书,但是每本书需另加邮寄费6角,购买n本书共需费用y元,则可列出关系式( )A、 B、 C、 D、
A、 B、 C、 D、10. 用100元钱在网上书店恰好可购买m本书,但是每本书需另加邮寄费6角,购买n本书共需费用y元,则可列出关系式( )A、 B、 C、 D、二、填空题
-
11. 如图,三角形ABC的高AD=4,BC=6,点E在BC上运动,若设BE的长为三角形ACE的面积为有y,则y与x的关系式为.
 12. 若某长方体底面积是60( ),高为h(cm),则体积V( )与h(cm)之间的关系式为 .13. 某剧院的观众席的座位为扇形,且按下列方式设置:
12. 若某长方体底面积是60( ),高为h(cm),则体积V( )与h(cm)之间的关系式为 .13. 某剧院的观众席的座位为扇形,且按下列方式设置:排数()
1
2
3
4
…
座位数()
42
45
48
51
…
写出座位数与排数之间的关系式 .
14. 一台饮水机盛满20升水,打开阀门每分钟可流出0.5升水,饮水机中剩余水量y(升)与打开阀门时间x(分)之间的关系是.15. 如图,在中,边长为10,边上的高为6,点在上运动,设长为 , 则的面积与之间的关系式 .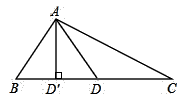
三、解答题
-
16. 中国联通在某地的资费标准为包月186元时,超出部分国内拨打0.36元/分,由于业务多,小明的爸爸打电话已超出了包月费.
下表是超出部分国内拨打的收费标准
时间/分
1
2
3
4
5
…
电话费/元
0.36
0.72
1.08
1.44
1.8
…
(1)这个表反映了哪两个变量之间的关系?哪个是自变量?
(2)如果用x表示超出时间,y表示超出部分的电话费,那么y与x的表达式是什么?
(3)如果打电话超出25分钟,需付多少电话费?
(4)某次打电话的费用超出部分是54元,那么小明的爸爸打电话超出几分钟?
17. 据测定,海底扩张的速度是很缓慢的,在太平洋海底,某海沟的某处宽度为100米,某两侧的地壳向外扩张的速度是每年6厘米,假设海沟扩张速度恒定,扩张时间为x年,海沟的宽度为y米.(1)写出海沟扩张时间x年与海沟的宽度y之间的表达式;
(2)你能计算以下当海沟宽度y扩张到400米时需要多少年吗?
四、综合题
-
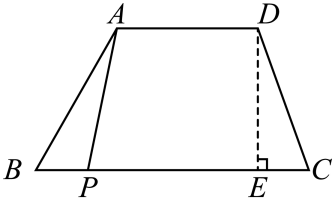
18. 如图,在梯形中, , , 高 , 点为边上任意一点,连接 , 当的长度由小到大变化时,四边形的面积也随之发生变化.
 (1)、在这个变化过程中,自变量、因变量分别是什么?(2)、若设 , 四边形的面积为 , 求与之间的关系式;(3)、当时,求四边形的面积.19. “五一”小长假期间,小天和父母一起开车到距家220千米的景点旅游,出发前,汽车油箱内储油45升,当行驶了180千米时,发现油箱余油量为27升(假设行驶过程中汽车的耗油量是均匀的).(1)、求该车平均每千米的耗油量;(2)、写出油箱余油量Q(升)与行驶路程x(千米)的关系式;(3)、当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前沿原路返回到家?请说明理由.20. 如图,梯形的上底长是5cm,下底长是13cm当梯形的高由大变小时,梯形的面积也随之发生变化.
(1)、在这个变化过程中,自变量、因变量分别是什么?(2)、若设 , 四边形的面积为 , 求与之间的关系式;(3)、当时,求四边形的面积.19. “五一”小长假期间,小天和父母一起开车到距家220千米的景点旅游,出发前,汽车油箱内储油45升,当行驶了180千米时,发现油箱余油量为27升(假设行驶过程中汽车的耗油量是均匀的).(1)、求该车平均每千米的耗油量;(2)、写出油箱余油量Q(升)与行驶路程x(千米)的关系式;(3)、当油箱中剩余油量低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前沿原路返回到家?请说明理由.20. 如图,梯形的上底长是5cm,下底长是13cm当梯形的高由大变小时,梯形的面积也随之发生变化. (1)、求梯形的面积y(cm2)与高x(cm)之间的表达式.(2)、当梯形的高由10cm变化到4cm时,则梯形的面积如何变化?21. 某公交车每天的支出费用为600元,每天的乘车人数x(人)与每天利润(利润=票款收入-支出费用)y(元)的变化关系,如下表所示(每位乘客的乘车票价固定不变): 表格中的字母P改为y:
(1)、求梯形的面积y(cm2)与高x(cm)之间的表达式.(2)、当梯形的高由10cm变化到4cm时,则梯形的面积如何变化?21. 某公交车每天的支出费用为600元,每天的乘车人数x(人)与每天利润(利润=票款收入-支出费用)y(元)的变化关系,如下表所示(每位乘客的乘车票价固定不变): 表格中的字母P改为y:x(人)
…
200
250
300
350
400
…
p(元)
…
-200
-100
0
100
200
…
根据表格中的数据,回答下列问题:
(1)、观察表中数据可知,当乘客量达到人以上时,该公交车才不会亏损;(2)、当一天乘客人数为500人时,利润是多少?(3)、请写出公交车每天利润y(元)与每天乘车人数x(人)的关系式.22. 为了解某种车的耗油量,我们对这种车在高速公路上做了耗油试验,并把试验的数据记录下来,制成如表:汽车行驶时间 t(小时)
0
1
2
3
…
油箱剩余油量 Q(升)
100
94
88
82
…
(1)、根据上表可知,该车油箱的大小为升,每小时耗油升;(2)、请求出两个变量之间的关系式(用t来表示Q).(3)、当汽车行驶12小时,邮箱还剩多少升油?23. 下表是某公共电话亭打长途电话的几次收费记录:时间x(分)
1
2
3
4
5
6
7
电话费y(元)
0.6
1.2
1.8
2.4
3.0
3.6
4.2
(1)、上表反映了哪两个变量间的关系?哪个是自变量?哪个是因变量?(2)、丽丽打了5分钟电话,那么电话费需付多少元?(3)、请写出y 与x之间的关系式.