2023年中考数学复习考点一遍过——数据分析

试卷更新日期：2023-04-14 类型：一轮复习

进入出卷网下载

一、单选题（每题3分，共30分）

1. 一组数据：3，2，x，6，5的平均数是4，则x的值是（）

A、3 B、4 C、5 D、6

查看试题解析
2. 据了解，某定点医院收治的6名“新型冠状肺炎”患者的新冠病毒潜伏期分别为2天，3天，3天，3天，4天，5天，则这6名患者新冠病毒潜伏期的众数为（　　）

A、2天 B、3天 C、4天 D、5天

查看试题解析
3. 一组数据0、 $- 3$ 、2、 $- 2$ 、1的极差是（　　）

A、2 B、3 C、4 D、5

查看试题解析
4. 已知一组数据a、b、c、d的平均数是3，在这组数据后再添加数据3得到一组新数据a、b、c、d、3，则新数据与原数据相比，方差将（）

A、不变 B、变大 C、变小 D、不能确定

查看试题解析
5. 王红同学在学校贯彻落实“双减”政策后，对本班同学一周七天，每天完成课外作业所用时间（平均时间）进行了调查统计，并将统计结果绘制成如图所示的折线统计图，则下列说法正确的是（）

A、每天完成课外作业所用时间的中位数是60分钟 B、每天完成课外作业所用时间的众数是45分钟 C、这一周完成课外作业所用时间的平均数是约为50分钟 D、每天完成课外作业所用时间的极差是70分钟

查看试题解析
6. 每年的4月23日是“世界读书日”．某中学为了了解八年级学生的读书情况，随机调查了50名学生的册数，统计数据如表所示：

册数

0

1

2

3

4

人数

3

13

16

17

1

则这50名学生读书册数的众数、中位数是（）

A、3，3 B、3，2 C、2，3 D、2，2

查看试题解析
7. 对甲、乙两同学100米短跑进行5次测试，他们的成绩通过计算得 ${\bar{x}}_{甲} = {\bar{x}}_{乙}$ ， $S_{甲}^{2} = 0.25$ ， $S_{乙}^{2} = 0.016$ ，下列说法正确的是（）

A、甲、乙两人的短跑成绩一样稳定 B、乙比甲的短跑成绩稳定 C、甲比乙的短跑成绩稳定 D、无法确定谁的短跑成绩更稳定

查看试题解析

8. 甲、乙、丙、丁，四名射击运动员进行射击测试，每人10次射击成绩的平均数x（单位：环）及方差

s^{2}

（单位：环）如下表所示：

	甲	乙	丙	丁
$x$	$7$	$8$	$9$	$8$
$s^{2}$	$1.7$	$0.9$	$0.6$	$1.2$

根据表中数据，要从中选择一名成绩好且发挥稳定的运动员参加比赛，应选择（）

A、甲 B、乙 C、丙 D、丁

查看试题解析

9. 数学老师计算同学们一学期的总评成绩时，将平时、期中和期末的成绩按2：3：5计算，若小红平时、期中和期末的成绩分别是90分、80分、96分，则小红一学期的数学总评成绩是（）

A、90分 B、91分 C、92分 D、93分

查看试题解析
10. 已知 $x_{1}$ 、 $x_{2}$ 、 $x_{3}$ 、 $x_{4}$ 、 $x_{5}$ 是按从小到大顺序排列的5个连续整数，若将这组数据变为 $x_{1} + 1$ 、 $x_{2} + 1$ 、 $x_{3}$ 、 $x_{4} - 1$ 、 $x_{5} - 1$ ，则这组新数据与原来相比（）

A、平均数变大 B、中位数变小 C、极差变大 D、方差变小

查看试题解析

二、填空题（每空3分，共15分）

11. 甲、乙两人在相同条件下进行射击练习，每人10次射击战绩的平均数都是8环，方差分别为 $s_{甲}^{2} = 1.4 ， s_{乙}^{2} = 0.6$ ，则两人射击成绩比较稳定的是（填“甲”或“乙”）.

查看试题解析
12. 某鞋厂调查了商场一个月内不同尺码运动鞋的销量，在平均数、中位数、众数这三个统计量中，该鞋厂最关注的是.

查看试题解析
13. 某同学在篮球场练习罚球线投篮，每轮投10次，5轮练习后命中的次数分别为4，x，9，8，2，若这组数据的中位数为7，则这组数据的平均数为．

查看试题解析
14. 我市测得一周 $P M_{2.5}$ 的日均值 $($ 单位：微克 $/$ 立方米 $)$ 如下： $50$ ， $40$ ， $75$ ， $50$ ， $37$ ， $50$ ， $40$ ，这组数据的中位数和众数分别是．

查看试题解析
15. 一次演讲比赛中，评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分．各项成绩均按百分制计，然后再按演讲内容占50%，演讲能力占40%、演讲效果占10%，计算选手的综合成绩（百分制）．进入决赛的前两名选手的单项成绩如表所示，则获得第一名的选手为．
选手
演讲内容
演讲能力
演讲效果
小明
90
80
90
小红
80
90
90

查看试题解析

三、解答题（共8题，共75分）

16. 在全运会射击比赛的选拔赛中，运动员甲10次射击成绩的统计表和扇形统计图如下：
命中环数
10
9
8
7
命中次数
▲
3
2
▲

(1)、根据统计表(图)中提供的信息，补全统计表及扇形统计图；

(2)、已知乙运动员10次射击的平均成绩为9环，方差为1.2，如果只能选一人参加比赛，你认为应该派谁去？并说明理由.

查看试题解析
17. 2022年末，中国迎来第一波疫情高峰．为加强同学们的防护意识，某校举行了以“疫情防护”为主题的知识竞赛活动．发现该校全体学生的竞赛成绩（百分制）均不低于60分，现从中随机抽取n名学生的竞赛成绩进行整理和分析（成绩得分用x表示，共分成四组），并绘制成如下的竞赛成绩分组统计表和扇形统计图，下面为部分数据：其中“ $80 \leq x < 90$ ”这组的部分数据（从小到大排序）如下：80，82，82，83，83，84，85，85，85，86，87，87，87，88，88……其中“ $90 \leq x \leq 100$ ”这组的数据如下：90，92，93，95，95，96，96，96，97，100．
竞赛成绩分组统计表
组别
竞赛成绩分组
频数
平均分
1
$60 \leq x < 70$
8
65
2
$70 \leq x < 80$
a
75
3
$80 \leq x < 90$
b
88
4
$90 \leq x \leq 100$
10
95
根据以上信息，回答下列问题：

(1)、下列说法正确的是____．

A、样本为n名学生 B、a＝12 C、m＝40

(2)、“ $90 \leq x \leq 100$ ”这组的数据的众数是．

(3)、随机抽取的这n名学生竞赛成绩的中位数是；平均分是；

(4)、若学生竞赛成绩达到96分以上（含96分）获奖，请你估计全校1200名学生中获奖的人数．

查看试题解析
18. 为了进一步了解某校初中学生的体质健康状况，对九年级的部分学生进行了体质抽测.同时统计了每个人的得分.体质抽测的成绩分为四个等级：优秀 $(45 \leq x \leq 50)$ 、良好 $(40 \leq x < 45)$ 、合格 $(30 \leq x < 40)$ ，不合格 $(0 \leq x < 30)$ 根据调查结果绘制了下列两福不完整的统计图，请你根据统计图提供的信息回答以下问题：

(1)、补全上面的扇形统计图和条形统计图；

(2)、被测试的部分九年级学生的体质测试成绩的中位数落在等级；

(3)、若该校九年级有1200名学生，估计该校九年级体质为“不合格”的学生约有多少人？

查看试题解析

19. 为了从甲、乙两位同学中选拔一人参加知识竞赛，举行了6次选拔赛，根据两位同学6次选拔赛的成绩，分别绘制了如图统计图.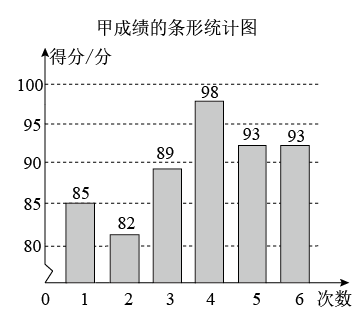

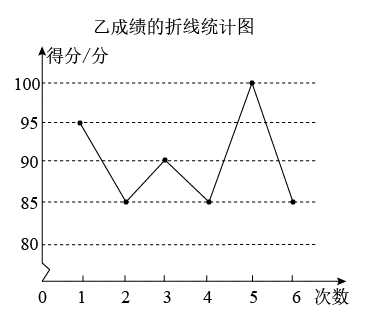(1)、填写下列表格

	平均数/分	中位数/分	众数/分
甲	90	①	93
乙	②	87.5	③

(2)、已求得甲同学6次成绩的方差为

\frac{133}{6}

（分²），求出乙同学6次成绩的方差；

(3)、你认为选择哪一位同学参加知识竞赛比较好？请说明理由.

查看试题解析

20. 2022年10月12日，“天宫课堂”第三课在中国空间站开讲，学校对七年级500名学生进行了一次航空航天知识竞赛，并随机抽取甲、乙两个班各50名学生的测试成绩（成绩均为整数，满分50分，但两班均无满分）进行整理、描述和分析.下面给出了部分信息.（用x表示成绩：A：30≤x＜34，B：34≤x＜38，C：38≤x＜42，D：42≤x＜46，E：46≤x＜50）

乙班成绩在D组的具体分数是：

42，42，42，42，42，42，42，42，42，42，43，44，45，45.

班级	甲班	乙班
平均分	44.1	44.1
中位数	44.5	n
众数	m	42
方差	7.7	17.4

根据以上信息，回答下列问题：

(1)、直接写出m，n的值，m＝， n＝.

(2)、悠悠这次测试成绩是44分，在班上排名属中游略偏上，悠悠是甲、乙哪个班级学生？说明理由；

(3)、假设该校七年级学生都参加此次测试，成绩达到45分及45分以上为优秀，估计该校本次测试成绩优秀的学生人数.

查看试题解析

21. 七中育才学校排球活动月即将开始，其中有一项为垫球比赛，体育组为了了解七年级学生的训练情况，随机抽取了七年级部分学生进行1分钟垫球测试，并将这些学生的测试成绩（即1分钟的个数，且这些测试成绩都在60～180范围内）分段后给出相应等级，具体为：测试成绩在60～90范围内的记为D级，90～120范围内的记为C级，120～150范围内的记为B级，150～180范围内的记为A级.现将数据整理绘制成如下两幅不完整的统计图，其中在扇形统计图中A级对应的圆心角为90°，请根据图中的信息解答下列问题：

(1)、在扇形统计图中，A级所占百分比为；

(2)、在这次测试中，一共抽取了 ▲ 名学生，并补全频数分布直方图；

(3)、在（2）中的基础上，在扇形统计图中，求D级对应的圆心角的度数；

(4)、若A，B，C，D等级的平均成绩分别为165、135、105、75个，你能估算出学校七年级同学的平均水平吗？若能，请计算出来.（保留准确值）

查看试题解析
22. 钟南山院士谈到防护新型冠状病毒肺炎时说：“我们需要重视防护，但也不必恐慌，尽量少去人员密集的场所，出门戴口罩，在室内注意通风，勤洗手，多运动，少熬夜.”湘潭市某学校为了加强学生对新型冠状病毒肺炎防护知识的了解，在七年级的学生中进行了一次《新型冠状病毒防治知识问答》（满分100分），学校从七年级中随机抽取各20名学生的成绩，并对他们的成绩（单位：分）进行统计分析，过程如下：
收集数据：
七年级：80 85 100 90 95 95 75 65 85 85
70 100 90 80 90 90 95 80 75 90
整理数据：
年级
成绩x（分）分
$60 \leq x \leq 70$
$70 < x \leq 80$
$80 < x \leq 90$
$90 < x \leq 100$
七年级
2
a
8
5
分析数据：
年级
统计量
平均数
中位数
众数
数据
85.75
87.5
b
应用数据：

(1)、填空： $a =$ ， $b =$ ；

(2)、补全频数分布直方图.

(3)、若七年级共有1200人参与答题，请估计七年级成绩 $70 < x \leq 90$ 的人数.

查看试题解析
23. 某校举行“中国共产党十九大”知识问答竞赛.每班选20名同学参加比赛.根据答对的题目数量得分，等级分为5分，4分，3分，2分.学校将八年级甲班和乙班的成绩整理并绘制成如下的统计图.
甲班知识问答成绩统计图乙班知识问答成绩统计图
甲、乙两班成绩统计表
班级
平均数（分）
中位数（分）
众数（分）
甲班
a
4
4
乙班
3.6
3.5
b

(1)、请把甲班知识问答成绩统计图补充完整.

(2)、通过统计得到上表，请求出表中数据a，b的值.

(3)、根据（2）的结果，你认为甲，乙两班哪个班级成绩更好？写出你的理由.

查看试题解析

选手	演讲内容	演讲能力	演讲效果
小明	90	80	90
小红	80	90	90

组别	竞赛成绩分组	频数	平均分
1	$60 \leq x < 70$	8	65
2	$70 \leq x < 80$	a	75
3	$80 \leq x < 90$	b	88
4	$90 \leq x \leq 100$	10	95

班级	平均数（分）	中位数（分）	众数（分）
甲班	a	4	4
乙班	3.6	3.5	b

册数	0	1	2	3	4
人数	3	13	16	17	1

命中环数	10	9	8	7
命中次数	▲	3	2	▲