北师大版2022-2023学年度第二学期七年级数学 平行线的性质 期中复习
试卷更新日期：2023-04-14 类型：复习试卷
一、单选题
-
1. 如图，直线 ， 直线 ， 若 ， 则的度数为（ ）
A、50° B、45° C、40° D、30°2. 如图，将一副三角板按如图放置，则下列结论：①∠1=∠3，②如果∠2=30°时，则有ACDE，③如果∠2=30°，必有∠4=45°，④如果∠2=30°，则AB⊥DE．其中正确的有（ ）
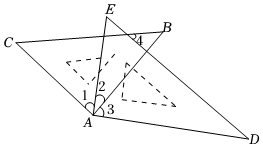A、①②③ B、②③④ C、①②④ D、①②③④3. 如图，AB∥CD， ， ， 则的度数是（ ）
A、30° B、40° C、50° D、45°4. 如图，已知直线AB，CD被直线AC所截， ， E是平面内任意一点（点E不在直线AB，CD，AC上），设∠BAE＝α，∠DCE＝β，下列各式：①β﹣α，②α﹣β，③180°﹣α+β，④360°﹣α﹣β，可以表示∠AEC的度数的有（ ）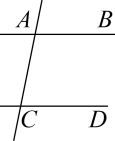
A、③④ B、①③④ C、①②④ D、②③④5. 如图，在四边形中，下列结论正确的是（ ）
A、若 ， 则 B、若 ， 则 C、若 ， 则 D、若 ， 则6. 如图，直线a∥b，直线c与直线a，b分别交于点A，B，AD⊥b于点D，若∠1=57°，则∠2的度数为（ ）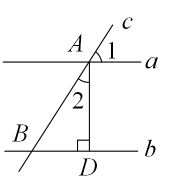
A、30° B、32° C、33° D、40°7. 如图，直线 ， 直线与直线 ， 分别交于点、 ， 射线直线 ， 则图中与互余的角有（ ）
A、1个 B、2个 C、3个 D、4个8. 如图，在三角形ABC中，点D，E，F分别在AB，AC，BC上， ， ， 则下列结论错误的是（ ）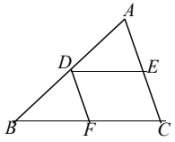
A、 B、 C、 D、9. 如图，弯形管道ABCD的拐角∠ABC＝120°，要保证管道 ， 则∠BCD等于（ ）
A、60° B、50° C、70° D、65°10. 如图，直线 ， 直线c与a ， b分别交于A ， B两点，若∠1=50°，则∠2的度数是（ ）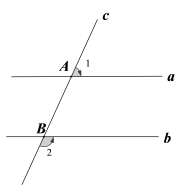
A、50° B、130° C、140° D、150°二、填空题
-
11. 已知：如图，在中， ， 过点且平行于 ， 若 ， 则的度数为 ．
12. 如图，已知直线、被直线所截，且∥ ， ∠1=°，那么∠2 =度；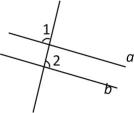
13. a、b、c是直线，且a∥b，b⊥c，则a与c的位置关系是 ．14. 如图，已知直线ab，cd，若∠1、∠2是图中的两个角，且这两个角的两边分别平行， ， ， 则x值为 ．
15. 将一副三角板按如图放置，有下列结论：①若 ， 则；②若 ， 则；③；④若 ， 则 ． 其中正确的是 ． （填序号）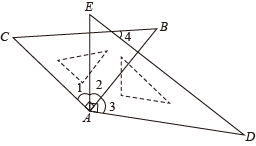
三、解答题
-
16. 如图，EF∥AD，∠DGA+∠BAC＝180°，说明：∠1＝∠2，请将说明过程填写完成.
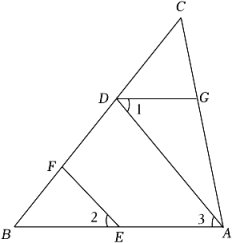
解：∵EF∥AD，（已知）
∴∠2＝▲ .（ ）
∵∠DGA+∠BAC＝180°，（ ）
∴DG∥AB，（ ）
∴∠1＝∠3，（ ）
∴∠1＝∠2.（ ）
17. 已知：如图，∠B＋∠3＝90°，∠B＋∠E＝90°，∠1＝∠E，求证：AD平分∠BAC，请完善证明过程，并在括号内填上相应依据：
证明：∵∠B＋∠3＝90°，∠B＋∠E＝90°，（ ）
∴▲ ＝▲ ， （ ）
∴ ， （ ）
∴∠2＝∠1，（ ）
∵∠E＝∠1（已知），
∴▲ ＝▲ ， （ ）
∴AD平分∠BAC．（ ）
18. 请把下列的证明过程补充完整：已知：如图，∠1+∠2＝180°，∠A＝∠D，求证：AB∥CD，
证明：∵∠1与∠CGD是对顶角，
∴∠1＝∠CGD（ ）．
又∵∠1+∠2＝180°（已知）．
∴∠CGD+∠2＝180°，
∴AE∥FD（ ），
∴∠A＝∠BFD（ ）．
∵∠A＝∠D（已知），
∴∠BFD＝∠D（ ），
∴AB∥CD（ ）．
四、综合题
-
19. 已知：如图，和上的一点P.
(1)、求作直线 ， 使直线过点P且；(2)、写出一对相等的同位角和一对互补的同旁内角.20. 如图，直线ABCD，直线与、分别交于点、 ， 小安将一个含角的直角三角板按如图①放置，使点、分别在直线、上，且在点、的右侧， ， ．
(1)、填空：（填“”“”或“”）；(2)、若的平分线交直线于点 ， 如图②．①当ONEF，PMEF时，求的度数；
②小安将三角板保持PMEF并向左平移，在平移的过程中求的度数（用含的式子表示）．
21. 如图1，点E、F分别在直线AB、CD上，点P为AB、CD之间的一点，且 ．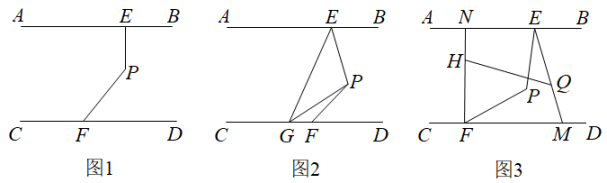
(1)、求证：；(2)、如图2，点G在射线FC上，PG平分 ， ， 探究与之间的数量关系．并说明理由；(3)、如图3， ， ． 直线HQ分别交FN，EM于H、Q两点，若 ， 求的度数．22. 如图， ， 点O是上一点，直线经过点O，且平分 ， 过点A作于点A，且；
(1)、求的度数；(2)、连接 ， 若 ， 求的度数．23. 已知：如图，直线 ， 点C是PQ，MN之间（不在直线PQ，MN上）的一个动点.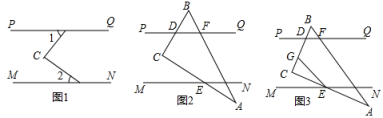
(1)、若∠1与∠2都是锐角，如图1，请直接写出∠C与∠1∠2之间的数量关系.(2)、若小明把一块三角板（∠A=30°，∠C=90°）如图2放置，点D，E，F是三角板的边与平行线的交点，若∠AEN=∠A，求∠BDF的度数.(3)、将图2中的三角板进行适当转动，如图3，直角顶点C始终在两条平行线之间，点G在线段CD上，连结EG，且有∠CEG=∠CEM，给出下列两个结论：①的值不变；
②∠GEN－∠BDF的值不变.
其中只有一个是正确的，你认为哪个是正确的？讲求出不变的值是多少.