北师大版2022-2023学年度第二学期七年级数学 两条直线的位置关系 期中复习
试卷更新日期：2023-04-14 类型：复习试卷
一、单选题
-
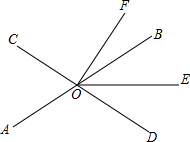
1. 如图，直线、、相交于点 ， 其中 ， ：： ， 则（ ）
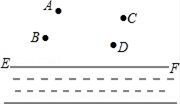
A、 B、 C、 D、2. 如图，要把河中的水引到水池A中，应在河岸B处（AB⊥CD）开始挖渠才能使水渠的长度最短，这样做依据的几何学原理是（ ）
A、垂线段最短 B、点到直线的距离 C、两点确定一条直线 D、两点之间线段最短3. 下面四个图形中，与是对顶角的是（ ）A、
B、
C、
D、
4. 平面上不重合的两点确定1条直线，不同三点最多可确定3条直线.若平面上5条直线两两相交，交点最多有a个，最少有b个，则（ ）A、8 B、9 C、10 D、115. 下列结论：①多个有理数相乘，负因数的个数为奇数时积为负；②若 ， 则；③若 ， 且 ， 则的余角为；④若、为常数，无论取何值，关于的方程的解恒为 ， 则 ， ， 其中正确结论的个数有（ ）A、1个 B、2个 C、3个 D、4个6. 下列各图中，和是对顶角的是（ ）A、
B、
C、
D、
7. 如图，直线AB，CD相交于点O， ， OF平分 ， 则的大小为（ ）
A、40° B、50° C、65° D、70°8. 如图，小明手持手电筒照向地面，手电筒发出的光线CO与地面AB形成了两个角，∠BOC＝8∠AOC ， 则∠BOC的度数是（ ）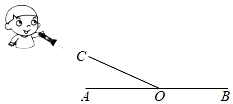
A、160° B、150° C、120° D、20°9. 若 ， 则的对顶角的大小为（ ）A、40° B、50° C、130° D、140°10. 在同一平面内，不重合的两条直线可能的位置关系是（ ）A、平行 B、相交 C、平行或相交 D、不能确定二、填空题
-
11. 如图，已知直线与交于点 ， 平分 ， 若 ， 则 的度数为 ．
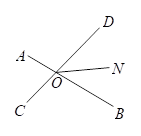12. 如果∠A＝60°，那么∠A的邻补角等于 ．13. 已知 ， 则的余角为.14. 如图，OC⊥OD，∠1＝35°，则∠2＝ ．
15. 如图，与是对顶角， ， ， 则°．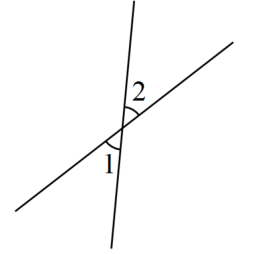
三、解答题
-
16. 如图，AO⊥CO，BO⊥DO，∠BOC=43°，求∠AOD和∠AOB的度数.
17. 如图，直线AB和CD相交于点O，若 ， OA平分 ， 求的度数．
18. 如图，直线EF和CD相交于点O，射线 ， 且OC平分∠AOF，∠BOD＝20°．求∠BOE的度数．
四、综合题
-
19. 如图，直线、相交于点 ， 且平分 ， 平分 .
(1)、求证：平分；(2)、求的度数.20. 如图，直线AB，CD相交于点O，∠AOD＝2∠BOD＋60°.
(1)、求∠BOD的度数；(2)、以O为端点引射线OE，OF，射线OE平分∠BOD，且∠EOF＝90°，求∠BOF的度数.21. 如图，直线EF、CD相交于点O，OA⊥OB，OC平分∠AOF．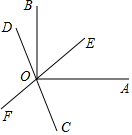
(1)、直接写出∠DOF的对顶角和邻补角；(2)、若∠AOE＝30°，求∠BOD的度数．
