北师大版2022-2023学年度第二学期七年级数学完全平方公式期中复习

试卷更新日期：2023-04-14 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 ${(- 2 x^{3})}^{2} = 4 x^{6}$ B、 $x^{2} + x^{3} = x^{5}$ C、 $x^{8} \div x^{2} = x^{4}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
2. 若 $x + y = - 2$ ， $x^{2} + y^{2} = 10$ ，则 $x y =$ （）

A、-3 B、3 C、-4 D、4

查看试题解析
3. 下列多项式能用完全平方公式进行因式分解的是（）

A、 $a^{2} - 2 a + 4$ B、 $a^{2} + 2 a - 1$ C、 $a^{2} + a - 1$ D、 $a^{2} - 4 a + 4$

查看试题解析
4. 在多项式 $16 x^{2} + 1$ 添加一个单项式，使得到的多项式能运用完全平方公式分解因式，则下列表述正确的是（）
嘉琪：添加 $\pm 8 x$ ， $16 x^{2} + 1 \pm 8 x = {(4 x \pm 1)}^{2}$
陌陌：添加 $64 x^{4}$ ， $64 x^{4} + 16 x^{2} + 1 = {(8 x^{2} + 1)}^{2}$
嘟嘟：添加 $- 1$ ， $16 x^{2} + 1 - 1 = 16 x^{2} = {(4 x)}^{2}$

A、嘉琪和陌陌的做法正确 B、嘉琪和嘟嘟的做法正确 C、陌陌和嘟嘟的做法正确 D、三位同学的做法都错误

查看试题解析
5. 如图所示、有三种卡片，其中边长为a的正方形卡片有1张，长为a，宽为b的矩形卡片有4张，边长为b的正方形卡片有4张，用这9张卡片刚好供成一个大正方形，则这个大正方形的边长为（　　）

A、a+2b B、2a+2b C、2a+b D、a+b

查看试题解析
6. 如图所示分割正方形，各图形面积之间的关系验证了一个等式，这个等式是（）

A、 ${(y + x)}^{2} = y^{2} + 2 x y + x^{2}$ B、 ${(y - x)}^{2} = y^{2} - 2 x y + x^{2}$ C、 $(y - x) (y + x) = y^{2} - x^{2}$ D、 ${(y + x)}^{2} - {(y - x)}^{2} = 4 x y$

查看试题解析
7. 已知 ${(3 x + a)}^{2} = 9 x^{2} + b x + 4$ ，则b的值为（）

A、4 B、 $\pm 6$ C、12 D、 $\pm 12$

查看试题解析
8. 若多项式 $4 - a x + x^{2}$ 可以分解因式为 ${(2 - x)}^{2}$ ，则a的值是（）

A、 $2$ B、 $- 2$ C、 $4$ D、 $\pm 4$

查看试题解析
9. 将 $9 7^{2}$ 变形正确的是（）

A、 $9 7^{2} = 9 0^{2} + 7^{2}$ B、 $9 7^{2} = (100 + 3) (100 - 3)$ C、 $9 7^{2} = 10 0^{2} - 2 \times 100 \times 3 + 3^{2}$ D、 $9 7^{2} = 9 0^{2} + 90 \times 7 + 7^{2}$

查看试题解析
10. 在数学活动课上，一位同学用四张完全一样的长方形纸片（长为 $a$ ，宽为 $b$ ， $a > b$ ）搭成如图一个大正方形，面积为132，中间空缺的小正方形的面积为28.下列结论中，正确的有（）.

① ${(a - b)}^{2} = 28$ ；② $a b = 26$ ；③ $a^{2} + b^{2} = 80$ ；④ $a^{2} - b^{2} = 64$

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题

11. 计算： $29 5^{2} + 10 \times 295 + 5^{2} =$

查看试题解析
12. 已知 $a - b = b - c = \frac{3}{5} ， a^{2} + b^{2} + c^{2} = 1$ ，则 $a b + b c + c a$ 的值等于．

查看试题解析
13. 如图，有三种卡片，其中边长为a的正方形卡片1张，边长分别为a、b的矩形卡片6张，边长为b的正方形卡片9张．用这16张卡片拼成一个正方形，则这个正方形的边长为．

查看试题解析
14. 已知 $a b = 12 ， a^{2} + b^{2} = 25 ，则 {(a + b)}^{2} =$ ．

查看试题解析
15. 已知（2021-a）（a-2022）＝5，则（a-2021）²+（a-2022）²＝．

查看试题解析

三、解答题

16. 如果 ${(x^{3} - 3 a + \frac{1}{x^{3}})}^{2} + {(x + 2 b + \frac{1}{x})}^{2} = 0$ ，求 $3 a + 2 b (4 b^{2} - 3)$ 的值．

查看试题解析
17. 已知 $a^{2} + b^{2} + c^{2} = 20$ ， $a b + a c + b c = 8$ ，求 $(a + b + c)^{2}$ 的值．

查看试题解析
18. 先化简，再求值： $(2 x + 5) (2 x - 5) + {(x - 3)}^{2} - 6 x (x - 1)$ ，其中 $x = 6$ .

查看试题解析

四、综合题

19.

(1)、已知x＋y＝3，xy＝2．求 $x^{2} + y^{2}$ 、 ${(x - y)}^{2}$ 的值；

(2)、已知x＋2y＝3，xy＝1．求 $x^{2} - x y + 4 y^{2}$ 的值．

查看试题解析
20. 在数学中，有许多关系都是在不经意间被发现的，请认真观察图形，解答下列问题：

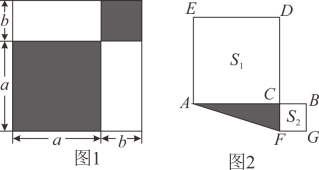(1)、如图1，用两种不同的方法表示阴影图形的面积，得到一个等量关系：．

(2)、若图1中a、b满足a+b＝7，ab＝10，求a²+b²的值；

(3)、如图2，C是线段AB上一点，以AC，BC为边向两边作正方形，AC+BC=8，两正方形面积和S₁+S₂＝40，求图中阴影部分面积．

查看试题解析
21. 图①是一个长为 $m$ ，宽为 $4 n$ （ $m > n$ ）的长方形，用剪刀沿图中虚线剪开，把它平均分成形状和大小都一样的四个小长方形，然后按图②那样拼成一个正方形．

(1)、观察图②，可得： ${(m + n)}^{2} - {(m - n)}^{2} =$ ；

(2)、若 $m - n = 7$ ， $m n = 6$ ，求 ${(m + n)}^{2}$ 的值；

(3)、当 $(x - 10) (20 - x) = 8$ 时，求 ${(2 x - 30)}^{2}$ 的值．

查看试题解析
22. 如图

(1)、数学中有很多等式可以用图形的面积来表示.观察上图，直接写出代数式（a+b）² ，（a-b）² ， ab之间的等量关系；

(2)、根据（1）题中的等量关系，解决如下问题：
①已知m-n = 7，mn=-12.求m+n的值；

②若（6-x）（8+x） = 7，求（6-x）²+（8+x）²的值.

查看试题解析
23. 【阅读材料】
我们知道，图形也是一种重要的数学语言，它直观形象，能有效地表现一些代数中的数关系，而运用代数思想也能巧妙地解决一些图形问题．
在一次数学活动课上，张老师准备了若干张如图1所示的甲、乙、丙三种纸片，其中甲种纸片是边长为x的正方形，乙种纸片是边长为y的正方形，丙种纸片是长为y，宽为x的长方形，并用甲种纸片一张，乙种纸片一张，丙种纸片两张拼成了如图2所示的一个大正方形．

(1)、【理解应用】
观察图2，用两种不同方式表示阴影部分的面积可得到一个等式，请你直接写出这个等式；

(2)、【拓展升华】
利用（1）中的等式解决下列问题
①已知 $a^{2} + b^{2} = 20$ ， $a + b = 6$ ，求ab的值；
②已知 $(2021 - c) (c - 2019) = 1$ ，求 ${(2021 - c)}^{2} + {(c - 2019)}^{2}$ 的值．

查看试题解析

北师大版2022-2023学年度第二学期七年级数学 完全平方公式 期中复习

一、单选题

二、填空题

三、解答题

四、综合题

北师大版2022-2023学年度第二学期七年级数学完全平方公式期中复习