北师大版2022-2023学年度第二学期七年级数学整式的乘法期中复习

试卷更新日期：2023-04-14 类型：复习试卷

进入出卷网下载

一、单选题

1. 若 $(x + m) (x^{2} + n x + 1)$ 的展开式中常数项为-2，且不含 $x^{2}$ 项，则展开式中一次项的系数为（）

A、-2 B、2 C、3 D、-3

查看试题解析
2. 长方形一边长为 $2 a + b ，$ 另一边比它小 $a - b$ 则长方形面积为（）

A、 $2 a^{2} + a b - b^{2}$ B、 $2 a^{2} + a b$ C、 $4 a^{2} + 4 a b + b^{2}$ D、 $2 a^{2} + 5 a b + 2 b^{2}$

查看试题解析
3. 若x+m与x﹣5的乘积中不含x的一次项，则m的值是（）

A、﹣5 B、0 C、1 D、5

查看试题解析
4. 已知 $a_{1} ， a_{2} ， \dots ， a_{2020}$ 都是正数，如果（） $M = (a_{1} + a_{2} + \dots + a_{2019}) (a_{2} + a_{3} + \dots + a_{2020}) ， N = (a_{1} + a_{2} + \dots +$ $a_{2020}) (a_{2} + a_{3} + \dots + a_{2019})$ ，那么 $M 、 N$ 的大小关系是（）

A、 $M > N$ B、 $M = N$ C、 $M < N$ D、不确定

查看试题解析
5. 若 $(x + 3) (x - 5) = x^{2} + m x - 15$ ，则 $m$ 的值为（）

A、2 B、-2 C、5 D、-5

查看试题解析
6. 若x²-bx-10=（x+5）（x-a），则a^b的值是（）

A、-8 B、8 C、 $\frac{1}{8}$ D、 $- \frac{1}{8}$

查看试题解析
7. 如图所示的正方形和长方形卡片各有若干张，若要拼成一个长为 $(a + 2 b)$ ，宽为 $(2 a + b)$ 的长方形，则需要 $A$ 类， $B$ 类， $C$ 类卡片各（）张.

A、2，3，2 B、2，4，2 C、2，5，2 D、2，5，4

查看试题解析
8. 若 $(x - 3) (x^{2} + a x + b)$ 的积中不含x的二次项和一次项，则a和b的值（）

A、a＝0；b＝2 B、a＝3；b＝9 C、a＝－1；b＝2 D、a＝2；b＝4

查看试题解析
9. 若 $x^{2} + m x + n$ 分解因式的结果是 $(x - 2) (x + 1)$ ，则 $m + n$ 的值为（）

A、-3 B、3 C、1 D、-1

查看试题解析
10. 如图，正方形卡片A类，B类和长方形卡片C类若干张，要拼一个长为（a+mb），宽为（3a+b）的大长方形（m为常数），若知道需用到的B类卡片比A类卡片少1张，则共需C类卡片（）张.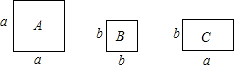

A、5 B、6 C、7 D、8

查看试题解析

二、填空题

11. 计算 $3 x \cdot 2 x^{2} y$ 的结果是．

查看试题解析
12. 已知二次三项式x²+px+q因式分解的结果是（x﹣3）（x﹣5），则（2p+q）²⁰²⁰ ．

查看试题解析
13. 若（x－2）（x＋m）＝x²＋3x＋n，则m－n＝．

查看试题解析
14. 计算 $- 3 a \cdot (2 b)$ ＝．

查看试题解析
15. 某同学在计算多项式A乘 $2 x^{2}$ 时，因抄错运算符号，算成了加 $2 x^{2}$ ，得到的结果是 $x^{2} - 4 x + 1$ ，那么正确的计算结果是.

查看试题解析

三、解答题

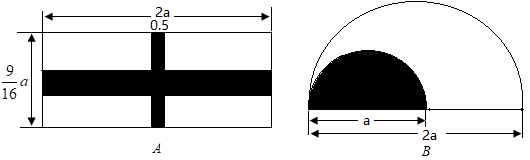
16. 已知多项式（2x+1）（x²+ax+2）的结果中不含有x²项（a是常数），求代数式a²+a+ $\frac{1}{4}$ 的值.

查看试题解析
17. 甲乙两人共同做一道整式乘法的计算题(2x+a)(3x+b)，由于甲抄错了第1个多项式中a的符号，得到的结果为6x²+7x+2，由于乙漏抄了第2个多项式中x的系数，得到的结果为2x²+3x-2，请你计算出a、b的值各是多少，并写出正确的算式及结果。

查看试题解析
18. 如图，公园里有A、B两个花坛，A花坛是长为20米，宽为 $\frac{9}{16} a$ 米的长方形，花坛中间16横竖各铺设一条小路（阴影部分），竖着的小路宽为0.5米，横着的小路宽为1米，剩余部分栽种花卉；B花坛是直径为 $2 a$ 米的半圆，其中修建一个半圆形水池（阴影部分），剩余部分栽种花卉，求B花坛比A花坛栽种花卉的面积大多少？（取 $π$ ）

查看试题解析

四、综合题

19. 我们知道，根据几何图形的面积关系可以说明一些等式的成立．
例如： $(x + a) (x + b) = x^{2} + (a + b) x + a b$ 可以用图1的面积关系来说明．

(1)、根据图2写出一个等式；

(2)、请你再举一个例子，写出等式并在图3空白处画出一个相应的几何图形加以说明（注：不必证明，用代数式标出各部分面积即可）．

查看试题解析
20. 如图，长为40，宽为 $x$ 的大长方形被分割为9小块，除阴影 $A$ ， $B$ 两个长方形外，其余7块是形状、大小完全相同的小长方形，其较短一边长为 $y$ ．

(1)、分别用含 $x$ ， $y$ 的代数式表示阴影 $A$ ， $B$ 两个长方形的长和宽；

(2)、分别用含 $x$ ， $y$ 的代数式表示阴影 $A$ ， $B$ 两个长方形的面积．

查看试题解析
21. 一个长方形的长为2x cm，宽比长少4cm，若将长方形的长和宽都扩大3cm．

(1)、求面积增大了多少？

(2)、若x=2cm，则增大的面积为多少？

查看试题解析
22. 你能化简（a﹣1）（a⁹⁹+a⁹⁸+a⁹⁷+…+a²+a+1）吗？
我们不妨先从简单情况入手，发现规律，归纳结论．

(1)、先填空：（a﹣1）（a+1）=；（a﹣1）（a²+a+1）=；（a﹣1）（a³+a²+a+1）=；
由此猜想：（a﹣1）（a⁹⁹+a⁹⁸+a⁹⁷+…+a²+a+1）=

(2)、利用这个结论，你能解决下面两个问题吗？
①求 2¹⁹⁹+2¹⁹⁸+2¹⁹⁷+…+2²+2+1 的值；
②若 a⁵+a⁴+a³+a²+a+1=0，则a⁶等于多少？

查看试题解析
23. 如图，甲长方形的长为m+7，宽为m+1，面积为S₁；乙长方形的长为m+4，宽为m+2，面积为S₂ ．（m为正整数）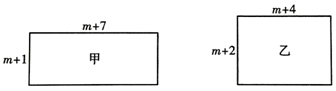

(1)、试比较S₁ ， S₂的大小；

(2)、现有一正方形，其周长与图中的甲长方形周长相等，试探究：该正方形面积S与图中的甲长方形面积S₁的差（即S﹣S₁）是一个常数，求出这个常数．

查看试题解析

北师大版2022-2023学年度第二学期七年级数学 整式的乘法 期中复习

一、单选题

二、填空题

三、解答题

四、综合题

北师大版2022-2023学年度第二学期七年级数学整式的乘法期中复习