2023年沪科版数学八年级下册期中测试模拟卷(一)
试卷更新日期:2023-04-14 类型:期中考试
一、单选题(每题4分,共40分)
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 下列各式运算正确的是( )A、 B、 C、 D、3. 下列图形中,内角和与外角和相等的多边形是( )A、
 B、
B、 C、
C、 D、
D、 4. 估计 的值在( )A、0到l之间 B、1到2之间 C、2到3之间 D、3到4之间5. 下列二次根式中,与是同类二次根式的是( )A、 B、 C、 D、6. 如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形的四条边为边向外作四个正方形,若S1+S4=135,S3=49,则S2=( )
4. 估计 的值在( )A、0到l之间 B、1到2之间 C、2到3之间 D、3到4之间5. 下列二次根式中,与是同类二次根式的是( )A、 B、 C、 D、6. 如图,在四边形ABCD中,∠DAB=∠BCD=90°,分别以四边形的四条边为边向外作四个正方形,若S1+S4=135,S3=49,则S2=( ) A、184 B、86 C、119 D、817. 汽车产业的发展,有效促进了我国现代化建设.某汽车销售公司2018年盈利1000万元,2020年盈利1440万元,且从2018年到2020年,每年盈利的年增长率相同.设每年盈利的年增长率为x,则列方程得( )A、1000(1+2x)=1440 B、1000(1+x)2=1440 C、1000×2×(1+x)=1440 D、1000+1000(1+x)+1000(1+x)2=14408. 下列条件:① ;② ;③ ;④ ,能判定 是直角三角形的有( )A、4个 B、3个 C、2个 D、1个9. 已知 , 是关于的方程的两个根,则的值为( )A、2023 B、2022 C、2021 D、202010. 如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/秒,点Q的速度为2cm/秒,点Q移动到点C后停止,点P也随之停止运动.下列时间瞬间中,能使△PBQ的面积为15cm2的是( )
A、184 B、86 C、119 D、817. 汽车产业的发展,有效促进了我国现代化建设.某汽车销售公司2018年盈利1000万元,2020年盈利1440万元,且从2018年到2020年,每年盈利的年增长率相同.设每年盈利的年增长率为x,则列方程得( )A、1000(1+2x)=1440 B、1000(1+x)2=1440 C、1000×2×(1+x)=1440 D、1000+1000(1+x)+1000(1+x)2=14408. 下列条件:① ;② ;③ ;④ ,能判定 是直角三角形的有( )A、4个 B、3个 C、2个 D、1个9. 已知 , 是关于的方程的两个根,则的值为( )A、2023 B、2022 C、2021 D、202010. 如图,在△ABC中,∠ABC=90°,AB=8cm,BC=6cm.动点P,Q分别从点A,B同时开始移动,点P的速度为1cm/秒,点Q的速度为2cm/秒,点Q移动到点C后停止,点P也随之停止运动.下列时间瞬间中,能使△PBQ的面积为15cm2的是( ) A、2秒钟 B、3秒钟 C、3秒钟或5秒钟 D、5秒钟
A、2秒钟 B、3秒钟 C、3秒钟或5秒钟 D、5秒钟二、填空题(每题5分,共25分)
-
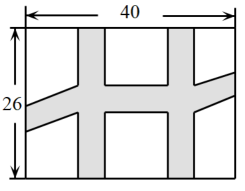
11. 计算: .12. 若直角三角形的两条直角边的长分别为5和 12,则斜边上的中线长为 .13. 已知是方程的根,则该方程的另一根为.14. 现要在一个长为 , 宽为的矩形花园中修建等宽的小道,剩余的地方种植花草.如图所示,要使种植花草的面积为 , 设小道的宽度应是 , 列方程得: .
 15. 已知是等腰直角三角形,且 , , 点D为AC的中点,动点E,F分别在AB,BC上运动,则周长的最小值为.
15. 已知是等腰直角三角形,且 , , 点D为AC的中点,动点E,F分别在AB,BC上运动,则周长的最小值为.
三、计算题(共2题,共20分)
-
16. 用适当的方法解下列方程(1)、;(2)、.17. 化简:(1)、(2)、
四、作图题(共10分)
-
18. 如图, .
 (1)、尺规作图:作的垂直平分线交于点D,交于点E(不写作法,保留作图痕迹);(2)、在(1)的基础上,连接 , 求的长.
(1)、尺规作图:作的垂直平分线交于点D,交于点E(不写作法,保留作图痕迹);(2)、在(1)的基础上,连接 , 求的长.五、解答题(共5题,共55分)
-
19. 阅读理解题,下面我们观察:
.反之所以所以.
完成下列各题:
(1)、把写成的形式;(2)、化简:;(3)、化简:.20. 已知:关于x的一元二次方程.(1)、判断方程的根的情况;(2)、若为等腰三角形, , 另外两条边长是该方程的根,求的周长.21. 如图所示,一架梯子AB斜靠在墙面上,且AB的长为2.5米. (1)、若梯子底端离墙角的距离OB为1.5米,求这个梯子的顶端A距地面有多高?(2)、在(1)的条件下,如果梯子的顶端A下滑0.5米到点A',那么梯子的底端B在水平方向滑动的距离BB'为多少米?22. 科学研究表明接种疫苗是战胜新冠病毒的最有效途径.当前居民接种疫苗迎来高峰期,导致相应医疗物资匮乏,某工厂及时补进了一条一次性注射器生产线生产一次性注射器.开工第一天生产200万个,第三天生产288万个.试回答下列问题:(1)、求前三天生产量的日平均增长率;(2)、经调查发现,1条生产线最大产能是600万个/天,若每增加 条生产线,每条生产线的最大产能将减少20万个/天.
(1)、若梯子底端离墙角的距离OB为1.5米,求这个梯子的顶端A距地面有多高?(2)、在(1)的条件下,如果梯子的顶端A下滑0.5米到点A',那么梯子的底端B在水平方向滑动的距离BB'为多少米?22. 科学研究表明接种疫苗是战胜新冠病毒的最有效途径.当前居民接种疫苗迎来高峰期,导致相应医疗物资匮乏,某工厂及时补进了一条一次性注射器生产线生产一次性注射器.开工第一天生产200万个,第三天生产288万个.试回答下列问题:(1)、求前三天生产量的日平均增长率;(2)、经调查发现,1条生产线最大产能是600万个/天,若每增加 条生产线,每条生产线的最大产能将减少20万个/天.①现该厂要保证每天生产一次性注射2600万个,在增加产能同时又要节省投入的条件下(生产线越多,投入越大),应该增加几条生产线?
②是否能增加生产线,使得每天生产一次性注射器5000万个,若能,应该增加几条生产线?若不能,请说明理由.
23. 如图,在中, , , , P、Q是边上的两个动点.其中点P从点A出发,沿方向运动,速度为每秒;点Q从点B出发,沿方向运动,速度为每秒;两点同时开始运动,设运动时间为秒.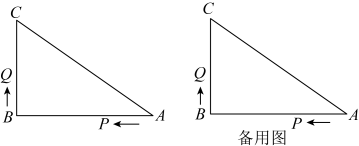 (1)、①斜边上的高为;
(1)、①斜边上的高为;②当时,的长为;
(2)、当点Q在边上运动时,出发几秒钟后,是等腰三角形?(3)、当点Q在边上运动时,直接写出所有能使成为等腰三角形的t的值.
-