广西南宁市2023届高三理数第一次适应性测试试卷

试卷更新日期：2023-04-13 类型：高考模拟

进入出卷网下载

一、单选题

1. 已知集合 $A = {x ∣ x > 4} ， B = {x \in Z ∣ 3 < x < 7}$ ，则 $A ∩ B =$ （）

A、 $(4 ， 6)$ B、 ${4 ， 7}$ C、 ${4 ， 5 ， 6 ， 7}$ D、 ${5 ， 6}$

查看试题解析
2. 已知复数 $z$ 满足 $\bar{z} (1 + i) = 3 - i$ （ $i$ 为虚数单位），则复数 $z =$ （）

A、 $1 + 2 i$ B、 $1 - 2 i$ C、 $1 + i$ D、 $1 - i$

查看试题解析
3. 电动工具已成为人们生产和生活中常备的作业工具､数据显示，全球电动工具零部件市场规模由2016年的58亿美元增长至2020年的72亿美元，复合年均增长率达5.55%，2022年全球电动工具零部件市场规模达到80亿美元.根据此图，下列说法中正确的是（）

A、2016-2022年全球电动工具零部件市场规模逐步减少 B、2016-2022年全球电动工具零部件市场规模增长速度逐年增长 C、2021年全球电动工具零部件市场规模大于2020年全球电动工具零部件市场规模 D、2018-2019年全球电动工具零部件市场规模增速的差值最大

查看试题解析
4. 已知 $s i n^{2} α = c o s α - 1$ ，则 $s i n (α + \frac{3 π}{2}) =$ （）

A、1 B、-1 C、2 D、 $- \frac{1}{2}$

查看试题解析
5. 已知数列 ${a_{n}}$ 满足 $a_{1} = \frac{1}{3} ， a_{n + 1} = \frac{a_{n}}{a_{n} + 1}$ ，则数列 ${\frac{1}{a_{n}}}$ 的前5项和为（）

A、25 B、26 C、32 D、 $\frac{1}{7}$

查看试题解析
6. 设随机变量 $X ∼ N (1 ， σ^{2})$ ， $P (1 < X < 2) = 0.28$ ，则 $P (X > 0) =$ （）

A、0.68 B、0.56 C、0.78 D、0.22

查看试题解析
7. 如图，已知圆锥的底面半径为1，母线长 $S A = 3$ ，一只蚂蚁从 $A$ 点出发绕着圆锥的侧面爬行一圈回到点 $A$ ，则蚂蚁爬行的最短距离为（）

A、 $2 \sqrt{3}$ B、 $3 \sqrt{3}$ C、6 D、 $2 π$

查看试题解析
8. 已知 $\sqrt{3} s i n α - s i n (α + \frac{π}{6}) = \frac{4}{5}$ ，则 $c o s (\frac{π}{3} - 2 α) =$ （）

A、 $- \frac{1}{25}$ B、 $- \frac{7}{25}$ C、 $\frac{24}{25}$ D、 $\frac{9}{25}$

查看试题解析
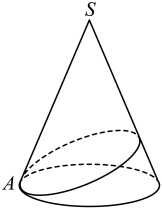9. 已知函数 $f (x) = x^{2}$ 的图象在 $x = 1$ 处的切线与函数 $g (x) = \frac{e^{x}}{a}$ 的图象相切，则实数 $a =$ （）

A、 $\sqrt{e}$ B、 $\frac{e \sqrt{e}}{2}$ C、 $\frac{\sqrt{e}}{2}$ D、 $e \sqrt{e}$

查看试题解析
10. 如图的形状出现在南宋数学家杨辉所著的《详解九章算法·商功》中，后人称为“三角垛”.“三角垛”的最上层有1个球，第二层有3个球，第三层有6个球……在2015年世乒赛期间，苏州某景点就用乒乓球堆成“三角垛”型的装饰品，假设一个“三角垛”装饰品共有n层，记使用的乒乓球数量为 $f (n)$ ，则 $f (n) =$ （）
（参考公式： $1^{2} + 2^{2} + 3^{2} + ⋯ + n^{2} = \frac{1}{6} n (n + 1) (2 n + 1)$ ）

A、 $\frac{1}{6} n (n + 1) (2 n + 1)$ B、 $\frac{n (n + 1)}{2}$ C、 $\frac{1}{3} n (n + 1) (n + 2)$ D、 $\frac{1}{6} n (n + 1) (n + 2)$

查看试题解析
11. 已知直线 $l ： y = k (x - \frac{p}{2})$ 与抛物线 $C ： y^{2} = 2 p x (p > 0)$ 相交于 $A$ 、 $､ B$ 两点（其中 $A$ 位于第一象限），若 $| B F | = 3 | F A |$ ，则 $k =$ （）

A、 $- \sqrt{3}$ B、 $- \frac{\sqrt{3}}{3}$ C、-1 D、 $- \frac{1}{3}$

查看试题解析
12. 已知函数 $f (x) = s i n (ω x + \frac{π}{3}) (ω > 0) ， f (x) = \frac{1}{2}$ 在区间 $[0 ， π]$ 上有且仅有2个零点，对于下列4个结论：①在区间 $(0 ， π)$ 上存在 $x_{1} ， x_{2}$ ，满足 $f (x_{1}) - f (x_{2}) = 2$ ；② $f (x)$ 在区间 $(0 ， π)$ 有且仅有1个最大值点；③ $f (x)$ 在区间 $(0 ， \frac{π}{15})$ 上单调递增；④ $ω$ 的取值范围是 $[\frac{11}{6} ， \frac{5}{2})$ ，其中所有正确结论的编号是

A、①③ B、①③④ C、②③ D、①④

查看试题解析

二、填空题

13. 若 $x ， y$ 满足约束条件 ${\begin{array}{l} x + y + 2 \leq 0 \\ 2 x - y + 2 \geq 0 \\ x \leq 2 \end{array}$ ，则 $z = 3 x + y$ 的最大值为．

查看试题解析
14. 如图，已知正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的棱长为 $2 ， E ､ F$ 分别是棱 $A A_{1} ， A_{1} D_{1}$ 的中点，点 $P$ 为底面四边形 $A B C D$ 内（包括边界）的一动点，若直线 $D_{1} P$ 与平面 $B E F$ 无公共点，则点 $P$ 在四边形 $A B C D$ 内运动所形成轨迹的长度为.

查看试题解析
15. 已知 $F_{1} ， F_{2}$ 是双曲线 $C$ 的两个焦点， $P$ 为 $C$ 上一点， $∠ F_{1} P F_{2} = 6 0^{∘}$ ，且 $s i n ∠ P F_{2} F_{1} = 2 s i n ∠ P F_{1} F_{2}$ ，则 $C$ 的离心率为．

查看试题解析
16. 已知函数 $f (x) = {\begin{array}{l} \frac{x}{e^{x + e}} - e^{2} ， x \leq 0 \\ - \sqrt{1 + x^{2}} ， x > 0 \end{array}$ ，点 $M ､ N$ 是函数 $y = f (x)$ 图象上不同的两个点，设 $O$ 为坐标原点，则 $t a n ∠ M O N$ 的取值范围是.

查看试题解析

三、解答题

17. 在 $△ A B C$ 中，角 $A ､ B ､ C$ 的对边分别为 $a ､ b ､ c$ ，已知 $(b - c) (s i n B + s i n C) = a (s i n A - s i n C)$ ，

(1)、求 $B$ ；

(2)、若 $△ A B C$ 为锐角三角形， $b = \sqrt{3}$ ，求 $a^{2} + c^{2}$ 的取值范围．

查看试题解析
18. 如图1，平面图形 $A B C D$ 是一个直角梯形，其中 $A B$ $∥$ $C D ， ∠ A B C = 9 0^{∘} ， B C = D C = 2 ， A B = 6$ ， $E$ 是 $A B$ 上一点，且 $A E = 2 E B$ .将 $△ A E D$ 沿着 $E D$ 折起使得平面 $A E D ⊥$ 平面 $D E B C$ ，连接 $A B ， A C$ ， $M ， N$ 分别是 $A D ， A C$ 的中点，如图2.

(1)、证明：在图2中 $E ， M ， N ， B$ 四点共面，且平面 $A D C ⊥$ 平面 $A E D$ ；

(2)、在图2中，若 $G$ 是线段 $A E$ 上一个动点，当直线 $C G$ 与平面 $B D G$ 所成角的正弦值取得最大值时，求 $G E$ 的长.

查看试题解析
19. 在某次现场招聘会上，某公司计划从甲和乙两位应聘人员中录用一位，规定从6个问题中随机抽取3个问题作答.假设甲能答对的题目有4道，乙每道题目能答对的概率为 $\frac{2}{3}$ ，

(1)、求甲在第一次答错的情况下，第二次和第三次均答对的概率；

(2)、请从期望和方差的角度分析，甲､乙谁被录用的可能性更大？

查看试题解析
20. $f (x) = x - a l n (1 + x)$ ，

(1)、讨论 $f (x)$ 的单调性；

(2)、当 $a = 1$ 时，证明 $f (x) \geq 0$ ；

(3)、证明对于任意正整数 $n$ ，都有 $\frac{1}{n} + \frac{1}{n + 1} + \frac{1}{n + 2} + ⋯ + \frac{1}{4 n - 1} + \frac{1}{4 n} > 2 l n 2$ .

查看试题解析
21. 已知椭圆 $E ： \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左焦点为 $F_{1} (- \sqrt{3} ， 0)$ ，点 $P (\sqrt{3} ， \frac{1}{2})$ 在 $E$ 上．

(1)、求椭圆 $E$ 的标准方程；

(2)、已知椭圆 $E$ 的上顶点为 $A$ ，圆 $M ： (x - 1)^{2} + y^{2} = r^{2} (r > 0)$ ，椭圆 $E$ 上是否存在两点 $B ， C$ 使得圆 $M$ 内切于 $△ A B C$ ？若存在，求出直线 $B C$ 的方程；若不存在，请说明理由．

查看试题解析
22. 在直角坐标系 $x O y$ 中，以坐标原点 $O$ 为极点， $x$ 轴正半轴为极轴建立极坐标系，半圆 $C$ 的极坐标方程为 $ρ + 4 s i n θ = 0 ， θ \in [π ， \frac{3 π}{2}]$ ．

(1)、求 $C$ 的参数方程；

(2)、已知点 $D$ 在 $C$ 上，若 $C$ 在 $D$ 处的切线与直线 $l ： y = \sqrt{3} x - 3$ 平行，求点 $D$ 的极坐标．

查看试题解析
23. 已知函数 $f (x) = 2 | x - 1 | - | x + 1 |$ ， $g (x) = | x - 1 |$ ．

(1)、在给出的坐标系中画出函数 $y = f (x)$ 的图像；

(2)、若关于 $x$ 的不等式 $f (x) \leq a g (x)$ 恒成立，求实数 $a$ 的取值范围．

查看试题解析