广西桂林市、崇左市2023届高三理数一模试卷

试卷更新日期：2023-04-13 类型：高考模拟

进入出卷网下载

一、单选题

1. 设集合 $A = {- 2 ， - 1 ， 0 ， 1 ， 2} ， B = {x ∣ 0 \leq x < \frac{5}{2}}$ ，则 $A ∩ B =$ （）

A、 ${0 ， 1 ， 2}$ B、 ${- 2 ， - 1 ， 0}$ C、 ${0 ， 1}$ D、 ${1 ， 2}$

查看试题解析
2. 在复平面内，复数 $i (2 - i)$ 对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 一个长方体去掉一个小长方体，所得几何体的正视图与侧（左）视图分别如图所示，则该几何体的俯视图为（）

A、 B、 C、 D、

查看试题解析
4. 某学校组建了演讲，舞蹈､航模､合唱，机器人五个社团，全校 $3000$ 名学生每人都参加且只参加其中一个社团，校团委从这 $3000$ 名学生中随机选取部分学生进行调查，并将调查结果绘制了如下不完整的两个统计图：

则选取的学生中参加机器人社团的学生数为（）

A、50 B、75 C、100 D、125

查看试题解析
5. 甲、乙两人各进行1次射击，如果两人击中目标的概率分别为0.8和0.4，则其中恰有1人击中目标的概率是(　　)

A、0.32 B、0.56 C、0.44 D、0.68

查看试题解析
6. 已知函数 $h (x)$ 是奇函数，且 $f (x) = h (x) + 2$ ，若 $x = 2$ 是函数 $y = f (x)$ 的一个零点，则 $f (- 2) =$ （）

A、-4 B、0 C、2 D、4

查看试题解析
7. 已知 $a = \frac{3}{2}$ ， $b = \frac{\sqrt{3}}{\sqrt{2}}$ ， $c = \frac{\ln 3}{\ln 2}$ ，则（）

A、 $a > b > c$ B、 $c > b > a$ C、 $c > a > b$ D、 $a > c > b$

查看试题解析
8. 已知圆 $C$ ： $x^{2} + y^{2} = 4$ ，直线 $L$ ： $y = k x + m$ ，则当 $k$ 的值发生变化时，直线被圆 $C$ 所截的弦长的最小值为 $2$ ，则 $m$ 的取值为（）

A、 $\pm 2$ B、 $\pm \sqrt{2}$ C、 $\pm \sqrt{3}$ D、 $\pm 3$

查看试题解析
9. 中国的古建筑往往是美学和哲学的完美体现.下图是某古建筑物及其剖面图， $A A^{^{'}} ， B B^{^{'}} ， C C^{^{'}} ， D D^{^{'}}$ 是桁， $D D_{1} ， C C_{1} ， B B_{1} ， A A_{1}$ 是脊， $O D_{1} ， D C_{1} ， C B_{1} ， B A_{1}$ 是相等的步，相邻桁的脊步的比分别为 $\frac{D D_{1}}{O D_{1}} = 0.5$ ， $\frac{C C_{1}}{D C_{1}} = k_{1}$ ， $\frac{B B_{1}}{C B_{1}} = k_{2}$ ， $\frac{A A_{1}}{B A_{1}} = k_{3}$ ，若 $k_{1} ， k_{2} ， k_{3}$ 是公差为0.15的等差数列， $t a n ∠ A O D_{1} = 0.65$ ，则 $k_{3} =$ （）

A、0.75 B、0.8 C、0.85 D、0.9

查看试题解析
10. 我国东汉末数学家赵爽在《周髀算经》中利用一副“弦图”给出了勾股定理的证明，后人称其为“赵爽弦图”，它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形，如图所示.在“赵爽弦图”中，若 $\vec{B C} = \vec{a} ， \vec{B A} = \vec{b} ， \vec{B E} = 3 \vec{E F}$ ，则 $\vec{A E} =$ （）

A、 $\frac{12}{25} \vec{a} - \frac{16}{25} \vec{b}$ B、 $\frac{16}{25} \vec{a} + \frac{12}{25} \vec{b}$ C、 $\frac{12}{25} \vec{a} + \frac{9}{25} \vec{b}$ D、 $\frac{9}{25} \vec{a} - \frac{12}{25} \vec{b}$

查看试题解析
11. 已知 $△ S A B$ 是边长为2的等边三角形， $∠ A C B = 45 °$ ，当三棱锥 $S - A B C$ 体积取最大时，其外接球的体积为（）

A、 $\frac{20 \sqrt{15} π}{27}$ B、 $\frac{28 π}{3}$ C、 $\frac{28 \sqrt{21} π}{27}$ D、 $\frac{20 π}{3}$

查看试题解析
12. 定义平面凸四边形为平面上每个内角度数都小于 $180 °$ 的四边形.已知在平面凸四边形 $A B C D$ 中， $∠ A = 30 ° ， ∠ B = 105 ° ， A B = \sqrt{3} ， A D = 2$ ，则 $C D$ 的取值范围是（）

A、 $[\frac{\sqrt{6} - \sqrt{2}}{4} ， 1)$ B、 $[\frac{\sqrt{6} - \sqrt{2}}{4} ， \frac{\sqrt{3} - 1}{2})$ C、 $[\frac{\sqrt{2}}{2} ， \frac{\sqrt{3} + 1}{2})$ D、 $[\frac{\sqrt{2}}{2} ， \sqrt{3} + 1)$

查看试题解析

二、填空题

13. 在 $(x^{3} - \frac{1}{x})^{4}$ 的展开式中，常数项为．

查看试题解析
14. 若 $\sin (\frac{π}{6} - α) = \frac{1}{3}$ ，则 $\cos^{2} (\frac{π}{6} + \frac{α}{2}) =$ .

查看试题解析
15. 写出一个值域为 $(- \infty ， 1)$ ，在区间 $(- \infty ， + \infty)$ 上单调递增的函数 $f (x) =$ ．

查看试题解析
16. 如图，一个光学装置由有公共焦点 $F_{1} ， F_{2}$ 的椭圆C与双曲线 $C^{'}$ 构成，一光线从左焦点 $F_{1}$ 发出，依次经过 $C^{'}$ 与C的反射，又回到点 $F_{1}$ .，历时m秒；若将装置中的 $C^{'}$ 去掉，则该光线从点 $F_{1}$ 发出，经过C两次反射后又回到点 $F_{1}$ 历时n秒，若 $C^{'}$ 的离心率为C的离心率的4倍，则 $\frac{m}{n} =$ .

查看试题解析

三、解答题

17. 从①前 $n$ 项和 $S_{n} = n^{2} + p (p \in R)$ ， ② $a_{n} = a_{n + 1} - 3$ ， ③ $a_{6} = 11$ 且 $2 a_{n + 1} = a_{n} + a_{n + 2}$ ，这三个条件中任选一个，补充到下面的问题中，并完成解答．
在数列 ${a_{n}}$ 中， $a_{1} = 1$ ， ____，其中 $n \in N^{*}$ ．

(1)、求 ${a_{n}}$ 的通项公式；

(2)、若 $a_{1} ， a_{n} ， a_{m}$ 成等比数列，其中 $m ， n \in N^{*}$ ，且 $m > n > 1$ ，求 $m$ 的最小值．

查看试题解析
18. 如图所示，在四棱锥 $P - A B C D$ 中， $A D / / B C$ ， $∠ B A D = 90 °$ ， $A B = A D = \frac{1}{2} B C = \sqrt{2}$ ， $P A = P B = P D = 2$ .

(1)、证明： $P A ⊥ B D$ ；

(2)、求直线BC与平面PCD所成角的余弦值.

查看试题解析
19. 某互联网公司为了确定下一季度的前期广告投入计划，收集了近 $6$ 个月广告投入量 $x$ （单位：万元）和收益（单位：万元）的数据如下表：
月份
$1$
$2$
$3$
$4$
$5$
$6$
广告投入量
$2$
$4$
$6$
$8$
$10$
$12$
收益
$14.21$
$20.31$
$31.8$
$31.18$
$37.83$
$44.67$
他们分别用两种模型① $y = b x + a$ ， ② $y = a e^{b x}$ 分别进行拟合，得到相应的回归方程并进行残差分析，得到如下图所示的残差图及一些统计量的值．
$\bar{x}$
$\bar{y}$
$\sum_{i = 1}^{6} x_{i} y_{i}$
$\sum_{i = 1}^{6} x_{i}^{2}$
$7$
$30$
$1464.24$
$364$
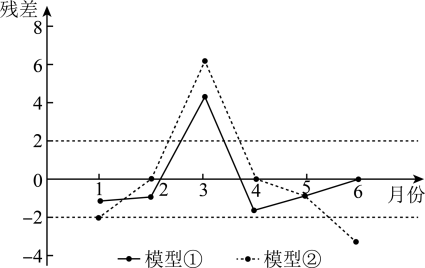
附：回归方程 $\hat{y} = \hat{b} x + \hat{a}$ 中斜率和截距的最小二乘估计公式分别为： $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \cdot \bar{y}}{\sum_{i - 1}^{n} {x_{i}}^{2} - n {\bar{x}}^{2}} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ．

(1)、根据残差图，比较模型①②的拟合效果，应该选择哪个模型？请说明理由．

(2)、残差绝对值大于 $2$ 的数据认为是异常数据，需要剔除．
（i）剔除异常数据后求出（1）中所选模型的回归方程；
（ii）若广告投入量 $x = 18$ ，求该模型收益的预报值是多少？

查看试题解析
20. 如图：小明同学先把一根直尺固定在画板上面，把一块三角板的一条直角边紧靠在直尺边沿，再取一根细绳，它的长度与另一直角边相等，让细绳的一端固定在三角板的顶点A处，另一端固定在画板上点F处，用铅笔尖扣紧绳子（使两段细绳绷直），靠住三角板，然后将三角板沿着直尺上下滑动，这时笔尖在平面上画出了圆锥曲线C的一部分图象.已知细绳长度为3，经测量，当笔尖运动到点P处，此时， $∠ F A P = 30 ° ， ∠ A F P = 90 °$ .设直尺边沿所在直线为a，以过F垂直于直尺的直线为x轴，以过F垂直于a的垂线段的中垂线为y轴，建立平面直角坐标系.

(1)、求曲线C的方程；

(2)、斜率为k的直线过点 $D (0 ， - 3)$ ，且与曲线C交于不同的两点M，N，已知k的取值范围为 $(0 ， 2)$ ，探究：是否存在 $λ$ ，使得 $\vec{D M} = λ \vec{D N}$ ，若存在，求出 $λ$ 的范围，若不存在，说明理由.

查看试题解析
21. 已知函数 $f (x) = e^{x} - a x + s i n x - 1$ ．

(1)、若函数 $f (x)$ 在 $(0 ， + ∞)$ 上单调递增，求实数 $a$ 的取值范围；

(2)、当 $1 \leq a < 2$ 时，求函数 $g (x) = (x - 2) f (x)$ 零点的个数．

查看试题解析
22. 在平面直角坐标 $x O y$ 中，曲线C的参数方程为 ${\begin{array}{l} x = \frac{2 \sqrt{t}}{1 + t} \\ y = \frac{2}{1 + t} \end{array}$ （ $t$ 为参数），以原点O为极点，x轴的正半轴为极轴建立极坐标系，直线 $l$ 的极坐标方程为 $\sqrt{2} ρ c o s (θ + \frac{π}{4}) + m = 0$ ．

(1)、写出曲线 $C$ 的普通方程；

(2)、若 $l$ 与 $C$ 有公共点，求 $m$ 的取值范围．

查看试题解析
23. 已知函数 $f (x) = | x + a | + 2 | x - 1 |$ ．

(1)、当 $a = 1$ 时，求 $f (x)$ 的最小值；

(2)、若 $a > 0$ ， $b > 0$ 时，对任意 $x \in [1 ， 2]$ 使得不等式 $f (x) > x^{2} - b + 1$ 恒成立，证明： ${(a + \frac{1}{2})}^{2} + {(b + \frac{1}{2})}^{2} > 2$ ．

查看试题解析

月份	$1$	$2$	$3$	$4$	$5$	$6$
广告投入量	$2$	$4$	$6$	$8$	$10$	$12$
收益	$14.21$	$20.31$	$31.8$	$31.18$	$37.83$	$44.67$

$\bar{x}$	$\bar{y}$	$\sum_{i = 1}^{6} x_{i} y_{i}$	$\sum_{i = 1}^{6} x_{i}^{2}$
$7$	$30$	$1464.24$	$364$