广西2023届高三理数模拟考试试卷
试卷更新日期:2023-04-13 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 若复数z的虚部小于0,且 , 则( )A、 B、 C、 D、3. 若函数的最大值为4,则函数的最小正周期为( )A、 B、 C、 D、4. 若双曲线C:的焦距大于6,C上一点到两焦点的距离之差的绝对值为d,则d的取值范围是( )A、 B、 C、 D、5. 某舞台灯光设备有一种25头LED矩阵灯(如图所示),其中有2头LED灯出现故障,假设每头LED灯出现故障都是等可能的,则这2头故障LED灯相邻(横向相邻或纵向相邻)的概率为( )
 A、 B、 C、 D、6. 若 , , 分别是定义在R上的偶函数、奇函数、偶函数,则下列函数不是偶函数的是( )A、 B、 C、 D、7. 如图,△ABC与△BCD都是正三角形, , 将△ABC沿BC边折起,使得A到达的位置,连接 , 得到三棱锥 , 则“”是“二面角为钝角”的( )
A、 B、 C、 D、6. 若 , , 分别是定义在R上的偶函数、奇函数、偶函数,则下列函数不是偶函数的是( )A、 B、 C、 D、7. 如图,△ABC与△BCD都是正三角形, , 将△ABC沿BC边折起,使得A到达的位置,连接 , 得到三棱锥 , 则“”是“二面角为钝角”的( ) A、充分不必要条件 B、充要条件 C、必要不充分条件 D、既不充分也不必要条件8. 已知A,B,C是同一条直线上三个不同的点,O为直线外一点.在正项等比数列中,已知 , , 则的公比q的取值范围是( )A、 B、 C、 D、9. 若x,y满足约束条件 , 则的取值范围是( )A、 B、 C、 D、10. 设钝角满足 , 则( )A、 B、 C、7 D、-711. 在四棱锥P-ABCD中,底面ABCD为梯形,平面PAD⊥底面ABCD, , , , , 则四棱锥P-ABCD外接球的表面积为( )A、26π B、27π C、28π D、29π12. 若函数的最小值为m,则函数的最小值为( )A、 B、 C、 D、
A、充分不必要条件 B、充要条件 C、必要不充分条件 D、既不充分也不必要条件8. 已知A,B,C是同一条直线上三个不同的点,O为直线外一点.在正项等比数列中,已知 , , 则的公比q的取值范围是( )A、 B、 C、 D、9. 若x,y满足约束条件 , 则的取值范围是( )A、 B、 C、 D、10. 设钝角满足 , 则( )A、 B、 C、7 D、-711. 在四棱锥P-ABCD中,底面ABCD为梯形,平面PAD⊥底面ABCD, , , , , 则四棱锥P-ABCD外接球的表面积为( )A、26π B、27π C、28π D、29π12. 若函数的最小值为m,则函数的最小值为( )A、 B、 C、 D、二、填空题
-
13. 若随机变量X的分布列为则X的数学期望为 .
X
-1
2
4
5
P
0.2
0.35
0.25
0.2
14. 南宋晚期的龙泉窑粉青釉刻花斗笠盏如图1所示,忽略杯盏的厚度,这只杯盏的轴截面如图2所示,其中光滑的曲线是抛物线的一部分,已知杯盏盛满茶水时茶水的深度为3cm,则该抛物线的焦点到准线的距离为cm. 15. 若不等式对恒成立,则a的取值范围是 .16. 有穷数列共有k项,满足 , , 且当 , 时, , 则项数k的最大值为 .
15. 若不等式对恒成立,则a的取值范围是 .16. 有穷数列共有k项,满足 , , 且当 , 时, , 则项数k的最大值为 .三、解答题
-
17. 在△ABC中,角A,B,C的对边分别为a,b,c.已知 .(1)、证明: .(2)、若D为BC的中点,从① , ② , ③这三个条件中选取两个作为条件证明另外一个成立.
注:若选择不同的组合分别解答,则按第一个解答计分.
18. 2016~2020年广西城乡居民人均可支配收入的柱形图如下图所示.
参考数据: , , .
附:样本的相关系数 ,
线性回归方程中的系数 , .
(1)、不考虑价格因素,求广西2020年农村居民人均可支配收入的年增长率(结果精确到0.1%).(2)、现欲了解广西各年城镇居民人均可支配收入y(单位:元)与农村居民人均可支配收入x(单位:元)是否存在较好的线性关系.设广西2016年城镇居民人均可支配收入为元,农村居民人均可支配收入为元,2017年对应的数据分别为 , , 2018年对应的数据分别为 , , 2019年对应的数据分别为 , , 2020年对应的数据分别为 , . 根据图中的五组数据,得到y关于x的线性回归方程为 . 试问y关于x的线性相关系数r是否大于0.95,并判断y与x之间是否存在较好的线性关系.19. 如图,四棱锥的底面为矩形, , , , 平面平面 . 是的中点,是上一点,且平面 .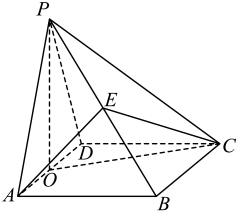 (1)、求的值;(2)、求直线与平面所成角的正弦值.20. 已知函数 .(1)、设 .
(1)、求的值;(2)、求直线与平面所成角的正弦值.20. 已知函数 .(1)、设 .①求曲线在点处的切线方程.
②试问有极大值还是极小值?并求出该极值.
(2)、若在上恰有两个零点,求a的取值范围.21. 已知椭圆 , 斜率为2的直线l与椭圆交于A,B两点.过点B作AB的垂线交椭圆于另一点C,再过点C作斜率为-2的直线交椭圆于另一点D.(1)、若坐标原点O到直线l的距离为 , 求△AOB的面积.(2)、试问直线AD的斜率是否为定值?若是定值,求出此定值;若不是定值,说明理由.