安徽省蚌埠市2023届高三理数第三次教学质量检查考试试卷
试卷更新日期:2023-04-13 类型:高考模拟
一、单选题
-
1. 设集合 , , 则( )A、 B、 C、 D、2. 已知为虚数单位,复数满足 , 则( )A、-1 B、1 C、 D、3. 已知 , 则( )A、 B、 C、-2 D、24. 直线与圆的位置关系是( )A、相交 B、相切 C、相离 D、无法确定5. 已知某地区中小学生人数如图①所示,为了解该地区中小学生的近视情况,卫生部门根据当地中小学生人数,用分层抽样的方法抽取了10%的学生进行调查,调查数据如图②所示,则估计该地区中小学生的平均近视率为( )
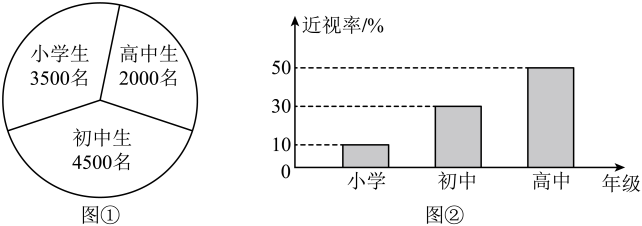 A、50% B、32% C、30% D、27%6. 若椭圆的离心率为 , 则椭圆的长轴长为( )A、6 B、或 C、 D、或7. 函数的图象大致为( )A、
A、50% B、32% C、30% D、27%6. 若椭圆的离心率为 , 则椭圆的长轴长为( )A、6 B、或 C、 D、或7. 函数的图象大致为( )A、 B、
B、 C、
C、 D、
D、 8. 在中,为上一点,且 , , , 则( )A、 B、 C、 D、
8. 在中,为上一点,且 , , , 则( )A、 B、 C、 D、二、多选题
-
9. 已知等差数列的前项和为 , 等比数列的前项积为 , 则下列结论正确的是( )A、数列是等差数列 B、数列是等差数列 C、数列是等比数列 D、数列是等差数列10. 已知是抛物线的焦点, , 是抛物线上相异两点,则以下结论正确的是( )A、若 , 那么 B、若 , 则线段的中点到轴的距离为 C、若是以为直角顶点的等腰三角形,则 D、若 , 则直线的斜率为11. 已知为圆锥底面圆的直径,点是圆上异于 , 的一点,为的中点, , 圆锥的侧面积为 , 则下列说法正确的是( )A、圆上存在点使平面 B、圆上存在点使平面 C、圆锥的外接球表面积为 D、棱长为的正四面体在圆锥内可以任意转动12. 已知 , 则下列结论正确的是( )A、 B、 C、 D、
三、填空题
-
13. 已知 , , , 则.14. 已知 , 则.15. 已知实数 , 且 , 则的最小值为.16. 已知定义在上的奇函数满足 , 且当时, , 则当时,;若对都有 , 则实数的取值范围为.
四、解答题
-
17. 某校为了丰富学生课余生活,组建了足球社团.为了解学生喜欢足球是否与性别有关,随机抽取了男、女同学各100名进行调查,部分数据如表所示:
喜欢足球
不喜欢足球
合计
男生
40
女生
30
合计
附:
0.1
0.05
0.01
0.005
0.001
2.706
3.841
6.635
7.879
10.828
(1)、根据所给数据完成上表,依据的独立性检验,能否认为该校学生喜欢足球与性别有关?(2)、社团指导老师从喜欢足球的学生中抽取了2名男生和1名女生示范点球射门.已知这两名男生进球的概率均为 , 这名女生进球的概率为 , 每人射门一次,假设各人射门相互独立,求3人进球总次数的分布列和数学期望.18. 已知函数.(1)、若 , 求函数的最小正周期;(2)、若图象在内有且仅有一条对称轴,求的取值范围.19. 已知数列满足 , , .(1)、求数列的通项公式;(2)、设 , 求证:.20. 如图,在四面体中,为的重心, , 分别在棱 , 上,平面平面. (1)、求的值;(2)、若平面 , , 且 , 求平面与平面的夹角的大小.
(1)、求的值;(2)、若平面 , , 且 , 求平面与平面的夹角的大小.