安徽省安庆市2023届高三数学模拟考试(二模)试卷
试卷更新日期:2023-04-13 类型:高考模拟
一、单选题
-
1. 已知集合 , , 则( )A、 B、 C、 D、2. 若复数满足(i是虚数单位),的共轭复数是 , 则的模是( )A、 B、4044 C、2 D、03. 为了解学生每天的体育活动时间,某市教育部门对全市高中学生进行调查,随机抽取1000名学生每天进行体育运动的时间,按照时长(单位:分钟)分成6组:第一组 , 第二组 , 第三组 , 第四组 , 第五组 , 第六组.对统计数据整理得到如图所示的频率分布直方图,则可以估计该市高中学生每天体育活动时间的第25百分位数约为( )
 A、43.5分钟 B、45.5分钟 C、47.5分钟 D、49.5分钟4. 已知非零向量 , 的夹角为 , , 且 , 则夹角的最小值为( )A、 B、 C、 D、5. 已知第二象限角满足 , 则的值为( )A、 B、 C、 D、6. 已知等差数列满足 , 则不可能取的值是( )A、-3 B、 C、 D、7. 已知函数 , 若函数恰有3个零点,则实数的取值范围是( )A、 B、 C、 D、8. 一底面半径为1的圆柱,被一个与底面成45°角的平面所截(如图),为底面圆的中心,为截面的中心,为截面上距离底面最小的点,到圆柱底面的距离为1,为截面图形弧上的一点,且 , 则点到底面的距离是( )
A、43.5分钟 B、45.5分钟 C、47.5分钟 D、49.5分钟4. 已知非零向量 , 的夹角为 , , 且 , 则夹角的最小值为( )A、 B、 C、 D、5. 已知第二象限角满足 , 则的值为( )A、 B、 C、 D、6. 已知等差数列满足 , 则不可能取的值是( )A、-3 B、 C、 D、7. 已知函数 , 若函数恰有3个零点,则实数的取值范围是( )A、 B、 C、 D、8. 一底面半径为1的圆柱,被一个与底面成45°角的平面所截(如图),为底面圆的中心,为截面的中心,为截面上距离底面最小的点,到圆柱底面的距离为1,为截面图形弧上的一点,且 , 则点到底面的距离是( )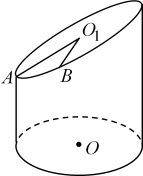 A、 B、 C、 D、
A、 B、 C、 D、二、多选题
-
9. 将函数图象上点的横坐标缩短为原来的倍,然后将所得图象向右平移个单位,得到函数的图象.则下列说法中正确的是( )A、函数的最小正周期为 B、函数的图象有一条对称轴为 C、函数的单调递增区间为 D、函数在区间上的值域为10. 在三棱锥中, , , , 分别是 , , , 的重心.则下列命题中正确的有( )A、平面 B、 C、四条直线 , , , 相交于一点 D、11. 牛顿用“作切线”的方法求函数的零点时,给出了“牛顿数列”,它在航空航天中应用非常广泛,其定义是:对于函数和数列 , 若 , 则称数列为牛顿数列.已知函数 , 数列为牛顿数列,且 , , , 则下列结论中正确的是( )A、 B、 C、是等比数列 D、12. 已知、为抛物线上两点,以 , 为切点的抛物线的两条切线交于点 , 设以 , 为切点的抛物线的切线斜率为 , , 过 , 的直线斜率为 , 则以下结论正确的有( )A、 , , 成等差数列; B、若点的横坐标为 , 则; C、若点在抛物线的准线上,则不是直角三角形; D、若点在直线上,则直线恒过定点;
三、填空题
-
13. 设某批产品中,甲、乙、丙三个车间生产的产品分别占45%、35%、20%,甲、乙车间生产的产品的次品率分别为2%和3%.现从中任取一件,若取到的是次品的概率为2.95%,则推测丙车间的次品率为.14. 在棱长为4的正方体中,点是棱上一点,且.过三点、、的平面截该正方体的内切球,所得截面圆面积的大小为.15. 已知双曲线 , 的两个焦点分别为 , , 过轴上方的焦点的直线与双曲线上支交于 , 两点,以为直径的圆经过点 , 若 , , 成等差数列,则该双曲线的渐近线方程为.16. 已知函数 , 其中 , 若不等式对任意恒成立,则的最小值为.
四、解答题
-
17. 已知公差不为0的等差数列的前项和为 , , 且 , , 成等比数列.(1)、求数列的通项公式;(2)、设 , 求数列的前项和.18. 在中,角 , , 所对的边分别为 , , , .(1)、若角 , 求角的大小;(2)、若 , , 求.19. 如图,在四棱锥中,底面是梯形, , , , 侧面是等边三角形,侧面是等腰直角三角形,.
 (1)、求证:平面;(2)、若是棱上的一点,且平面.求平面与平面所成二面角的余弦值.20. 为了“锤炼党性修养,筑牢党性根基”,党员教师小A每天自觉登录“学习强国APP”,参加各种学习活动,同时热衷于参与四人赛.每局四人赛是由网络随机匹配四人进行比赛,每题回答正确得20分,第1个达到100分的比赛者获得第1名,赢得该局比赛,该局比赛结束.每天的四人赛共有30局,前2局是有效局,根据得分情况获得相应名次,从而得到相应的学习积分,第1局获得第1名的得3分,获得第2、3名的得2分,获得第4名的得1分;第2局获得第1名的得2分,获得第2、3、4名的得1分;后28局是无效局,无论获得什么名次,均不能获得学习积分.经统计,小A每天在第1局四人赛中获得3分、2分、1分的概率分别为 , , , 在第2局四人赛中获得2分、1分的概率分别为 , .(1)、设小A每天获得的得分为 , 求的分布列、数学期望和方差;(2)、若小A每天赛完30局,设小A在每局四人赛中获得第1名从而赢得该局比赛的概率为 , 每局是否赢得比赛相互独立,请问在每天的30局四人赛中,小A赢得多少局的比赛概率最大?
(1)、求证:平面;(2)、若是棱上的一点,且平面.求平面与平面所成二面角的余弦值.20. 为了“锤炼党性修养,筑牢党性根基”,党员教师小A每天自觉登录“学习强国APP”,参加各种学习活动,同时热衷于参与四人赛.每局四人赛是由网络随机匹配四人进行比赛,每题回答正确得20分,第1个达到100分的比赛者获得第1名,赢得该局比赛,该局比赛结束.每天的四人赛共有30局,前2局是有效局,根据得分情况获得相应名次,从而得到相应的学习积分,第1局获得第1名的得3分,获得第2、3名的得2分,获得第4名的得1分;第2局获得第1名的得2分,获得第2、3、4名的得1分;后28局是无效局,无论获得什么名次,均不能获得学习积分.经统计,小A每天在第1局四人赛中获得3分、2分、1分的概率分别为 , , , 在第2局四人赛中获得2分、1分的概率分别为 , .(1)、设小A每天获得的得分为 , 求的分布列、数学期望和方差;(2)、若小A每天赛完30局,设小A在每局四人赛中获得第1名从而赢得该局比赛的概率为 , 每局是否赢得比赛相互独立,请问在每天的30局四人赛中,小A赢得多少局的比赛概率最大?
