2023年高三数学解三角形二轮专题复习
试卷更新日期:2023-04-13 类型:二轮复习
一、单选题
-
1. 已知 , 且函数恰有两个极大值点在 , 则的取值范围是( )A、 B、 C、 D、2. 在中,角A,B,C对边分别为a,b,c.命题 , 命题为等腰三角形.则p是q的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件3. 已知函数的部分图象如图所示,( )
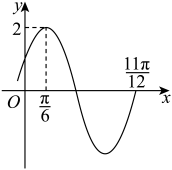 A、 B、-1 C、 D、
A、 B、-1 C、 D、二、多选题
-
4. 在中,角 , ,的对边分别为 , , , 若 , 且 , 则不可能为( )A、等腰直角三角形 B、等边三角形 C、锐角三角形 D、钝角三角形5. 在平面直角坐标系中,已知点 , 则( )A、 B、是直角三角形 C、在方向上的投影向量的坐标为 D、与垂直的单位向量的坐标为或6. 在中,内角、、所对的边分别为、、 , 的面积为 , 下列与有关的结论,正确的是( )A、若为锐角三角形,则 B、若 , 则 C、若 , 则一定是等腰三角形 D、若为非直角三角形,则7. 已知 , , 是单位圆上的三点,满足 , , 且 , 其中为非零常数,则下列结论一定正确的有( )A、若 , 则 B、若 , 则 C、 D、
三、填空题
-
8. 在平面直角坐标系中,若角的顶点为坐标原点,始边与x轴的非负半轴重合,终边与以点O为圆心的单位圆交于点 , 则的值为.9. 已知函数 , 则下列说法中正确的是 .
①一条对称轴为;
②将图象向右平移个单位,再向下平移1个单位得到的新函数为奇函数;
③若 , 则;
④若函数在区间上恰有2个极大值点,则实数的取值范围是 .
10. 神舟十三号三位航天英雄在太空出差180余天后,顺利返回地面.如图,返回舱达到一定高度时,近似垂直落地,在下落过程中的某时刻位于点 , 预计垂直落在地面点处,在地面同一水平线上的A、B两个观测点,分别观测到点的仰角为15°,45°,若千米,则点距离地面的高度约为千米(参考数据:).
四、解答题
-
11. 记的内角的对边分别为 , 满足 , 是边上的点,且.(1)、求;(2)、求的最小值.12. 近期,宁波市多家医院发热门诊日接诊量显著上升,为了应对即将到来的新冠病毒就诊高峰,某医院计划对原有的发热门诊进行改造,如图所示,原发热门诊是区域(阴影部分),以及可利用部分为区域 , 其中 , 米,米,区域为三角形,区域为以为半径的扇形,且.
 (1)、为保证发热门诊与普通诊室的隔离,需在区域外轮廓设置隔离带,求隔离带的总长度;(2)、在可利用区域中,设置一块矩形作为发热门诊的补充门诊,求补充门诊面积最大值.13. 在△ABC中,角A,B,C的对边长依次是a,b,c, , .(1)、求角B的大小;(2)、当△ABC面积最大时,求∠BAC的平分线AD的长.
(1)、为保证发热门诊与普通诊室的隔离,需在区域外轮廓设置隔离带,求隔离带的总长度;(2)、在可利用区域中,设置一块矩形作为发热门诊的补充门诊,求补充门诊面积最大值.13. 在△ABC中,角A,B,C的对边长依次是a,b,c, , .(1)、求角B的大小;(2)、当△ABC面积最大时,求∠BAC的平分线AD的长.