四川省绵阳市江油市八校联考2022-2023学年八年级下学期3月月考数学试题

试卷更新日期：2023-04-13 类型：月考试卷

进入出卷网下载

一、选择题（共12小题，每小题3分，共36分）

1. 若二次根式 $\sqrt{x - 5}$ 有意义，则x的取值范围是（）

A、x＞5 B、x≥-5 C、x＜5 D、x≥5

查看试题解析
2. 下列二次根式中属于最简二次根式的是（）

A、 $\sqrt{24}$ B、 $\sqrt{16}$ C、 $\sqrt{7}$ D、 $\sqrt{0.2}$

查看试题解析
3. 下列运算中，正确的是（）

A、 $\sqrt{24}$ ÷ $\sqrt{6}$ ＝2 B、 $\sqrt{25}$ ＝±5 C、5 $\sqrt{2}$ − $\sqrt{2}$ ＝5 D、 $\sqrt{5}$ − $\sqrt{3}$ ＝ $\sqrt{2}$

查看试题解析
4. 下列计算正确的是（）

A、 $5 \sqrt{5}$ - $4 \sqrt{5}$ =1 B、 $\sqrt{3}$ + $\sqrt{2}$ = $\sqrt{6}$ C、 $\sqrt{3}$ + $\sqrt{2}$ = $\sqrt{5}$ D、 $3 \sqrt{5}$ +2 $\sqrt{5}$ = $5 \sqrt{5}$

查看试题解析
5. 已知x＝ $\sqrt{3}$ +1，则x²-2x+1的值为（）

A、0 B、3 C、1 D、 $\sqrt{2} + 1$

查看试题解析
6. 已知实数a在数轴上的位置如图所示，则化简： $| a - 2 |$ + $\sqrt{{(a - 4)}^{2}}$ 的结果为（）

A、2 B、-2 C、2a-6 D、-2a+6

查看试题解析
7. 一个直角三角形，两直角边长分别为6和8，下列说法正确的是（）

A、斜边长为36 B、三角形的周长为64 C、斜边上的高为4.8 D、三角形面积为48

查看试题解析
8. 如图，在△ABC中，∠ACB＝90°，CD⊥AB，垂足为D．若AC＝3，BC＝4，则CD的长为（）

A、2.4 B、2.5 C、4.8 D、5

查看试题解析
9. 如图所示的是由两个直角三角形和三个正方形组成的图形，其中阴影部分的面积是（）

A、50 B、16 C、25 D、41

查看试题解析
10. △ABC的三条边分别为a，b，c，下列条件不能判断△ABC是直角三角形的是（）

A、b²＝（a+c）（a-c） B、∠A＝∠B+∠C C、∠A：∠B：∠C＝3：4：5 D、a＝6，b＝8，c＝10

查看试题解析
11. 下列四组数，是勾股数的是（）

A、0.3，0.4，0.5 B、3，4，5 C、6，7，8 D、3² ， 4² ， 5²

查看试题解析
12. 如图，某自动感应门的正上方A处装着一个感应器，离地面的高度AB为2.5米，一名学生站在C处时，感应门自动打开了，此时这名学生离感应门的距离BC为1.2米，头顶离感应器的距离AD为1.5米，则这名学生身高CD为（）米．

A、0.9 B、1.3 C、1.5 D、1.6

查看试题解析

二、填空题（每小题3分，共18分）

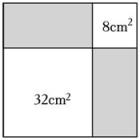
13. 最简二次根式 $\sqrt{4 - 3 x}$ 与二次根式 $\sqrt{8}$ 是同类二次根式，则x＝．

查看试题解析
14. 已知x＝2+ $\sqrt{5}$ ， y＝2- $\sqrt{5}$ ，则代数式x²+y²的值为．

查看试题解析
15. 如图，从一个大正方形中可以裁去面积为8cm²和32cm²的两个小正方形，则大正方形的边长为．

查看试题解析
16. 如图所示，已知△ABC中，BC＝16cm，AC＝20cm，AB＝12cm，点P是BC边上的一个动点，点P从点B开始沿B→C→A方向运动，且速度为每秒2cm，设运动的时间为t（s），若△ABP是以AB为腰的等腰三角形，则运动时间t＝．

查看试题解析
17. 某会展中心在会展期间准备将高5m、长13m、宽2m的楼道铺上地毯，已知地毯每平方米20元，请你帮助计算一下，铺完这个楼道至少需要元．

查看试题解析
18. 在《九章算术》中有一个问题（如图)：今有竹高一丈，末折抵地，去本三尺，问折者高几何?它的意思是：一根竹子原高一丈（ $10$ 尺)，中部一处折断，竹梢触地面处离竹根 $3$ 尺，试问折断处离地面尺．

查看试题解析

三、解答题（共6小题，共48分）

19. 已知 $a = 3 + 2 \sqrt{2}$ ， $b = 3 - 2 \sqrt{2}$ ，分别求下列代数式的值：

(1)、a²-b²；

(2)、a²-2ab+b² ．

查看试题解析
20. 计算： $\sqrt{18} - {(\sqrt{2} + 1)}^{2} + (\sqrt{3} + 1) (\sqrt{3} - 1)$ ．

查看试题解析
21. 如图，正方形ABCD的面积为8，正方形ECFG的面积为32.

(1)、求正方形ABCD和正方形ECFG的边长；

(2)、求阴影部分的面积.

查看试题解析
22. 如图，四边形ABCD中，AB＝20，BC＝15，CD＝7，AD＝24，∠B＝90°．

(1)、判断∠D是否是直角，并说明理由．

(2)、求四边形ABCD的面积．

查看试题解析
23. 如图，在笔直的公路AB旁有一座山，为方便运输货物现要从公路AB上的D处开凿隧道修通一条公路到C处，已知点C与公路上的停靠站A的距离为15km，与公路上另一停靠站B的距离为20km，停靠站A、B之间的距离为25km，且CD⊥AB．

(1)、求修建的公路CD的长；

(2)、若公路CD修通后，一辆货车从C处经过D点到B处的路程是多少？

查看试题解析
24. 如图，在Rt△ABC中，∠C＝90°，AB＝10cm，AC＝6cm，动点P从点B出发沿射线BC以2cm/s的速度移动，设运动的时间为t秒．

(1)、求BC边的长；

(2)、当△ABP为直角三角形时，求t的值；

(3)、当△ABP为等腰三角形时，求t的值．

查看试题解析