浙江省金华市永康三中教育集团2022-2023学年九年级下学期第一次独立作业数学试卷
试卷更新日期:2023-04-13 类型:月考试卷
一、选择题(本大题共10小题,共30.0分。)
-
1. -5的倒数是( )A、-5 B、5 C、 D、2. 肥皂泡的泡壁厚度大约是0.00000071米,数字0.00000071用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、2x+3y=5xy B、 C、 D、a10÷a5=a54. 抛一枚均匀的骰子,下列事件中,发生可能性最大的是( )A、点数是奇数 B、点数是3的倍数 C、点数大于5 D、点数小于55. 若⊙P的半径为13,圆心P的坐标为(5, 12 ),则平面直角坐标系的原点O与⊙P的位置关系是( )
A、在⊙P内 B、在⊙P上 C、在⊙P外 D、无法确定6. 如图是一只茶壶,从不同方向看这只茶壶,你认为是俯视效果图的是( ) A、
A、 B、
B、 C、
C、 D、
D、 7. 已知点与点关于轴对称,则代数式值为( )A、-6 B、6 C、4 D、-48. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )
7. 已知点与点关于轴对称,则代数式值为( )A、-6 B、6 C、4 D、-48. 如图,某校教学楼与的水平间距 , 在教学楼的顶部点测得教学楼的顶部点的仰角为 , 测得教学楼的底部点的俯角为 , 则教学楼的高度是( )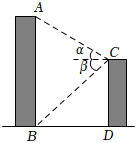 A、 B、 C、 D、9. 已知 , 关于的一元二次方程的解为 , , 则下列结论正确的是( )A、 B、 C、 D、10. 如图1是由四个全等的直角三角形组成的“风车”图案,其中 , 延长直角三角形的斜边恰好交于另一直角三角形的斜边中点,得到如图2,若 , 则该“风车”的面积为( )
A、 B、 C、 D、9. 已知 , 关于的一元二次方程的解为 , , 则下列结论正确的是( )A、 B、 C、 D、10. 如图1是由四个全等的直角三角形组成的“风车”图案,其中 , 延长直角三角形的斜边恰好交于另一直角三角形的斜边中点,得到如图2,若 , 则该“风车”的面积为( )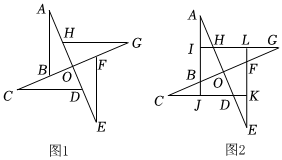 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本大题共6小题,共24.0分)
-
11. 若根式有意义,则实数的取值范围是.12. 已知 ,则 . .13. 已知一个圆锥的侧面积为 , 母线长为6,则它的底面半径为 .14. 如图,在中, , 边在轴上,顶点 , 的坐标分别为和将正方形沿轴向右平移,当点落在边上时,平移的距离为 .
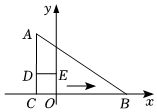 15. 如图,在平行四边形中, , 利用尺规在 , 上分别截取 , , 使;分别以、为圆心,大于的长为半径作弧,两弧在内交于点;作射线交于点若 , 则的长为 .
15. 如图,在平行四边形中, , 利用尺规在 , 上分别截取 , , 使;分别以、为圆心,大于的长为半径作弧,两弧在内交于点;作射线交于点若 , 则的长为 .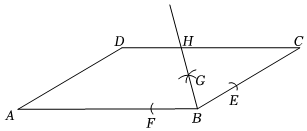 16. 随着“科学运动、健康生活”的理念深入人心,跑步机已成为家居新宠,某品牌跑步机如图1)的跑道可以旋转如图2),图为跑道绕点旋转到位置时的侧面图,其中为显示屏,为扶手,点 , , 在同一直线上,为可伸缩液压支撑杆,、的位置不变,的长度可变化.
16. 随着“科学运动、健康生活”的理念深入人心,跑步机已成为家居新宠,某品牌跑步机如图1)的跑道可以旋转如图2),图为跑道绕点旋转到位置时的侧面图,其中为显示屏,为扶手,点 , , 在同一直线上,为可伸缩液压支撑杆,、的位置不变,的长度可变化. (1)、已知 , , , 则 ;(2)、在(1)的条件下,若 , , , 且、、恰好在同一直线上,则 .
(1)、已知 , , , 则 ;(2)、在(1)的条件下,若 , , , 且、、恰好在同一直线上,则 .三、解答题(本大题共8小题,共62.0分。)
-
17. 计算:18. 化简:.19. 如图,有一段斜坡长为10米,坡角 , 为方便残疾人的轮椅车通行,现准备把坡角降为.
 (1)、求坡高;(2)、求斜坡新起点与原起点的距离精确到0.1米.
(1)、求坡高;(2)、求斜坡新起点与原起点的距离精确到0.1米.参考数据: , ,
20. 图①、图②、图③均是的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1,点A、B、C、D均在格点上在图②、图③中,只用无刻度的直尺,在给定的正方形网格中,按要求画图,保留作图痕迹,不要求写出画法.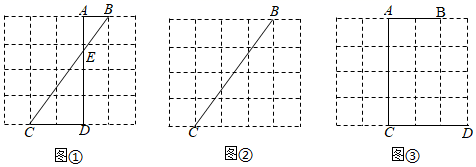 (1)、如图①, .(2)、如图②,在上找一点F,使 .(3)、如图③,在上找一点M,连结、 , 使 .21. 我区某中学举行了“垃圾分类,绿色环保”知识竞赛活动,根据学生的成绩划分为A,B,C,D四个等级,并绘制了不完整的两种统计图:
(1)、如图①, .(2)、如图②,在上找一点F,使 .(3)、如图③,在上找一点M,连结、 , 使 .21. 我区某中学举行了“垃圾分类,绿色环保”知识竞赛活动,根据学生的成绩划分为A,B,C,D四个等级,并绘制了不完整的两种统计图: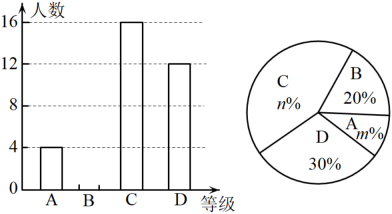
根据图中提供的信息,回答下列问题:
(1)、参加知识竞赛的学生共有 ▲ 人,并把条形统计图补充完整;(2)、扇形统计图中, , C等级对应的圆心角为度;(3)、小明是四名获A等级的学生中的一位,学校将从获A等级的学生中任选取2人,参加区举办的知识竞赛,请用列表法或画树状图,求小明被选中参加区知识竞赛的概率.22. 如图,已知内接于 , 平分交于点 , 过点作的平行线分别交、的延长线于点、 , 连接.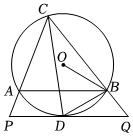 (1)、求证:是的切线;(2)、连接 , 若 , 圆的半径为10,求的长.23. 如图 , 地面上两根等长立柱 , 之间悬挂一根近似成抛物线的绳子.解答下列问题:
(1)、求证:是的切线;(2)、连接 , 若 , 圆的半径为10,求的长.23. 如图 , 地面上两根等长立柱 , 之间悬挂一根近似成抛物线的绳子.解答下列问题: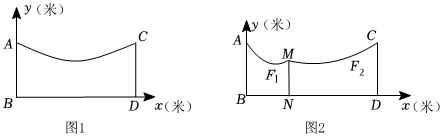 (1)、两根等长立柱 , 的高度是 ▲ 米;并求出绳子最低点离地面的距离.(2)、因实际需要,在离为3米的位置处用一根立柱撑起绳子如图2),使左边抛物线的最低点距为米,离地面2米,求的长.(3)、将立柱的长度提升为3米,通过调整的位置,使抛物线对应函数的二次项系数始终为 , 设离的距离为米,抛物线的顶点离地面距离为米,当时,求的取值范围.24. 如图,菱形中, , , 点是射线上的一个动点,将线段绕点顺时针旋转到 , 连接、.
(1)、两根等长立柱 , 的高度是 ▲ 米;并求出绳子最低点离地面的距离.(2)、因实际需要,在离为3米的位置处用一根立柱撑起绳子如图2),使左边抛物线的最低点距为米,离地面2米,求的长.(3)、将立柱的长度提升为3米,通过调整的位置,使抛物线对应函数的二次项系数始终为 , 设离的距离为米,抛物线的顶点离地面距离为米,当时,求的取值范围.24. 如图,菱形中, , , 点是射线上的一个动点,将线段绕点顺时针旋转到 , 连接、.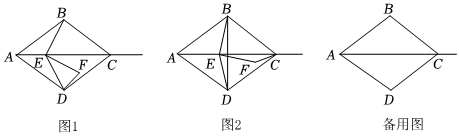 (1)、求证:;(2)、如图2,连接 , , 当与相似时,求的长;(3)、当点关于直线的对称点落在菱形的边上时,求的长.
(1)、求证:;(2)、如图2,连接 , , 当与相似时,求的长;(3)、当点关于直线的对称点落在菱形的边上时,求的长.