四川省南充市2023年中考数学一诊试卷
试卷更新日期:2023-04-13 类型:中考模拟
一、选择题(本大题共10小题,共40.0分。)
-
1. 的值是( )A、-1 B、1 C、5 D、-52. 我国古代数学家祖冲之推算出的近似值为 , 它与的误差小于0.0000003.将0.0000003用科学记数法可以表示为( )A、 B、 C、 D、3. 如图,在由4个相同的小正方形拼成的网格中,( )
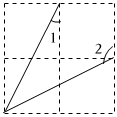 A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图, 与正五边形 的两边 相切于 两点,则 的度数是( )
A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图, 与正五边形 的两边 相切于 两点,则 的度数是( )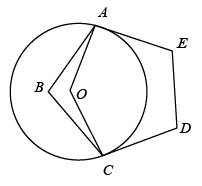 A、 B、 C、 D、6. 垃圾分类利国利民,某校宣传小组就“空矿泉水瓶应投放到哪种颜色的垃圾收集桶内”进行统计活动,他们随机采访50名学生并作好记录.以下是排乱的统计步骤:
A、 B、 C、 D、6. 垃圾分类利国利民,某校宣传小组就“空矿泉水瓶应投放到哪种颜色的垃圾收集桶内”进行统计活动,他们随机采访50名学生并作好记录.以下是排乱的统计步骤:①从扇形统计图中分析出本校学生对空矿泉水瓶投放的正确率;
②整理采访记录并绘制空矿泉水瓶投放频数分布表;
③绘制扇形统计图来表示空矿泉水瓶投放各收集桶所占的百分比.
正确统计步骤的顺序应该是( )A、②→③→① B、②→①→③ C、③→①→② D、③→②→①7. 数学兴趣小组利用无人机测量学校旗杆高度,已知无人机的飞行高度为37米,当无人机与旗杆的水平距离是45米时,观测旗杆顶部的俯角为 , 则旗杆的高度约为( ) A、米 B、 C、 D、22.5米8. 如图,在菱形中, , , 则的值是( )
A、米 B、 C、 D、22.5米8. 如图,在菱形中, , , 则的值是( ) A、 B、 C、 D、9. 如图,在平面直角坐标系中,直线与反比例函数的图象交于点 , 将直线沿轴向上平移个单位长度,交轴于点 , 交反比例函数图象于点 , 若 , 则的值为( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,直线与反比例函数的图象交于点 , 将直线沿轴向上平移个单位长度,交轴于点 , 交反比例函数图象于点 , 若 , 则的值为( ) A、1.5 B、2 C、2.5 D、310. 二次函数图象如图,下列结论:
A、1.5 B、2 C、2.5 D、310. 二次函数图象如图,下列结论:;;当时,;;若 , 且 , 则.
其中正确的有( )

A、①②③ B、①②④ C、③④⑤ D、②③⑤二、填空题(本大题共6小题,共24.0分)
-
11. 计算的结果是 .12. 在平面直角坐标系中,点与点关于轴对称,则点的坐标是 .13. 如图,是由四个直角边分别为3和4的全等的直角三角形拼成的“赵爽弦图”,小亮随机的往大正方形区域内投针一次,则针扎在阴影部分的概率是.
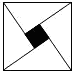 14. 若将半径为8,圆心角为的扇形围成一个圆锥体,则圆锥体底面圆的半径最大为 .15. 点在函数的图象上,则代数式的值等于 .16. 如图,在矩形中, , 分别是线段 , 上的两个动点,若 , , 则的最小值为 .
14. 若将半径为8,圆心角为的扇形围成一个圆锥体,则圆锥体底面圆的半径最大为 .15. 点在函数的图象上,则代数式的值等于 .16. 如图,在矩形中, , 分别是线段 , 上的两个动点,若 , , 则的最小值为 .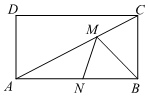
三、解答题(本大题共9小题,共86.0分。)
-
17. 计算:.18. 如图,点、、、在同一条直线上, , , .
求证:.
 19. 在学习“一次函数的图象和性质”时,李老师设计了一个数学活动有、两组卡片,每组各3张,每张卡片除正面写有不同数字外,其余均相同组卡片上分别写有0,2,3;组卡片上分别写有-5,-1,1甲从组中随机抽取一张记为 , 乙从组中随机抽取一张记为.(1)、若甲抽出的数字是2,乙抽出的数是-1,得到的坐标在函数的图象上,求的值;(2)、在(1)的条件下,求甲、乙随机抽取的数得到坐标恰在函数的图象上的概率请用树形图或列表法求解20. 关于的一元二次方程中,、、是的三条边,其中.(1)、求证此方程有两个不相等的实数根;(2)、若方程的两个根是、 , 且 , 求::.21. 如图,点在第一象限,轴,垂足为 , , , 反比例函数的图象经过的中点.
19. 在学习“一次函数的图象和性质”时,李老师设计了一个数学活动有、两组卡片,每组各3张,每张卡片除正面写有不同数字外,其余均相同组卡片上分别写有0,2,3;组卡片上分别写有-5,-1,1甲从组中随机抽取一张记为 , 乙从组中随机抽取一张记为.(1)、若甲抽出的数字是2,乙抽出的数是-1,得到的坐标在函数的图象上,求的值;(2)、在(1)的条件下,求甲、乙随机抽取的数得到坐标恰在函数的图象上的概率请用树形图或列表法求解20. 关于的一元二次方程中,、、是的三条边,其中.(1)、求证此方程有两个不相等的实数根;(2)、若方程的两个根是、 , 且 , 求::.21. 如图,点在第一象限,轴,垂足为 , , , 反比例函数的图象经过的中点.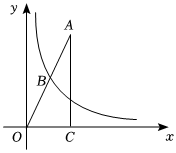 (1)、求值;(2)、若直线与反比例函数图象在第一象限有交点,求的取值范围.22. 如图,是的内接三角形,为的直径,过点的直线交的延长线于点 , 连接 , 且 , .
(1)、求值;(2)、若直线与反比例函数图象在第一象限有交点,求的取值范围.22. 如图,是的内接三角形,为的直径,过点的直线交的延长线于点 , 连接 , 且 , . (1)、求证:是的切线;(2)、若 , , , 求的值.23. 某批发市场批发甲、乙两种水果,甲种水果的销售利润万元与进货量吨近似满足函数关系;乙种水果的销售利润万元与进货量吨近似满足函数关系其中 , , 为常数 , 且进货量为吨时,销售利润为1.4万元;进货量为2吨时,销售利润为2.6万元.(1)、求万元与吨之间的函数关系式;(2)、如果市场准备进甲、乙两种水果共10吨,设乙种水果的进货量为吨,销售完毕,这两种水果所获最大利润是多少?
(1)、求证:是的切线;(2)、若 , , , 求的值.23. 某批发市场批发甲、乙两种水果,甲种水果的销售利润万元与进货量吨近似满足函数关系;乙种水果的销售利润万元与进货量吨近似满足函数关系其中 , , 为常数 , 且进货量为吨时,销售利润为1.4万元;进货量为2吨时,销售利润为2.6万元.(1)、求万元与吨之间的函数关系式;(2)、如果市场准备进甲、乙两种水果共10吨,设乙种水果的进货量为吨,销售完毕,这两种水果所获最大利润是多少?

