广西壮族自治区河池市凤山县2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-04-13 类型：期中考试

进入出卷网下载

一、单选题

1. 4的算术平方根是（）

A、-2 B、2 C、 $\pm 2$ D、 $\sqrt{2}$

查看试题解析
2. 平面直角坐标系中，点 $A (- 2 ， a)$ 位于x轴的上方，则a的值可以是（）

A、0 B、－1 C、 $\sqrt{3}$ D、±3

查看试题解析
3. 下列实数： $3 ， 0 ， - \sqrt{2} ， 0.35$ ，其中最小的实数是（）

A、3 B、0 C、 $- \sqrt{2}$ D、0.35

查看试题解析
4. 小宁同学在体育课上进行跳远测试，体育老师在测量他的跳远成绩时，用到数学基本原理，最恰当的是两点之间（）

A、线段最短 B、垂线段最短 C、在同一平面内，过一点有且只有一条直线与已知直线垂直 D、经过直线外一点，有且只有一条直线与这条直线平行

查看试题解析
5. 如图，小聪把一块含有 $60 °$ 角的直角三角形板的两个顶点放在直尺的对边上，并测得 $∠ 1 = 25 °$ ，则 $∠ 2$ 的度数是（）

A、 $35 °$ B、 $30 °$ C、 $25 °$ D、 $60 °$

查看试题解析
6. 如图，数轴上有A，B，C，D四点，根据各点的位置，所表示的数与 $5 - \sqrt{10}$ 最接近的点是（）

A、A B、B C、C D、D

查看试题解析
7. 下列命题中，假命题是（）

A、若A(a，b)在x轴上，则B(b，a)在y轴上 B、如果直线a，b，c满足a∥b，b∥c，那么a∥c C、两直线平行，同旁内角互补 D、相等的两个角是对顶角

查看试题解析
8. 如图是围棋棋盘的一部分，将它放置在某个平面直角坐标系中，若白棋②的坐标为（－3，－1），白棋④的坐标为（－2，－5），则黑棋①的坐标为（）

A、（－1，－4） B、（1，－4） C、（3，1） D、（－3，－1）

查看试题解析
9. 在平面直角坐标系中，已知x轴上的点P到y轴的距离为3，则点P的坐标为（）

A、（3，0） B、（0，3）或（0，-3） C、（0，3） D、（3，0）或（-3，0）

查看试题解析
10. 如图，下列命题：①若∠1＝∠2，则∠D＝∠4；②若∠C＝∠D，则∠4＝∠C；③若∠A＝∠F，则∠1＝∠2；④若∠1＝∠2，∠C＝∠D，则∠A＝∠F；⑤若∠C＝∠D，∠A＝∠F，则∠1＝∠2.其中正确的个数有（）个.

A、1 B、2 C、3 D、4

查看试题解析
11. 在平面直角坐标系中，将点P（﹣2，1）向右平移3个单位长度，再向上平移4个单位长度得到点P′的坐标是（）

A、（2，4） B、（1，5） C、（1，-3） D、（-5，5）

查看试题解析
12. 观察下列各式及其展开式：
（a+b）²=a²+2ab+b²
（a+b）³=a³+3a²b+3ab²+b³
（a+b）⁴=a⁴+4a³b+6a²b²+4ab³+b⁴
（a+b）⁵=a⁵+5a⁴b+10a³b²+10a²b³+5ab⁴+b⁵
…
请你猜想（a+b）¹⁰的展开式第三项的系数是（　　）

A、36 B、45 C、55 D、66

查看试题解析

二、填空题

13. $\sqrt{81}$ 的平方根是．

查看试题解析
14. 如图，已知 $l_{1} ∥ l_{2}$ ， $∠ 1 = 50 °$ ，则 $∠ 2 =$ .

查看试题解析
15. 在实数： $\sqrt{8} ， 0 ， \sqrt[3]{64} ， 1.010010001 ， π ， \frac{24}{7}$ 中，无理数有个.

查看试题解析
16. 将点A（-2，-3）向右平移3个单位长度得到点B，则点B在第象限．

查看试题解析
17. 如图，直线a∥b，AC⊥AB，∠1＝60°，则∠2的度数是.

查看试题解析
18. 用“*”表示一种新运算：对于任意正实数a，b，都有 $a * b = \sqrt{b} + 1$ .例如 $8 * 9 = \sqrt{9} + 1 = 4$ ，那么 $m * (m * 16) =$ .

查看试题解析

三、解答题

19.

(1)、计算： $\sqrt[3]{- 27} + \sqrt{(- 6)^{2}} + (\sqrt{5})^{2}$

(2)、已知 $(x - 1)^{2} = 4$ ，求x的值.

查看试题解析
20. 如图，已知EF∥AD，∠1＝∠2.求证∠DGA＋∠BAC＝180°.请将下列证明过程填写完整.

证明：∵EF∥AD（已知），

∴∠2＝      ▲      （                ）.

又∵∠1＝∠2（已知），

∴∠1＝∠3（                ）.

∴AB∥      ▲      （               ）.

∴∠DGA＋∠BAC＝180°（                ）.

查看试题解析
21. 在平面直角坐标系中，已知点A（－4，3）、B（－2，－3）

（ 1 ）描出A、B两点的位置，并连结AB、AO、BO.

（ 2 ）△AOB的面积是____.
（ 3 ）把△AOB向右平移4个单位，再向上平移2个单位，画出平移后的△A′B′C′，并写出各点的坐标.

查看试题解析
22. 将一幅三角板拼成如图的图形，过点C作CF平分∠DCE交DE于点F.试说明CF∥AB的理由.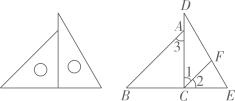

查看试题解析
23. 如图，AB∥CD，EF分别交AB、CD于点M、N，∠EMB=50°，MG平分∠BMF，MG交CD于G，求∠MGC的度数.

查看试题解析
24. 我们知道 $\sqrt{2}$ 是无理数，其整数部分是1，于是小明用 $\sqrt{2} - 1$ 来表示 $\sqrt{2}$ 的小数部分.请解答下列问题：

(1)、如果 $\sqrt{5}$ 的小数部分为a， $\sqrt{13}$ 的整数部分为b，求 $a + b - \sqrt{5}$ 的值；

(2)、已知 $10 + \sqrt{3} = x + y$ ，其中x是整数，且 $0 < y < 1$ ，求 $x - y$ 的值.

查看试题解析
25. 如图，在四边形 $A B C D$ 中， $∠ D = 100 °$ ， CA平分 $∠ B C D$ ，且 $∠ A C B = 40 °$ ， $∠ B A C = 70 °$ .

(1)、 $A D$ 与 $B C$ 平行吗？请写出推理过程.

(2)、若点E在线段 $B A$ 的延长线上，求 $∠ D A C$ 与 $∠ E A D$ 的度数.

查看试题解析
26. 如图，在长方形OABC中，O为平面直角坐标系的原点，点A坐标为（a，0），点C的坐标为（0，b），且a、b满足 $\sqrt{a - 4} + | b - 6 | = 0$ ，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O-C-B-A-O的线路移动.

(1)、a= ， b= ，点B的坐标为；

(2)、当点P移动4秒时，请指出点P的位置，并求出点P的坐标；

(3)、在移动过程中，当点P到x轴的距离为5个单位长度时，求点P移动的时间.

查看试题解析