广西壮族自治区贵港市覃塘区2021-2022学年七年级下学期期中数学试题

试卷更新日期：2023-04-13 类型：期中考试

进入出卷网下载

一、单选题

1. 下列方程中，是二元一次方程的是（）

A、 $x y = 1$ B、 $x - \frac{1}{y} = 3$ C、 $x = y$ D、 $x + y - z = 0$

查看试题解析
2. 计算（-1²）³的正确结果是（）

A、-1 B、1 C、-6 D、6

查看试题解析
3. 方程 $x - 2 y = 6$ 的解不可能是（）

A、 ${\begin{array}{l} x = - 2 \\ y = - 4 \end{array}$ B、 ${\begin{array}{l} x = 4 \\ y = - 1 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = - 2 \end{array}$ D、 ${\begin{array}{l} x = 8 \\ y = 0 \end{array}$

查看试题解析
4. 下列计算正确的是（）

A、 $3 x + 2 x = 5 x^{2}$ B、 $(- x) {(- x)}^{2} = x^{3}$ C、 $(1 - x) (x + 1) = 1 - x^{2}$ D、 ${(x - 1)}^{2} = x^{2} - 1$

查看试题解析
5. 二元一次方程组 ${\begin{array}{l} 2 x - y = - 1 \\ 4 x - 2 y = 5 \end{array}$ 的解的情况是（）

A、无解 B、只有一组解 C、有两组解 D、有无数组解

查看试题解析
6. 若二元一次方程组 ${\begin{array}{l} x - 2 y = m \\ m x + y = n \end{array}$ 的解是 ${\begin{array}{l} x = 1 \\ y = - 1 \end{array}$ ，则 $m + n$ 的值是（）

A、 $- 1$ B、1 C、 $- 5$ D、5

查看试题解析
7. 下列因式分解正确的是（）

A、 $a^{2} b - 2 a b + b = b (a^{2} - 2 a)$ B、 $- 9 + m^{2} = (- 3 + m) (3 - m)$ C、 $x^{2} - 4 y^{2} = (x + 4 y) (x - 4 y)$ D、 $x^{2} - 4 x y + 4 y^{2} = {(x - 2 y)}^{2}$

查看试题解析
8. 已知多项式 $x^{2} - x + m$ 因式分解后得到一个因式为 $x + 2$ ，则m的值为（）

A、 $- 5$ B、5 C、 $- 6$ D、6

查看试题解析
9. 若 ${(5 x + 2 y - 12)}^{2} + | 3 x + 2 y - 6 | = 0$ ，则 $x - 2 y$ 的值是（）

A、3 B、4 C、5 D、6

查看试题解析
10. 在探索因式分解的公式时，可以借助几何图形来解释某些公式.如图，从左图到右图的变化过程中，解释的因式分解公式是（）

A、 $(a + b) (a - b) = a^{2} - b^{2}$ B、 $a^{2} - b^{2} = (a + b) (a - b)$ C、 $a^{2} + 2 a b + b^{2} = (a + b)^{2}$ D、 $(a - b)^{2} = a^{2} - 2 a b + b^{2}$

查看试题解析
11. 一张方桌由一个桌面和四条桌腿组成.已知 $1 m^{3}$ 的木料可做50个桌面或300条桌腿，现用 $5 m^{3}$ 木料恰好做成若干张方桌.对于这个问题，若设用 $x m^{3}$ 的木料做桌面，用 $y m^{3}$ 的木料做桌腿，则所列方程组正确的是（）

A、 ${\begin{array}{l} x + y = 5 \\ 50 x = 300 y \end{array}$ B、 ${\begin{array}{l} x + y = 5 \\ 200 x = 300 y \end{array}$ C、 ${\begin{array}{l} x + y = 5 \\ 4 x = y \end{array}$ D、 ${\begin{array}{l} x + y = 5 \\ 300 x = 200 y \end{array}$

查看试题解析
12. 如图，在长为15，宽为12的矩形中，有形状、大小完全相同的5个小矩形，则图中阴影部分的面积为（）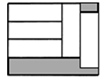

A、10 B、15 C、45 D、25

查看试题解析

二、填空题

13. 计算 $2 x^{3} \cdot {(- x)}^{4}$ 的结果是.

查看试题解析
14. 因式分解： $x^{3} - 6 x^{2} + 9 x =$

查看试题解析
15. 已知 $m + n = 3 ，$ 则 $m^{2} - n^{2} + 6 n =$ .

查看试题解析
16. 若（x-1）（x²+5ax-a）的乘积中不含x²项，则a的值为.

查看试题解析
17. 在将 $x^{2} + m x + n$ 因式分解时，小刚看错了m的值，分解得 $(x - 1) (x + 6)$ ；小芳看错了n的值，分解得 $(x - 2) (x + 1)$ ，那么原式 $x^{2} + m x + n$ 正确分解为.

查看试题解析
18. 已知关于x，y的二元一次方程组 ${\begin{array}{l} a x + 3 y = 8 & ① \\ 2 x - b y = - 3 & ② \end{array}$ ，由于甲看错了方程①中a的值，得到方程组的解为 ${\begin{array}{l} x = - 2 \\ y = - 1 \end{array}$ ；而乙看错了方程②中b的值，得到方程组的解为 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$ .若按正确的a，b值进行解方程组，则原方程组的解为.

查看试题解析

三、解答题

19. 计算：

(1)、 $- a^{2} \cdot {(- a)}^{3} \cdot {(- a)}^{4}$

(2)、 $(x - 1) (5 x + 3) - (2 x + 4) (3 x - 2)$

查看试题解析
20. 因式分解：

(1)、 $a^{2} (a - b) + 4 (b - a)$

(2)、 $m^{2} + n^{2} - 2 m n - 1$

查看试题解析
21. 解下列二元一次方程组：

(1)、 ${\begin{array}{l} 2 x + y = 4 \\ x + 2 y = 5 \end{array}$ ；

(2)、 ${\begin{array}{l} 3 x - 5 y = 3 \\ \frac{x}{2} - \frac{y}{3} = 1 \end{array}$ .

查看试题解析
22. 先化简，再求值：

(1)、 $4 a^{2} - 2 a (- a + 2 b)$ ，其中 $a = - 1$ ， $b = 2$ ；

(2)、 $(2 x - 1) (3 x + 2) - {(2 x - 3)}^{2}$ ，其中 $x = - \frac{1}{2}$ .

查看试题解析
23. 已知：关于x，y的二元一次方程组 ${\begin{array}{l} 2 x - y = a + 6 \\ x + 2 y = 2 a - 8 \end{array}$ 的解满足 $x + y = a$ ，求 $x^{2} - y^{2}$ 的值.

查看试题解析
24. 根据已知条件，求代数式的值：

(1)、已知 $m + \frac{1}{m} = 3$ ，求 $m^{2} + \frac{1}{m^{2}}$ 的值.

(2)、已知 $a - b = 3$ ， $a b = 2$ ，求 $a^{4} + b^{4}$ 的值；

查看试题解析
25. 亚洲文明对话大会召开期间，大批的大学生志愿者参与服务工作.某大学计划组织本校全体志愿者统一乘车去会场，若单独调配36座新能源客车若干辆，则有2人没有座位；若只调配22座新能源客车，则用车数量将增加4辆，并空出2个座位.

(1)、计划调配36座新能源客车多少辆？该大学共有多少名志愿者？

(2)、若同时调配36座和22座两种车型，既保证每人有座，又保证每车不空座，则两种车型各需多少辆？

查看试题解析
26. 实践操作，解答问题：在一次数学实践活动中，某兴趣小组用边长分别为a和b的两种正方形纸片进行拼接操作，其中 $a > b > 0$ ， $a < 2 b$ .
操作一：取两种正方形纸片各一张按如图①所示放置，将图中没有叠合部分（阴影）的面积记为 $S_{1}$ ；
操作二：取一张边长为a的正方形纸片和两张边长为b的正方形纸片按如图②所示放置，将图中两张边长为b的正方形纸片重叠部分（阴影）的面积记为 $S_{2}$ ；
操作三：取两种正方形纸片各一张按如图③所示放置，将图中阴影部分的面积记为 $S_{3}$ ；

(1)、用含a，b的式子分别表示 $S_{1}$ 和 $S_{2}$ ；

(2)、若 $a + b = 10$ ， $a b = 23$ ，求 $S_{1} + S_{2}$ 的值；

(3)、当 $S_{1} + S_{2} = 30$ 时，求 $S_{3}$ 的值.

查看试题解析