沪科版数学八年级下册第17章一元二次方程基础过关单元卷

试卷更新日期：2023-04-13 类型：单元试卷

进入出卷网下载

一、单选题（每题4分，共40分）

1. 下列方程是一元二次方程的是（）

A、 $x^{2} + x - y = 0$ B、 $a x^{2} + 2 x - 3 = 0$ C、 $x^{2} + 2 x + 5 = x (x - 1)$ D、 $x^{2} - 1 = 0$

查看试题解析
2. 用配方法解一元二次方程 $2 x^{2} - 7 x + 6 = 0$ ，下面配方正确的是 $($ $)$

A、 $(x - \frac{7}{4})^{2} = \frac{1}{16}$ B、 $(x - \frac{7}{4})^{2} = \frac{97}{16}$ C、 $(x - \frac{7}{2})^{2} = \frac{37}{4}$ D、 $(x + \frac{7}{4})^{2} = \frac{1}{16}$

查看试题解析
3. 对于方程x²＋bx－2＝0，下面观点正确的是( )

A、方程有无实数根，要根据b的取值而定 B、无论b取何值，方程必有一正根、一负根 C、当b>0时，方程两根为正；b<0时．方程两根为负 D、∵－2<0，∴方程两根肯定为负

查看试题解析
4. 已知 $x_{1}$ ， $x_{2}$ 是关于 $x$ 的方程 $x^{2} - x - 2023 = 0$ 的两个根，则 $x_{1}^{2} - 2 x_{1} - x_{2}$ 的值为（）

A、2023 B、2022 C、2021 D、2020

查看试题解析
5. $x = \frac{2 \pm \sqrt{{(- 2)}^{2} - 4 \times 3 \times (- 1)}}{2 \times 3}$ 是下列哪个一元二次方程的根（）

A、 $3 x^{2} + 2 x - 1 = 0$ B、 $2 x^{2} + 4 x - 1 = 0$ C、 $- x^{2} - 2 x + 3 = 0$ D、 $3 x^{2} - 2 x - 1 = 0$

查看试题解析
6. 已知关于x的一元二次方程kx²﹣（2k﹣1）x+k﹣2＝0有两个不相等的实数根，则实数k的取值范围是（）

A、k＞﹣ $\frac{1}{4}$ B、k＜ $\frac{1}{4}$ C、k＞﹣ $\frac{1}{4}$ 且k≠0 D、k＜ $\frac{1}{4}$ 且k≠0

查看试题解析
7. 若两个连续奇数的积为63，则这两个数的和为（）

A、16 B、17 C、±16 D、±17

查看试题解析
8. 随着“二胎政策”出生的孩子越来越大，纷纷到了入学年龄，某校2021年学生数比2020年增长了8.5%，2022年新学期开学统计，该校学生数又比2021年增长了9.6%，设2021、2022这两年该校学生数平均增长率为x，则x满足的方程是（）

A、 $2 x = 8.5 % + 9.6 %$ B、 $2 (1 + x) = (1 + 8.5 %) (1 + 9.6 %)$ C、 $2 {(1 + x)}^{2} = (1 + 8.5 % + 9.6 %)$ D、 ${(1 + x)}^{2} = (1 + 8.5 %) (1 + 9.6 %)$

查看试题解析
9. 一个等腰的底边为4，腰是方程 $x^{2} - 5 x + 6 = 0$ 的一个根.则这个等腰三角形的周长可能是（）

A、8 B、10 C、8或10 D、9

查看试题解析
10. 如图，在活动课上，老师画出边长为2的正方形ABCD ，让同学们按以下步骤完成画图：
⑴画出AD的中点E ，连接BE；

⑵以点E为圆心，EB长为半径画弧，交DA的延长线于点F；

⑶以AF为边画正方形AFGH ，点H在AB边上．在画出的图中有一条线段的长是方程x²+2x﹣4＝0的一个根．这条线段是（）

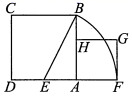A、线段BH B、线段BE C、线段AE D、线段AH

查看试题解析

二、填空题（每空5分，共25分）

11. 已知： $(m - 1) x^{| m + 1 |} + 6 x - 1 = 0$ 是关于x的一元二次方程，则m=.

查看试题解析
12. 已知m是方程 $x^{2} + 2 x - 1 = 0$ 的一个根，则代数式 $2 m^{2} + 4 m + 2021$ 的值为

查看试题解析
13. 关于x的一元二次方程 $x^{2} + 2 x + t = 0$ 有两个相等的实数根，则实数t的值为.

查看试题解析
14. 如图，用120米长的围网围建一个面积为560平方米的矩形养殖场．为了节省材料，养殖场的一边靠墙（墙足够长），并在如图的两个位置各开出一个1米宽的门（门不用围网做）．设矩形AB边长为x米，请依题意列方程：．

查看试题解析
15. 如图，在 $R t Δ A B C$ 中， $∠ C = 90 °$ ， $A C = 30 c m$ ， $B C = 21 c m$ ，动点 $P$ 从点 $C$ 出发，沿 $C A$ 方向运动，动点 $Q$ 从点 $B$ 出发，沿 $B C$ 方向运动，如果点 $P$ ， $Q$ 同时出发， $P$ ， $Q$ 的运动速度均为 $1 c m / s$ ．那么运动秒时，它们相距 $15 c m$ ．

查看试题解析

三、计算题（共2题，共20分）

16. 解方程：

(1)、 $y^{2} - 7 y + 6 = 0$

(2)、 ${(x - 1)}^{2} = {(3 x - 4)}^{2}$

查看试题解析
17. 解方程：

(1)、3x²-5x+1=0（配方法）；

(2)、(x+3)(x-1)=5（公式法）．

查看试题解析

四、解答题（共6题，共65分）

18. 已知关于x的一元二次方程x²＋（2m﹣3）x＋m²＝0的两个不相等的实数根α，β满足 $\frac{1}{a}$ ＋ $\frac{1}{β}$ ＝1，求m的值．

查看试题解析
19. 已知 $x_{1}$ 、 $x_{2}$ 是关于 $x$ 的一元二次方程 $x^{2} - 2 (m + 1) x + m^{2} + 3 = 0$ 的两个实数根.

(1)、求 $m$ 的取值范围；

(2)、是否存在实数根 $m$ ，使 $(x_{1} - 1) (x_{2} - 1) = m + 6$ 成立，若存在，求出 $m$ 的值，若不存在，请说明理由.

查看试题解析
20. 有两个人患了流感，经过两轮传染后共有242人患了流感.

(1)、每轮传染中平均一个人传染了几个人？

(2)、若一个患流感的人打一个喷嚏喷出的病毒粒子（忽略触角近似于球体）达8000万个，且该流感病毒粒子的直径为160纳米.请完成下列填空及问题：
①用科学记数法表示数据8000万个为个；

②如图，若把8000万个病毒粒子最大纵切面圆面相切放在一条直线上，求这些病毒粒子纵切面的总直径是多少米？（参考数据：1纳米 $= 1 0^{- 9}$ 米）

查看试题解析
21. 如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 12 c m$ ， $B C = 24 c m$ ，动点 $P$ 从点 $A$ 开始沿边 $A B$ 向点 $B$ 以 $2 c m / s$ 的速度移动，动点 $Q$ 从点 $B$ 开始沿边 $B C$ 向点 $C$ 以 $4 c m / s$ 的速度移动，如果 $P$ ， $Q$ 两点分别从 $A$ ， $B$ 两点同时出发，设运动时间为 $x$ $s$ ．

(1)、用含x的式子表示：
$A P =$ $c m$ ，

$B P =$ $c m$ ，

$B Q =$ $c m$ ，

(2)、当 $△ P B Q$ 的面积为 $32 c m^{2}$ 时，求运动时间；

(3)、四边形 $A P Q C$ 的面积能否等于 $172 c m^{2}$ ？若能，求出运动的时间；若不能，说明理由．

查看试题解析
22. 2022年北京冬季奥运会于2月4日至2月20日在北京市和河北省张家口市联合举行，冬奥会吉祥物为“冰墩墩”.

(1)、据市场调研发现，某工厂今年二月份共生产500个“冰墩墩”，为增大生产量，该工厂平均每月生产量增长率相同，四月份该工厂生产了720个“冰墩墩”，求该工厂平均每月生产量增长率是多少？

(2)、已知某商店“冰墩墩”平均每天可销售20个，每个盈利40元，在每个降价幅度不超过10元的情况下，每下降2元，则每天可多售10件.如果每天要盈利1440元，则每个“冰墩墩”应降价多少元？

查看试题解析
23. 定义：已知 $x_{1} ， x_{2}$ 是关于x的一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 的两个实数根，若 $x_{1} < x_{2} < 0$ ，且 $3 < \frac{x_{1}}{x_{2}} < 4$ ，则称这个方程为“限根方程”.如：一元二次方程 $x^{2} + 13 x + 30 = 0$ 的两根为 $x_{1} = - 10 ， x_{2} = - 3$ ，因 $- 10 < - 3 < 0$ ， $3 < \frac{- 10}{- 3} < 4$ ，所以一元二次方程 $x^{2} + 13 x + 30 = 0$ 为“限根方程”.
请阅读以上材料，回答下列问题：

(1)、判断一元二次方程 $x^{2} + 9 x + 14 = 0$ 是否为“限根方程”，并说明理由；

(2)、若关于x的一元二次方程 $2 x^{2} + (k + 7) x + k^{2} + 3 = 0$ 是“限根方程”，且两根 $x_{1} 、 x_{2}$ 满足 $x_{1} + x_{2} + x_{1} x_{2} = - 1$ ，求k的值；

(3)、若关于x的一元二次方程 $x^{2} + (1 - m) x - m = 0$ 是“限根方程”，求m的取值范围.

查看试题解析

沪科版数学八年级下册第17章 一元二次方程 基础过关单元卷

一、单选题（每题4分，共40分）

二、填空题（每空5分，共25分）

三、计算题（共2题，共20分）

四、解答题（共6题，共65分）

沪科版数学八年级下册第17章一元二次方程基础过关单元卷